Month: November 2008 (page 1 of 1)

November 28, 2008 / 0 Comments

Tips for keeping your digital self organized using Google applications and services

In today’s modern world, teachers are faced with an ever more difficult task of keeping their resources and their lives organized. It feels like greater demands are being expected from teachers and that our job is becoming more difficult. Here are some simple things you can do to both keep yourself more organized, and in the long run save yourself a lot of time.

Google has a number of wonderful applications, and I’m going to talk about a couple of them in a bit of detail here because they will help you immensely, once you know their power. I have been using the calendar application provided by Google for a year and a half now, quite successfully, to both store my lesson plans, and keep track of my schedule. The other application I use multiple times daily is Gmail.

It has a number of important features that I should mention. The first is that you can have as many calendars as you like, and switch the display between the calendars. This allows you to, for instance, share a calendar with someone else and overlay your calendars to find a common meeting time by looking for the places where neither of you have something scheduled. It also allows you to edit a private calendar and then easily switch to editing a public calendar. Another nice feature is the ability to subscribe to your calendar and receive daily reminders about what you have planned for the day in email form.

The best feature of the Google calendar, in my opinion, is the ability to set it as either private or public. When your calendar is private, you can invite individual people to view your calendar, but otherwise it remains hidden from the public. My wife is subscribed to my calendar and I to hers, and we can share information between the two of us pretty easily. However I also have a public calendar I’ve created and I provide a link on my class blog so the students can see the calendar.

As for Gmail it has a number of cool features. The interface is extremely easy to use, and includes useful features like creating automatic filters for your incoming email messages, labelling conversations to make them easier to find in the future, and built in chat with other Gmail users. You can also add widgets to your Gmail page, like for example embedding a display of your personal Google calendars or a comic of the day application. The size allocated to you is gigantic at over 7 gigabytes of space and counting. I almost never delete any of my messages, and with their custom "Search your mail" feature, you’ll never lose an email again.

Both of these applications work together to provide you much of the power of Outlook on Windows, but accessible from anywhere you have an internet connection. As well, I am fairly sure you can access these two applications from your iPhone or Blackberry, and I have some seen tutorials on keeping your portable information devices synced with your Google applications. These two applications together can save you a lot of time and effort keeping track of information you have received and things you have to do.

I’ve been using Google Sites with my students on a recent project, and it is a very easy way to create a website, either for personal or professional use. You can easily create multiply web sites, and invite students (or anyone with an email address) to help you build a site, while keeping your other sites separate. As well, each site can individually be set to be publically viewable, or viewable by invite only.

In your Google sites you can embed pictures, videos, and Google calendars. This gives you an easy way to take the calendar you created using Google calendar and display it for your students, allowing students and parents to view your school schedule. Saves a lot of time when negotiating with your students about when to meet them for extra tutoring.

Try out these web applications sometime. Trust me, you won’t regret it.

November 24, 2008 / 4 Comments

Ways to use Geogebra in a mathematics classroom

There are a lot of good open source programs out there, but not many of them have direct application to a mathematics classroom the way Geogebra does. Geogebra is a software package for creating and manipulating geometric objects. It also allows for graphing of funcitons and manipulating the functions in all sorts of interesting ways. It runs on the Java framework, which means if you have Java installed on your computer, you can run Geogebra, which makes it any Java enabled operating system. This means the very same program will run on Windows, Mac, Linux or Solaris, although the installer is different for each operating system.

If you are planning on using the program with your students, it is nice to know that they can install the program for free, and that it is very likely to work on their computer. The only caveat is that you need to make sure the students have the right version of Java installed if they have any problems as this can sometimes be an issue.

Geogebra has all of the standard Geometry software functions. You can add lines, circles, ellipses and all other sorts of geometric functions to the document. You can also make one object a dependent of another object which means that changes in the original object propagate to its dependent objects. So in other words, if a you draw a line segment which depends on the location of point A and point B, changing either point A or point B modifies the line segment.

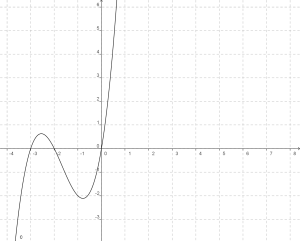There are 2 cool things I like about Geogebra. The first is that you can export your working file as a dynamic worksheet on a web page, which means you can easily make what you are working on web ready. The second feature which I use all of the time is the ability to export my current file as a picture in PNG (and a few others) format. This allows me to use Geogebra to create graphs for inclusion in my online posts, something my students and I use Geogebra for all the time.

Geogebra also has an input textfield, which means that every command you can use the interface to enter, you can also type in. Some commands are done much more easily through the input textfield, things like entering y = x^2 + 3x which uses the nature notation to graph a function. Entering Function[x^2, 0, 2] graphs the function over the domain from 0 to 2 for x. Very handy.

Using Geogebra with your classroom is an affordable way to bring high quality geometry software to your classroom at an extremely affordable price (its free!!). I’ve only scratched the surface of what Geogebra is capable of doing, I suggest you try it out yourself. Maybe when I have time I’ll create some tutorials on using it.

November 23, 2008 / 0 Comments

Resource sharing between teachers.

As part of my Masters degree, I have created a venture pitch for a project I am working on called Pedagogle.com. Our assignment was to create a pitch as if we are the CEO of an organization which is looking for venture capital. We are essentially creating our own start up idea, and then learning how to create a pitch to market our idea.

The process has been quite fun, although I have found myself wading through problems editing the video, and getting the quality of the video high enough to make it worth watching. I tried unsuccessfully many times to convert it into FLV format to reduce the size of the file a bit, but found the quality degraded too much to make it worthwhile. So I gave up, and settled on both embedding the file within a page, and providing a link to download the file as an AVI. Hopefully everyone can figure out a way to watch the pitch. Unfortunately this means the file size is sitting just under 50 MB which is pretty large. I’m not going to want to host this myself for too long…

The idea of my pitch is to introduce how organization of information has evolved over time and to place Pedagogle as a logical step in that process. As I go through the pitch I introduce some benefits of Pedagogle, but am mostly focussing on the organizational benefits as I see those as the most important reasons why a teacher might want to use this resource.

On the page where my venture pitch begins, I describe some other reasons for using my service, including the fact that other people will use it which improves the pool of available resources and that your resources are automatically backed up for you, reducing the likelihood of computer malfunction costing you hundreds of hours of work.

Anyway, check out the pitch and the site, Pedagogle.com and let’s see if we can make a difference in the lives of educators.

November 22, 2008 / 0 Comments

Formatting mathematics equations online

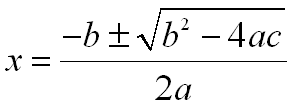One difficulty faced by any mathematics teacher who wants to present material online is formatting of their documents. Ideally, you’d like to be able to add equations to your online documents as easily as you can to Microsoft Word. Unfortunately, this is not the case.

Over the past three years, I have researched a number of options. There are no simple solutions to this problem, just solutions with varying degrees of difficulty. A number of these solutions are within reach for your students to use as well, should your students be involved with any of your online projects.

The simplest solution I have found is unfortunately using a propietary program. Basically the steps are as follows. You open up Microsoft Word, and confirm you have the bundled Equation Editor installed. This is likely to be true in Word 2003, and virtually assured in Word 2007.

Basically the steps are as follows. You create the equation using Equation Editor. It really is one of the easiest programs to use. Unfortunately, in both 2003 and 2007, the equation is not immediately an image, it is and object in a Word document, so you need to find a way to export it out of the program. If you are using 2003, what you basically create a screen-shot of what appears in your monitor, and paste the result into a simple image editor. Crop the screen-shot appropriately, save it as a file, and you are good to upload your image for insertion into your online document. In 2007 you don’t need to create a screen-shot, you can just go to File ⇒ Save As ⇒Word 2003. Microsoft Word automatically converts all of the equations in your document to images, which you can then Copy and Paste into some image editing software one at a time and save as pictures.

The benefit of this process is that the creation of the equations is relatively straight forward. However, this process is a bit tedious especially if you have a lot of equations to produce.

Another option is to create the equations is to use an online equation editor such as the one available at http://www.sitmo.com/latex/. This allows you to enter in LaTeX and produce an image of your equation. So you enter the very cryptic x = \frac {-b \pm \sqrt{b^2-4ac}}{2a} and it turns it into the equation . Fortunately on the page in question their editor allows you to modify the LaTeX using some buttons, which simplifies the process. You can also preview the result of your LaTeX to make sure it is correct. You then save the resulting preview image to your computer, and upload and insert it into your post.

There are two problems with this solution. The first is that if Sitmo goes out of business, you lose the ability to add equations in this manner. The second problem is that you again, have to create each equation one at a time, and upload them one at a time to your online document. The benefit of this solution is that it doesn’t require you to install any software and will work on any computer, anywhere.

A third solution is to host your own CGI on your server to convert your own LaTeX that you type into your interface to create the documents, and it is converted automatically into an equation image for you. This is ideal, except that whether or not it works depends a lot on your server set up, and what content management system you are using. For Drupal there is a module you can add which does this, called Mathfilter which I know works, since I wrote the module. You can use it, and apply a patch suggested by one of the Drupal developers, to produce very similar equations. [tex]x = \frac {-b \pm \sqrt{b^2-4ac}}{2a}[/tex] becomes $x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}$ using the filter.

The problems with this 3rd solution are numerous which essentially all boil down to needing some technical expertise to install the system, and needing knowledge of LaTeX to use it. The benefit is, you become in charge of when and where you insert equations into your documents, and you can insert them on the fly as you create your document.

Whatever method you choose, it is clear that including mathematical equations online is feasible, even if none of the solutions is really mature.

November 20, 2008 / 2 Comments

Working with a 1 to 1 laptop program

At our rather large high school in Thailand, we have a 1 to 1 laptop program. Every student in the high school has a laptop, which they are supposed to bring to class. After a year and half working with these laptops, I discovered the joys and pitfalls of such a system.

The really nice thing about the laptops is that you can plan activities that require a computer much more easily than schools where you have to book time in a computer lab. Having done both, the laptops are just plain easier to work with.

Another advantage of the laptop program is that a greater percentage of the students you work with have an intermediate level understanding of how their computers work. They can manage their documents in a relatively organized fashion, install software, navigate the web, and use a search engine, all with relative ease. It has been very rare when I have not been able to explain to one of my students how to accomplish a task. I find myself being able give instructions to the students using higher level skills and more complicated phrases than my previous school.

For example, I can tell the kids to ‘copy and paste’ and to ‘create a screen-shot’ and most of the kids know how to do this stuff. I can also give instructions like ‘copy the URL for the image and paste it into the textfield on the image uploader’ and they can do it.

Another nice feature of the 1 to 1 laptop program is that it allows me to include a little bit of tech training in my lessons. Since it is likely that the students will be using a computer pretty regularly for the rest of their lives, it seems to me that the use of a computer is one of the most important skills I can pass along to my students.

Since the students have access to a computer at any time, you can use a number of online tools quite effectively. I have mentioned in a previous article about using Google Docs for collaboration online, and with my classes I have also successfully used blogs, wikis and other resources I have found online with my students.

There are a number of problems with the use of the laptops however which need to be pointed out.

The first problem is that if you plan a lesson that involves everyone needing a laptop and one or more students does not have their laptop, you can find yourself going to your backup pretty quickly. Students have difficulty keeping their laptops virus clear because of all of the file sharing they do. They also sometimes just forget their laptops at <insert the location here>.

Another problem, at least at our school, is that there seem to be some limits as to how many students can access a wireless acccess point at the same time. So once the first 15 or so students in your class get started, the next 5 or 10 students are locked out. This can be pretty frustrating pretty quickly.

Students will also tend to use their laptops for inappropriate things during your lessons. The student in the back that you think is diligently using their laptops for taking notes is probably text chatting with their friend in Physics or Biology. Students who are supposed to be carefully working from a PDF version of their textbook are actually surfing blogging sites looking for next year’s fashion. This can be real problem, and as usual you need to rely on your own classroom management skills to try and curb this kind of behaviour. Some schools install special software on the network server to limit students access to the internet, but the kids in your class will probably just turn to computer games instead.

When all is said and done, I have enjoyed the access to a 1 to 1 laptop program I have had at my current school. There have been some problems, but they have not been insurmountable. It is likely that more and more schools will be looking to initiate similar programs, so we as educators must prepare for the future.

November 19, 2008 / 1 Comment

Making mathematics fun

One major barrier to students learning mathematics is that they spend a lot of time NOT enjoying themselves. Let’s be honest, listening to poetry is enjoyable if the poetry is selected carefully. Having discussions about current events in History, while learning critical analysis skills, is fun. Solving a cubic equation is just not a lot of fun, even for mathematicians.

We as mathematics educators are charged with the job of making math accessible and more easily learned by our students. It makes sense therefore to inject a bit of fun in once in a while, especially if you can justify it with some educational theory that suggests it is pedagogically worthwhile.

Trebuchet project A project I have done with my 9th grade students now for 4 years in a row, is to have them do some quadratic modelling. When I worked in London, I was really lucky because the students were creating trebuchets and catapults in their Design class. So we had a class where the students took their models they created in Design up to the nearest park, and we took digital footage of the trebuchets in action.

At the end of the period, when the students had enough footage, they submitted some samples of their models at work in digital form directly to my computer, and that night I converted their video to a usuable form. This actually meant I spent hours figuring out how to convert all of their wacky video formats into something readable by the FFMPEG converter to an flv file, which I could then set up to stream.

There were some technical difficulties which some of the groups had. For example, one of the groups decided to do their footage from 20 metres away with no background…their poor little golf ball wasn’t very visible in their footage. Another group videographer had a very unsteady hand. However, I ended up with 6 good videos, so I split the students into 6 groups and they went to work analyzing their footage the next class.

Students had to figure out a way to convert the flight of their ball into coordinates, in other words numerical data. They then had to decide on a model for their data, and find an equation to represent it. I also had them calculate the mean horizontal speed (which involved being able to convert frame rates into an appropriate unit of time). Finally there were some questions the students had to include in their write-up for this projectto focus their thinking on the physical phenomena that happened.

What was wonderful about this experience is the reaction of the kids. At all stages of the project they were all actively engaged and interested in what they were doing. The mathematics, which could have been very dull and boring for them came alive.

Just listen to the reaction of the students in the video when their trebuchet goes off for the first time. How often do you get to hear a spontaneous cheer in a mathematics class?

November 16, 2008 / 2 Comments

Using a class blog effectively

Something I have been doing for the past three years now is using a blog with my classroom. I have developed my practices with the blog over time and so far here are some of the things I have been doing with it.

The first thing for which I used my blog was to distribute information to the students, and provide announcements for the class. Some of the things I might announce would be dates of upcoming tests, due dates for assignments, and upcoming topics. I also used the blog originally as a way to provide links for resources, intended to be used in class. This way students would not have to type in any lengthy URLs and could just click to get straight to the online resource. Occasionally I would also upload a file to our class blog and expect the students to be able to download it for access.

Now that I have been using a blog with my classroom for a few years, I have found some more sophisticated ways of using it, which I want to discuss here.

One immediate change I made was to transfer the load of publishing to the blog with my students. In the first year that I tried this, what happened was that one of my classes, an advanced grade 10 math class, posted daily summaries of what happened in class to the math blog. This responsibility rotated around the class and when each student had posted their blog, they chose the next person.

This worked reasonably well, since occasionally students would come to class with questions they had discovered when reading the blog. They would also occasionally comment on each other’s summaries and I hope that most of the students read each other’s posts.

The next step I took was logical, having tested out blogging with a class, I decided to try it with all of my classes. I actually took the time to install the blogging software myself, hosted on my school’s server, so that I would have greater control over the process. I wanted to be able to easily administrate the students’ accounts and be able to assist them with common problems, like forgetting their passwords. I also made sure that posting to the blog was a part of the students’ grades, given its growing importance.

As soon as I did this, it became clear to me that not all of my students were reading the blog on a regular basis. So this year I implemented another change, students would be marked on their full participation in the classroom blogging. Not only would they be rotating through responsibility for creating summaries of that day’s class, they would have to post comments on the summaries for other student’s summaries. This way I could guarantee that students were at least reading each other summaries. The comments students have produced have mostly been really appropriate and high quality.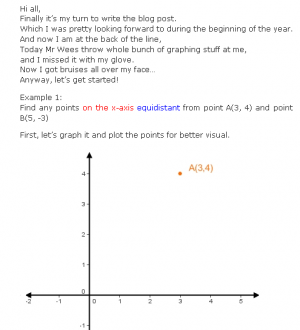

When I added the commenting on each other’s posts, something fascinating happened. The quality of the blog summaries improved. Students were aware that I grade the quality of the blog, but that I use a pretty forgiving rubric. If students complete their summary, and it makes sense, they get full marks for participation. What has obviously driven the improvement in their posts has been the awareness that their peers are reading them.

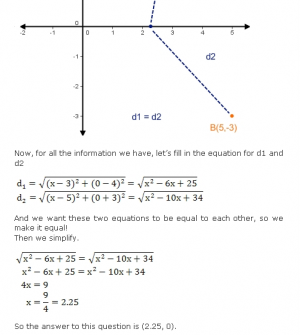I think a second driving factor in the improvement in the quality of the posts has been a bit of competition, particularly among the stronger mathematics students. They are basically competing to see who can create the best post.

Some of the posts, especially recently have been exceptional. Students have become more comfortable with the format and are incorporating humor and more media into their posts. Graphs and properly formated equations have almost become an expectation for their posts.

The ways students have been creating the graphs and equations have been quite creative. Some students find images from other websites online, and use these instead. Some students take the time to create their images instead using programs like Microsoft Paint, Adobe Photoshop, and Geogebra. For the creation of the equations, most students have been using my built in Equation parser (which means learning a little bit of Latex). The equations shown in the pictures here are actually created in Microsoft Word, and then exported to pictures using a lengthy process.

I’m not sure what the next step is. I know I need to collect some information. At some point near the end of the semester, I plan on collecting some anonymous data from the students to try and answer the following questions.

How long, on average, does it take you to create a summary?
How often do you check the blog to see if any new summaries are up?
Do you read the summaries from any of the other classes?
Have you felt any of the comments have been too critical?

In summary, blogging with your students as a class can be an effective way to increase their retention of your material. They may end up learning some of the material from their peers because of the differences in how it is explained. Your students will also end up having to view your classroom material in a different format, so it will activate a different part of their brain, and so some students will benefit from this experience (think Howard Gartner’s multiple intelligences). Your students will also be likely to learn some valuable technical skills from the experience. Finally, your students may just enjoy the experience, which will make them enjoy (and remember) your class for a bit longer.

November 15, 2008 / 2 Comments

Using Google Docs when teaching mathematics

Google has a lot of cool tools they have been working on recently, and I enjoy trying them out. Once in a while they come up with a tool you can use in your classroom right away.

One of the tools we are using in my classroom right now is Google Docs. This is an online document collaboration tool which allows people from anywhere, using most modern browsers to upload, edit, and share documents online. It supports many different formats, and you can export the document and download it at the end if you finish working on it.

I have been using it as a place for my students to share their workload. I created 12 Google Documents, 1 for each of 12 groups in 2 different classes. I then collected the email addresses of my students and assigned them to groups of 3. I went through each of the 12 documents and used the ‘Share’ feature of Google docs to allow the students to collaborate on the each document as well.

One caveat I discovered is that if the student’s email address is not a Google mail account, they need to verify their account. Unfortunately this verification process takes about an hour of real time, presumably as Google syncs up the account verification across their many, many servers. There are two solutions to this. The first is to make sure you have the students do the account verification a day before you actually want them to use the documents. The second solution is to have the students sign up for Google mail accounts first, and then send them invitations to their groups.

To be honest, mathematics as a subject is not especially suited for online collaboration. This is because the creation of equations can be a bit tricky for the uninitiated. There are a number of solutions for creating professional equations online, which all have their benefits and drawbacks.

The first and easiest solution for the students is to use Microsoft Word and create their equations in Equation Editor (or if you can afford it the far superior Mathtype). The only problem here is that the kids think they can copy and paste the equations into their documents, which of course doesn’t work. The second problem is that if you ‘Import’ a document (another feature of Google Docs), your equations don’t make it. Ugh. The work around for me was to have the students take screen-shots of their equations in Word, and then crop the screen-shots in an image editor program (like Microsoft Paint). I’m not normally a huge fan of Microsoft programs, but their Equation editor really is one of the best tools for easily creating equations I’ve seen.

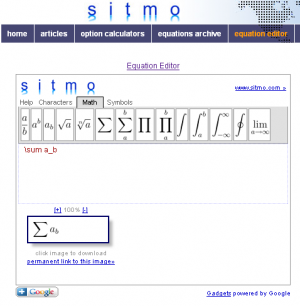The second solution is to use one of the online services offered to use the Latex document format and an elaborate system to convert the Tex documents produced into equations. The one I like best right now is offered by www.sitmo.com. You basically create the Latex, which is made easier using the editor above, and you can immediately preview the results. Underneath the preview image there is a link, which the students can right-click and ‘copy link location’. Once they have the link to the image, they go back to the ‘Insert => Image’ offered by Google Docs and paste the link into the textfield provided. I have been teaching my high school students some Latex and they have picked up the simple things pretty quickly.

Formating the text otherwise in the editor is relatively straight forward, it feels similar to how you format text in most word processing programs, which maybe a few less options. What’s brilliant about this system is that each student can be editing exactly the same document online at the same time! You can also be sitting at your desk with all of the documents open and see the students editing the document. This means a little bit less concern about students messing around while accessing the internet, which is always a huge problem in a 1 to 1 computer set up.

The other handy feature is the ‘View revisions’ tool which allows you to see what changes have occurred to the document over time. I use this to see who added what to their projects and to make sure that each student contributes at least approximately equal amounts to their projects.

When the students are done working on their document, you can just go and look at it online and grade it. No need to print out the document, but if you feel the need you can download it in your format of choice and then print it out. They have a print directly feature as well, but I have found the output varies greatly depending on your browser.

Deciding what kinds of projects are appropriate for this kind of collaboration can be a bit tricky. I am currently using it for my students to produce sample projects for their International Baccalaureate (IB) Mathematical Studies course so they have a bit more practice before they have to do the real thing. What you decide to use it for is up to you, but note that some of the problems (like inserting equations or graphs) don’t happen in other subject areas, so this technique might be even more useful in an English class, for example.

November 14, 2008 / 0 Comments

What can I do to help my child learn mathematics?

Update: It’s amazing how much my thinking has changed since I wrote this post. I literally cringed as I read the part about homework & test scores.

One of the most common questions I am asked by parents during parent teacher conferences is, what can I do to help my child learn mathematics? There are a variety of answers I can give to this question.

The very first thing you can do is have a positive attitude about mathematics. Almost anyone I meet who does not use mathematics for their career tells me how hard they found it, or how much they dislike mathematics. Your positive attitude about mathematics will rub off on your child and will help encourage them to keep trying.

Show an interest in what your child is learning. Find out what they will be learning this year in mathematics and keep track of where they are at. There are certain topics that everyone finds more difficult, make sure your child has the help they need for those topics. If you move from one school to another, this information will help your son or daughter adjust to their new mathematics class.

From an early age, encourage your child to think about puzzles and problems. Having an active imagination and a willingness to think carefully are two huge assets when doing mathematics. Many times students struggle with mathematics because they do not know how to persevere.

Work with your child on their homework whenever possible. This does not mean do their homework, it means help them finish it. There is a clear relationship between finishing their homework and your child’s scores on classroom tests and assignments.

Make sure your child has their addition and multiplication tables memorized. This can be very difficult for some children, but it is one of the few things that really should be learned by repetition. Not having to use their calculator for every single calculation will speed up how quickly your child can work, which will lead to improved test scores.

Keep in touch with the person who teaches your child mathematics. Make sure you are communicating with them often so that you are aware of your child’s progress in mathematics. Strong communication between parents and teachers helps improve students’ progress.

Most of mathematics is interrelated. There are connections between different topics which can sometimes be missed by students. If you send your child to Kumon math, or something similar, you should be aware that these connections are not taught in these types of classes. This time would be much better spent having your child work with a private tutor in mathematics.

Be realistic in your expectations. Not every person is a mathematician, and therefore not every child will be a mathematician, but all children can experience success in math class with sufficient support. Give encouragement when your child improves rather than discouraging them when they do poorly. Set reasonable goals for your child to achieve and give rewards for their achievement. An expression used often in North America is “you catch more flies with honey than with vinegar” which basically means that rewards are more effective than punishments.

If you follow these guidelines, your child should have a rewarding experience in mathematics. Remember that the goal of a mathematics class is to encourage analytical thinking and problem solving skills. If at the end of your child’s school career they are a critical thinker, and are willing to tackle challenging problems, then you have done a good job.

November 14, 2008 / 0 Comments

Helping students produce effective high quality projects

As secondary mathematics becomes more and more about how you find the solution to a problem and less about what the correct answer is to a problem, it becomes easier to justify assessing students using a project.

One immediate advantage of doing projects in high school mathematics is that students learn valuable job related skills, such as formatting documents properly, technical writing, and communication skills. It is arguable that these skills are more important than the actual mathematics content we teach.

So now it becomes a question of helping students produce high quality projects that are worth your time to grade. We as professionals need to come up with some strategies for helping our students through these projects, because if done correctly, they can be far more difficult than our most challenging topics in mathematics.

First, when assigning the project, it is helpful if you have taken the time to do it yourself. Make sure that whatever work you are planning on giving the kids has a clear solution, and that the students in your class are capable of finding it. This does not mean that your project can’t be open-ended, but students need to have some measure of success when working on the project. I have made the mistake in the past of assigning a project which was much too difficult for my 10th grade students to do, and regretting it in the end. No real learning comes from doing a project which is beyond your talent to complete.

The next thing to consider when assigning the project is the clarity of your instructions. The first few projects you assign should be pretty doable by the students by following your instructions verbatim. Give the students a formalized structure to follow. It is a good idea to even give the students a template to follow. This does not mean a ‘fill in the blanks’ style assignment, but more like giving them the following structure.

Sample project structure

You also need to give the students the same assessment criteria you will be using to grade their projects before they start working on them. A rubric is a handy way to grade a project, so give the students a copy of the rubric you will use. Take the time to go through the rubric, and if the project is one you have done before you might even be able to show some examples from a previous year.

Now you need to set aside at least a couple of lessons during class for the students to work on their projects. Once the students have started on their projects and have some work, they will want to finish the projects. They will come to you and ask for more help, but you have to give them enough time to get ‘hooked’ into the project. Sometimes what I will do is have students collect data on some phenomena in groups, and then they work on the calculations, conclusion and evaluation of their projects individually.

Give the students enough time to finish the projects before expecting them back. You can have a project that takes the students three weeks to finish, if you provide daily reminders of the tasks that need to be completed. You may also want to set goals for the students to reach and remind them what stage of the project they should be at in order to complete it on time.

If the students turn in work, and it is not as high quality as you would like, take the time to analyze the work as a class. Maybe photocopy some of the best and worst work, making sure to obscure who’s work it is (retype it if you have to) and hand it out to the students. Discuss with the students what worked and what did not. Let the students redo their assignment if they have to and turn it back in. Remember that your objective is to have the student capable of producing a high quality piece of work.

Once you have done a few projects, they become easier. The first few projects I did were nightmares to supervise, and what the students turned in ended up not being very good. After 7 years of having students do multiple projects a year in mathematics, I now have high expectations for what the students will produce and how to help them achieve this level of work.

Here are some specific ideas you can use in your classroom for projects and the topic from mathematics they cover.

Functions and Logos – function transformations

Aunt Dot – arithmetic and geometric sequences

Threes and Ones – number patterns