There are different possible answers to this question, depending on the standard of proof one needs and the background knowledge one brings to the question.
Mathematical consistency and patterns
Try solving each of these problems, paying attention to the previous set of problems as you do so. Look for patterns to make solving the problems easier.
3 × 3 = ?
3 × 2 = ?
3 × 1 = ?
3 × 0 = ?
3 × -1 = ?
3 × -2 = ?
3 × -3 = ?
2 × -3 = ?
1 × -3 = ?
0 × -3 = ?
-1 × -3 = ?
-2 × -3 = ?
-3 × -3 = ?
The answers to these problems are below but I really do recommend taking the time to solve the problems above on your own first, so you get the sense of how students might think through this set of problems.
3 × 3 = 9
3 × 2 = 6
3 × 1 = 3
3 × 0 = 0
At this stage, many people will notice the answers are 3 smaller each time and the number being multiplied by 3 is one smaller each time, so they continue that pattern to answer the following questions.
3 × -1 = -3
3 × -2 = -6
3 × -3 = -9
Now, we decrease the first number in the pattern by 3 and one has to make some deductions about what the answer should be.
2 × -3 = -6
1 × -3 = -3
0 × -3 = 0
One might now notice that the answers are going up by 3 each time as we increase the first number, and so it is reasonable to continue this pattern.
-1 × -3 = 3
-2 × -3 = 6
-3 × -3 = 9
While to some this pattern may seem obvious, when someone is still in the middle of learning this concept, they have less cognitive capacity available to accomplish the task at hand (multiplying numbers together) and accomplish the additional task of looking for patterns in their answers, so this is where someone else prompting them to stop and look for patterns in their work so far will be very useful.
Prerequisite knowledge: One has to know what these symbols mean, what is meant by finding one number times another, and how negative numbers work in terms of counting down and subtraction.
Mathematical consistency and mathematical properties
Let’s look at a problem that we can do in more than one way, borrowed from the Khan Academy.
5 × (3 + -3) = ?
If we add the numbers inside the parenthesis first, then this is 5 times 0 which is 0, since 3 + -3 = 0.
5 × (3 + -3) = 0
But what if we distribute 5 through both terms first?
5 × 3 + 5 × -3 = ?
Since distributing the 5 across the addition does not change the value of the expression, we know this is still equal to 0.
5 × 3 + 5 × -3 = 0
But this means that 5 × 3 and 5 × -3 are opposite signs, so since 5 × 3 = 15, then 5 × -3 is -15. Let’s look at another example.
-5 × (3 + -3) = ?
We know that this is the same as -5 times 0, so this has a value of 0.
-5 × (3 + -3) = 0
Similar to before, we distribute -5 through both terms.
-5 × 3 + -5 × -3 = ?
Again, the distribution of terms does not change the value of the expression on the left-hand side of the equation, so the result is still 0.
-5 × 3 + -5 × -3 = 0
We know from before that -5 × 3 is -15 so we can substitute that value for -5 × 3 in the left-hand side of the equation.
-15 + -5 × -3 = 0
Therefore -15 and -5 × -3 are opposites since they add to 0, so -5 × -3 must be positive.
Nothing in what we did for the two examples above is specific to the value of 5 × 3, so we can repeat this argument for every other multiplication fact we want to derive, so these two ideas can be generalized.
Prerequisite knowledge: One has to know what these symbols mean, what is meant by finding one number times another, how the distributive property works, and how negative numbers can be defined as the opposites of positive numbers.
Representation on a number line
Imagine we represent multiplication as jumps on a number line.
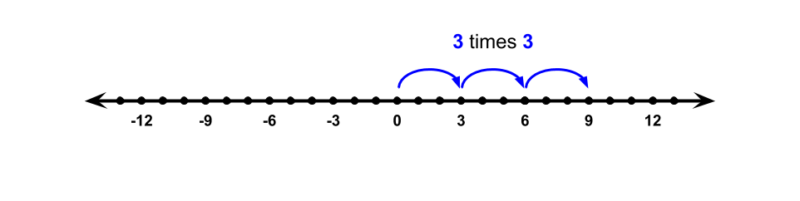
For 3 × 3, we draw 3 groups of 3 moving to the right. Both the number of groups and the direction of each group are to the right.
But what about 3 × -3? Now we have 3 groups of the number still, but the number is negative.
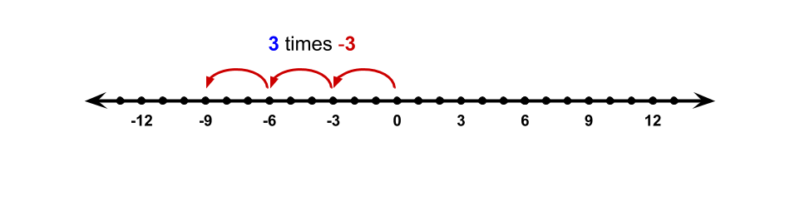
If we find -3 × 3, the size and direction of the number we multiply are the same, but now we are finding -3 groups of that number. One way to think of this is to think of taking 3 groups of the number away. Another is to think of -3 times a number as being a reflection of 3 times the same number.
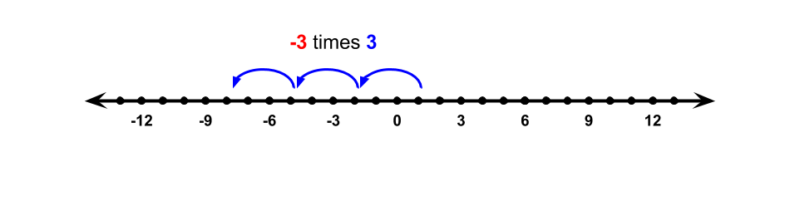
So -3 × -3 is, therefore, a reflection of 3 × -3 across the number line.
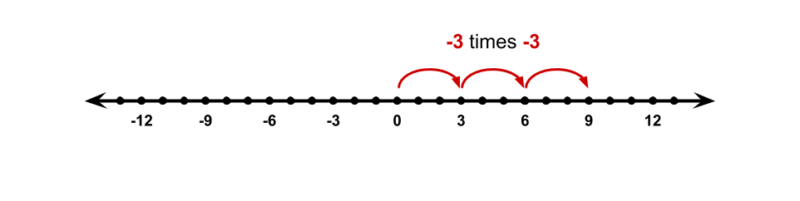
In one sense though, this visual argument is just mathematical consistency represented using a number line. If multiplication by a negative is a reflection across 0 on the number line, and we think of negative numbers as being reflections across 0 of the number line, then multiplication of a negative number times a negative number is a double-reflection.
Context
Karen Lew has this analogy.
Multiplying by a negative is repeated subtraction. When we multiply a negative number times a negative number, we are getting less negative.
This analogy between multiplication and addition and subtraction helps students nicely connect the two concepts.
Joseph Rourke shared this context.
A gambler loses $10 per day. How much more money did they have 5 days ago?
Here, the loss per day is one negative and going backwards in time is another.
@M_Teacher_w_T shared this analogy:
“An enemy of my enemy is my friend.”
This aims not at the algebraic or arithmetic properties of numbers but more at the oppositeness of negative numbers.
Prerequisite knowledge: All contexts that build new understanding require students to understand the pieces of the context fairly well, so it is especially important to probe how students understand an idea when it is presented contextually.
Algebraic proof from first principles
From Dr. Alex Eustis, we have this algebraic proof that a negative times a negative is a positive.
First, he states a set of axioms that apply to any ring with unity. A ring is basically a number system with two operations. Each operation is closed, which means that using these operations (such as addition and multiplication on the real numbers) leads to another number within the number system. Each operation also has an identity element or an element that does not change another element in the system when applied to it. For example, under addition, 0 is the additive identity. Under multiplication, 1 is the multiplicative identity. The full set of axioms required is below.
| Axiom 1: a + b = b + a | (Additive commutivity) |
| Axiom 2: (a + b) + c = a + (b + c) | (Additive associativity) |
| Axiom 3: 0 + a = a | (Additive identity) |
| Axiom 4: There exists −a satisfying a + (−a) = 0 | (Additive inverse) |
| Axiom 5: 1 × a = a × 1 = a | (Multiplicative identity) |
| Axiom 6: (a × b) × c = a × (b × c) | (Multiplicative associativity) |
| Axiom 7: a × (b + c) = a × b + a × c | (Left multiplicative distribution) |
| Axiom 8: (b + c) × a = b × a + c × a | (Right multiplication distribution) |
From these axioms, we can prove that a negative times a negative is a positive. I’ll reproduce Dr. Eustis’s proof below and include the reference to the axioms used. First, we prove that a = −(−a).
Corrolary 1| a = a + 0 | (Axiom 3 and Axiom 1) |
| a = a + (−a + −(−a)) | (Axiom 4 applied to −a ) |
| a = (a + (−a)) + (−(−a)) | (Axiom 2 – the associative property) |
| a = 0 + (−(−a)) | (Axiom 4) |
| a = −(−a) | (Axiom 3) |
So now we know that if we introduce negative numbers a is equal to −(−?).
Corrolary 2| 0 = a + (−a) | (Axiom 4) |
| 0 = (0 + 1) × a + (−a) | (Axiom 3 and Axiom 5) |
| 0 = 0 × a + 1 × a + (−a) | (Axiom 8) |
| 0 = 0 × a + (a + (−a)) | (Axiom 5 and Axiom 2) |
| 0 = 0 × a + 0 | (Axiom 4) |
| 0 = 0 × a | (Axiom 3 and Axiom 1) |
Proving that 0 = 0 × a is the kind of painfully obvious idea that hardly requires proof but it establishes a relationship between multiplication and the additive identity in the real numbers, which is not yet included in the axioms above.
Next, we prove that (−1) × a = −a.
Corrollary 3| −a = −a + 0 × a | (Corrolary 2 and Axiom 3) |
| −a = −a + (1 + (−1)) × a | (Axiom 4) |
| −a = −a + 1 × a + (−1) × a | (Axiom 8) |
| −a = (−a + a) + (−1) × a | (Axiom 5 and Axiom 2) |
| −a = 0 + (−1) × a | (Axiom 4) |
| −a = 0 + (−1) × a | (Axiom 3) |
Now, finally, we can prove that (−a) × (−b) = ab.
| (−a) × (−b) = (a × (−1)) × (−b) | (Corrolary 3) |
| (−a) × (−b) = a × ((−1) × (−b)) | (Axiom 6) |
| (−a) × (−b) = a × (−(−b)) | (Corrolary 3) |
| (−a) × (−b) = a × b | (Corrolary 1) |
This last “proof” though is unlikely to justify that a negative times a negative is a positive for any students though. It’s the kind of thing which is a required level of justification for a mathematician interested in rigorous proof who would likely consider the other justifications “patterning” and not sufficient.
A critical idea of proof though is that the intended audience of a proof is left convinced that an idea is true, and so I posit that the algebraic “proof” presented here is no proof at all for almost everyone.
Prerequisite knowledge: While I went through and added the justification for each step of the proof that was missing, I needed a fair bit of fluency with the original set of axioms. I also needed to not lose sight of the overall goal and to be able to recognize the structure of each part of the argument and match that structure to the axioms.
A simpler algebraic proof
This algebraic proof from Benjamin Dickman is much simpler than going back to a proof based on the axioms of arithmetic.
a + (−a) = 0
a × b + (−a) × b = 0 × b
ab + (−ab) = 0
From this, we can show that ab and –ab have opposite signs and therefore that a positive times a negative is a negative. Using the fact multiplication is commutative, a negative times a positive is also negative.
Similarly, we can prove that a negative times a negative is a positive.
a + (−a) = 0
a × (−b) + (−a) × (−b) = 0 × (−b)
−ab + (−a) × (−b) = 0
Since we know that −ab is negative, and the sum of these two terms is 0, therefore (−a) × (−b) is positive.
Prerequisite knowledge: The prerequisite knowledge for this proof is much less than the other one, but it does assume a fair bit of fluency with manipulation of algebraic structures.
Conclusion:
Given that the goal of an argument that something is true is to leave the other person convinced of the truth of the argument, whenever anyone uses any justification, representation, or proof, it behooves one to check that one’s audience is left convinced.
kentilton says:
Using the number line again, and considering just -1 as a multiplier and p as some positive number:
-1 times p produces -p, a value p units in the opposite direction on the negative range of the number line, and equidistant from zero;
if we multiply by -1 again, we get p, a value in the original position;
on the complex plane, multiplying by -1 is a 180 degree rotation;
I like to say, if I turn around twice I am going in the same direction.
Left as an exercise is generalizing from -1 to -n.
Next fun question: we tell students to reverse an inequality when multiplying both sides by a negative. Justify _that_!
March 15, 2020 — 5:19 pm
mike says:
If 0 < a a > b.
If a < 0 < b, flipping signs flips which sides of zero they're on, so b < 0 < a.
January 6, 2024 — 3:10 pm
Emma says:
I also like to show students that 9 x 9 (which they know is 81) is the same as (10-1)(10-1). Expanding to give the first 3 terms using the distributive law or the grid or box method yields 100 – 10 – 10 which gives 80. So -1 x -1 must be +1 to give 81 in total. Not a proof though!
March 25, 2020 — 3:14 pm
David Wees says:
That’s a really nice argument though that relies on consistency and student knowledge of the distributive property. “Hey look, we know these two things are true, therefore this third thing must also be true.”
March 25, 2020 — 3:47 pm
Craig Cyr says:
Awesome observation!!
November 20, 2023 — 6:45 pm
senan says:
That’s a great one to show it to primary kids while explaining negative times negative is positive.
December 28, 2023 — 10:44 am
Robert says:
Not a proof, but for an example in realia from the physical world of levers:
If you add weight (pos.) on the right side of the lever (pos.), the moment (pos. weight times pos. distance) is clockwise (pos.). –> + times + = +
If you remove weight (neg.) on the right side of the lever (pos.), the moment (neg. weight times pos. distance) is counterclockwise (neg.) –> – times + = –
If you add weight (pos.) on the left side of the lever (neg.), the moment (pos. weight times neg. distance) is counterclockwise (neg.). –> + times – = –
If you remove weight (neg.) on the left side of the lever (neg.), the moment (neg. weight times neg. distance) is clockwise (pos.) –> – times – = +
June 1, 2021 — 1:22 pm
Sugarbrenda@yahoo.com says:
That is absurd. If I owe my friend $1000 every month, I am in the negative by 1000 each month. -1000. If I have to pay for 10 months, -10×-1000 = -10,000. Now if by mental masterbation I can just say that two negatives multiplied equals a positive, then my friend owes me $10,000! Great, let’s tell my mortgage company!!!
October 7, 2023 — 3:07 am
David Wees says:
Paying for ten months is +10 × -1000 = -10,000 since the number of months you pay is a positive quantity. Using your analogy, what if your friend took away 10 months that you had to owe them 10,000? This is like -10 × -1000. How much money is this the equivalent of them giving you?
October 18, 2023 — 4:03 am
Warren Jones says:
so a couple years ago my son asked me why a negative times a negative is a positive, i didn’t have a good answer so we looked online for a proof, and i didn’t find anything i found super compelling, so i started trying to think about what we are literally saying
(-3)*5 is easier to understand because we are saying “5 groups of -3” or (-3)+(-3)+(-3)+(-3)+(-3), which tracks, but I think some of the cognitive dissonance is that subtraction is just adding the inverse. So what are we saying when we say 3*(-5)? 5 groups of the inverse of 3? if that is the case, then this also tracks ya? the inverse of 3 is -3 so 5 groups of (-3) which is (-15) ok so what are we saying when it’s (-3)*(-5)?
5 inverse groups of (-3)? which is 15.
does that sound right?
July 14, 2021 — 7:32 pm
Warren Jones says:
also thanks for this post, it would have been so helpful when we were initially looking, but maybe i wouldn’t have tried to reason it out like this if i had seen this.
July 14, 2021 — 7:33 pm
David Wees says:
Yeah, this is a good explanation, mostly because it makes sense to me and to you! That’s all that is really needed for an explanation to be useful — at least one person who understands it but of course two is ideal.
July 20, 2021 — 1:08 am
Krishna says:
But I am still surprised, what if a bag contains 5 rotten apples and we put 3 times of 5 rotten apples? Are they good apples 🍎? Contradictory of negative times negative is positive.
April 5, 2023 — 3:06 pm
David Wees says:
Putting is “a positive”, so putting 3 times of 5 rotten apples is adding 3 times -5 or +3 times -5. Instead, what if we had a bag of 15 rotten apples and we removed (eg. subtracted) 3 groups of rotten apples. Now the bag improves in quality by 15 rotten apples, eg. we added 15 good apples to cancel out each of the rotten apples in the bag.
April 6, 2023 — 9:41 pm
Denise says:
Oh wow. Lol. None of these explanations helped me. #WalksAwayInADaze
December 23, 2021 — 12:23 am
Eric says:
The real problem is trying to explain what a group of negatives is. People can visualize groups of things but a negative number of things has no physical meaning for them. Ultimately a negative sign just positions a number relative to zero. That is why in chemistry we have to use the absolute temperature scale for any mathematical calculations involving temperature. Zero degrees Celsius and zero degrees Fahrenheit are both arbitrary assignments.
April 19, 2022 — 11:52 am
Petr says:
Distances are more useful than “number of things” in this case.
September 4, 2022 — 12:39 pm
Hannah says:
I’m reading Neil de Grasse’ Tyson’s Origens. In it he states -3 *-3 = 9.
And this site agrees. I get it that a negative * a positive = 0.
For now I’ll just memorize a negative * a negative = a positive.
I’ll ask my school teacher daughter to explain it,
and thank you for trying to make it clear,
first time I used this good site! Hannah
October 13, 2022 — 12:33 am
David Wees says:
Yeah, sorry. I’ll see if I can find other explanations that may land for people. I focused on more algebraic ideas here but there are some visuals that might help.
November 3, 2022 — 4:15 pm
Ralph Cobo says:
Oh wow. You guys need to consider that numbers are directional vectors. The opposite of a vector is the negative (-) of that vector. Therefore -3 x -3 is the opposite of the direction sum -9 which is +9.
December 9, 2022 — 11:29 pm
lamarr says:
i use direction on a rail. you can only go one way, or another. a positive will tell you to proceed in the direction you’re going. A negative will tell you to turn around, no matter what direction you’re going. I don’t expect men to get this because who asks for directions? lol
December 12, 2022 — 6:15 pm
Denise says:
This one helps . Ha ha ha
March 2, 2024 — 9:37 am
BK says:
I really want to provide this response to my credit card debt! Spending $20 means my balance equals -20.00.
So, do that 3 times -3, and viola, -20×-3=60.
Hooray! They owe me!
Makes about as much sense as all the junk I had to memorize to get thru algebra and calculus. Mental masterbation.
July 29, 2023 — 9:26 pm
HD says:
Charging your credit card 3 times is a positive instance. So 3 x -20 = -60. It still checks out.
August 28, 2024 — 2:33 pm
james says:
I’m afraid Benjamin Dickman’s approach has one fundamental flaw.
It goes without showing that the distributive property can be used with a negative number composition at all.
When doing that it’s automatically assuming the legality of negative times negative…
August 7, 2023 — 9:52 am
howard says:
Another explanation about the number line diagram about negative times negative equal positive is that the point zero is the initial point,first negative,-a means you having decreasing values,times second negative,-b means you losing the amount by b times. -3 x -3 In this situation,you having the decreasing value,-3 when you at zero initial point,you losing it by 3 time,which you left the total decreasing values of -9,which means you gaining back your values,9.
October 8, 2023 — 12:36 pm
Zach Fairchild says:
This article showed proof of absolutely nothing. Every “proof” is assuming a negative x negative is a positive. It’s hard for people to comprehend, but you have to imagine a negative object existing. A negative apple sitting there, taking up space negatively. If I multiply 3 negative apples by 5 negative apples, they wouldn’t magically turn positive. They wouldn’t know what a positive apple looks like. What if I’m multiplying cells. Would all the negative cells I multiply together magically turn positive? No, and that’s why everything looks good on paper.
October 17, 2023 — 9:55 am
John Harding says:
Let (x-a)(x-a)=y
Then x^2 – 2xa + (-a)^2 = y
Now if y=0 then x=a
So a^2 – 2a^2 + (-a)^2 = 0
Then -a^2 + (-a)^2 = 0
Or (-a)^2 = +a^2
Ie. (-a) x (-a) = + (a x a)
So minus x minus = plus
December 6, 2023 — 8:58 am
Satish Shah says:
Superb proof.🙏🏽
January 30, 2024 — 8:13 am
Rajesh says:
How to write 2×0 & 0×2 both in a successive “addition” way separately in mathematics?
December 22, 2023 — 8:26 pm
mike says:
Apparently angle brackets destroy text.
To sum up : Flipping signs of all numbers (multiplying entire equality by a negative) swaps which side of zero a number is on while preserving relative magnitude, so the relation between them is inverted.
January 6, 2024 — 3:13 pm
Neena says:
How do you measure the magnitude of a literal number?
July 29, 2024 — 7:49 am
Dustin Robert Kengott says:
How does this debate differ from people who claim that 0.9(repeating) is equal to one?
…
A nine-fold absence of something that is thrice absent already is not a miracle made.
Like this: I overdrafted $100.00 from my bank account so now I am only eating food that I can buy 2-for-1 until my debt is washed.
I owe you a dollar? No problem, here is a cheeseburger.
Wait just a second, the sale paper says pickles are buy one get one free, and if you can’t find anywhere that cheeseburger is accepted, I will consider taking it off your hands for $0.50.
Yah I bet 27-more of anything is looking pretty good now that you sat on someone’s discarded chewing gum…
Oh man, I love seagulls.
January 22, 2024 — 6:33 am
Eritheus says:
Hello, why does the -3 x 3 example move from 1 to -8 on the graph?
April 6, 2024 — 2:17 am
Scott says:
Easy peasy, 2 negatives are positive. This is Truth. Galatians 3:13-“Christ hath redeemed us from the curse of the law, being made a curse for us: for it is written, Cursed is every one that hangeth on a tree:” The curse is negative, Christ was cursed, the result is POSITIVE! That settles it for me! glory to God!
September 7, 2024 — 2:44 pm