I’ve been thinking a lot recently about what knowledge is needed by mathematics teachers in order to be excellent teachers. It is clear to me that teachers of mathematics must know the mathematics they are to teach, but what else do they need to know?
(Source: Content Knowledge for Teaching: What Makes it Special?)
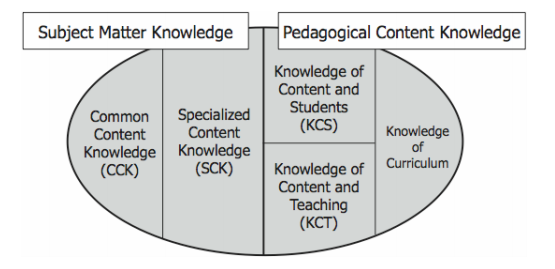
I’m not the first person to wonder this. In a 2008 paper, Deborah Ball, Mark Thames, and Geoffrey Phelps describe a categorization of the mathematical knowledge needed for teaching into five broad types, described in more detail below.
Knowledge of mathematics
- Common mathematical knowledge:
Deborah Ball et al. describes this as “knowledge that we would expect a well-educated adult to know” (Ball, Content Knowledge for Teaching. What makes it special?, 2008). It is closely associated with the curriculum that is being taught and includes knowledge of when students are making mistakes and when there are errors in a textbook.
For example, common mathematical knowledge includes knowing how to subtract a negative number from a positive number. It includes knowing how to multiply multi-digit numbers together. It includes knowing how to solve a quadratic equation by factoring. It includes all of the mathematical knowledge necessary to solve mathematical problems in at least one way.
Note that teachers should at least know all of the common mathematical knowledge they are expected to teach as well as how that knowledge is connected to the mathematics students are likely to learn later in school. If I teach my students that an equals sign (=) means “find the answer” they are likely to find algebra confusing until they learn that the equals sign means “the two expressions on either side of this = sign are equal in size”.
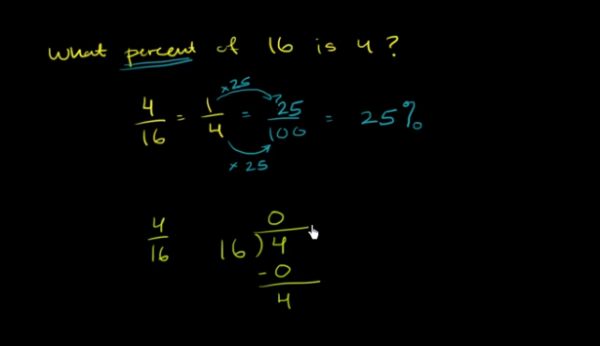
(Source: Finding a percentage)Notice in the example above, the author of this video is dividing 4 by 16. Instead of making sense of the calculation, he starts by following the algorithm which results in a non-sensical calculation. Someone who understood this division calculation with a stronger conceptional understanding might realize that since 16 is larger than 4, we can skip the first iteration of this division calculation and move straight away into 40 divided by 16.
When teachers lack this mathematical knowledge, they often end up relying on tricks instead of mathematical understandings. In my own practice, I remember when I was first called upon to teach the Chi-squared test, which at the time I did not know. I read ahead in my textbook and figured out how to follow the mathematical recipe that produced the Chi-squared calculation well enough to muddle through it in class. However years later I finally connected the expected values to probability and realized that I had for many years missed an opportunity to help students make a connection between this test and other things we were learning that year.
- Specialized mathematical knowledge:This is “knowledge beyond that expected of any well-educated adult but not yet requiring knowledge of students or knowledge of teaching” (Ball, 2008). For example, knowing some of the many different representations of positive and negative numbers is mathematical knowledge that one could not expect every well-educated adult to know, and does not require knowing students or teaching.
An example of specialized mathematical knowledge is knowing how to represent subtracting a negative number from a positive one in a variety of different ways. Since different students are likely to find different models for understanding current topics more or less easy to grasp, it is incredibly useful to know a variety of different ways of representing and approaching each area of mathematics that is taught.

Different models for understanding subtracting negative numbers
Knowledge of students:
- Pedagogical content knowledge
- Knowledge of the ways students understand the content:This is the knowledge of not just the ways to do mathematics but the ways in which students understand the mathematics. While some mistakes students make are the result of over-taxed memory or carelessness, not all mistakes students make can be explained in these ways.

(Source: Math Mistakes)What mistake did this student make above? What does this mistake mean they were thinking when this did this calculation? How would you help this student? Answering all three of these questions requires an understanding of the ways student understand this mathematical content.
Magdalene Lampert once told me the story of an interaction she had with a 5th grader. Near the very end of a class discussion, he said that 0.007 is negative. The class ended and Magdalene was left to try and figure out why the student thought that 0.007 is negative. If teachers have the common mathematical content knowledge they need, they should understand that 0.007 is not negative. If teachers have sufficient knowledge of the many different ways students might understand mathematics, then they will know that there is a fairly logical (although incorrect) train of thought that leads students to the mistaken understanding that 0.007 is negative. Any guesses as to what this student was thinking?
- Knowledge of the ways to teach mathematics:This is the knowledge of how to teach mathematics so that it makes sense to someone else. It includes thinking about the sequencing of mathematics concepts as well as knowing rationals for why various pieces of mathematics are correct. Teachers need to make choices about what mathematical representations to use with students and which of those representations are likely to understood and misunderstood by students.
In my previous example, knowing the different models of understanding the mathematics is specialized mathematical knowledge, knowing which models to choose and how to sequence the models is mathematical knowledge for teaching.
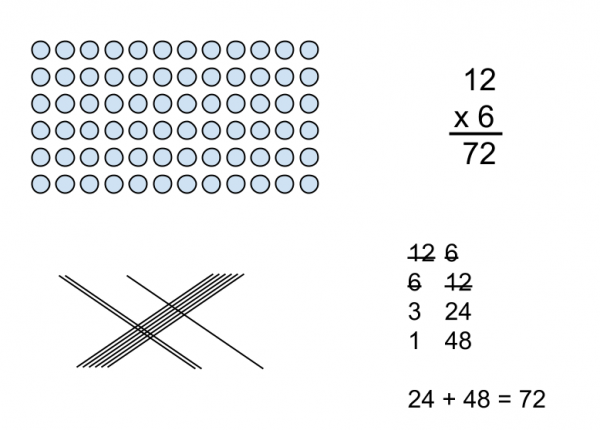
Different ways of representing 12 times 6These are a few of the different models for understanding multiplication. Which of these models do you think work best for initially introducing multiplication? Which of these models is most efficient? How are these models connected to each other?

(Source: Jason Zimba, NCTM 2014)When teachers do not know how to teach a particular idea to students in ways that make sense to students, they may rely on mnemonics or other non-mathematical ways for students to remember mathematical content. If you look at the example above, it is clear that whoever created these diagrams is hoping that these will help students remember the math facts for 3×3 and 3×4. Wouldn’t it be better though for students to understand at least these simple multiplication facts based on pictures of what they represent or at least be memorizing the words that represent this relationship?
This area of knowledge also includes how to ask questions in class that get all students thinking, how to give students feedback that helps them move forward, and how to choose instructional activities that support students learning mathematics.
- Knowledge of the curriculum:Teachers also need to know the scope and range of the mathematics they are teaching. They need to know the standards that are appropriate for their particular course as well as what those standards mean. They need to know what resources they have available as well as how useful those resources are for their teaching. They need access to curricular resources and because of the limited time teachers typically have available to plan, they need to know where to find the resources they need without spending an enormous amount of time searching.
- Knowledge of the ways students understand the content:This is the knowledge of not just the ways to do mathematics but the ways in which students understand the mathematics. While some mistakes students make are the result of over-taxed memory or carelessness, not all mistakes students make can be explained in these ways.
There is other knowledge teachers need to know outside of the knowledge related to their content area.
Knowledge of students and schools
- Knowledge of students’ cultures and backgrounds:While this is not typically included in the lists of knowledge required for teaching, it is pretty clear to me that it is necessary. The ignorance that led this group of NYC teachers to not only wear these t-shirts but to also pose for a photo is a clear sign that there is a body of knowledge about students’ culture and teachers’ impact on it that exists and that not all teachers know.
- Knowledge of the emotional needs of students:Teachers are also responsible for understanding the emotional needs of the children under their care. These needs change over time and are different for different children. Teachers need to pay attention to the status needs of their students and to understand how status impacts their classroom instruction.
Who can be grouped with whom? Who looks like they need more support today? Which children look like they are being abused or neglected? Who is likely to be excited by today’s lesson?
- Knowledge of the rules and procedures related to teaching:Every school has procedures teachers are expected to follow and every country and state has laws teachers are expected to obey. While knowledge of these rules and procedures is completely insufficient to be able to teach, a lack of knowledge of these rules and procedures has led many educators to disaster.
Conclusion:
From my own experience, I learned very little of this before I started teaching, aside from the knowledge of most of the mathematics I was employed to teach. During the course of my career as I attempted to make sense of what students understood and planned lessons to build student mathematical knowledge, I slowly built up my understanding of these areas of knowledge.
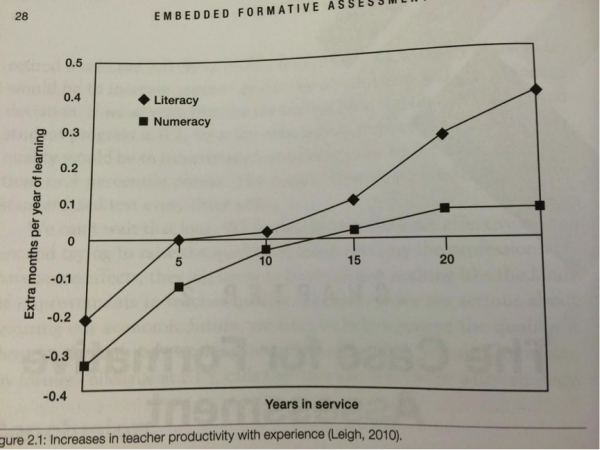
(Source: Embedded Formative Assessment)
The graph above shows a summary of research on the correlation between how many years of service literacy and numeracy teachers have compared to how much their students learn. Early in their careers, both teachers of literacy and numeracy struggle to use the knowledge they have to successfully teach students. One way of interpreting the graph above is that as they progress through their careers, both teachers of literacy and numeracy increase their knowledge of how to teach, and their students benefit.
What of the knowledge above can teachers begin to learn before they start teaching? How can we ensure that every teacher of mathematics learns enough of this content during the course of their career in order to be able to teach? Also, how does this post relate to teachers of other content areas or elementary school teachers?
References:
Ball, D. L., Thames, M. H., & Phelps, G. (2008). Content knowledge for teaching what makes it special?. Journal of teacher education, 59(5), 389-407.
Wiliam, D. (2011). Embedded formative assessment.
Howard Phillips says:
Hi !
I followed the link to Embedded Formative Assessment and read the first 10 or so pages that Amazon allowed (not entirely consecutive). WOW! Even allowing for the author’s desire to quote favorable research the story is quite amazing. I almost feel like sending a copy in the mail to Bill Gates.
Regarding your examples, I thought that 12+12+12+12+12+12 was the natural way to describe multiplication, with nubers or with bricks. And the kid who did 34×68=98 hasn’t got a clue about the sizes of numbers.
Regarding the term Formative Assessment, I think that using the word “assessment” gives the wrong impression. It suggests that the activity is being carried out in order to generate records of achievement.
September 29, 2014 — 6:17 am
Raymond Johnson says:
Ball, Thames, & Phelps (2008) seems to be a popular article to blog about — I’ve written one and so has Bud Talbot, and I’ve added a link to this at the bottom of http://mathed.net/wiki/Ball,_Thames,_%26_Phelps_(2008).
I caught one very interesting thing as I was reading this: you say specialized mathematics/content knowledge is “knowledge beyond that expected of any well-educated adult but not yet requiring knowledge of students or knowledge of teaching,” and that didn’t sound right to me. It appears that in the preprint you link to and cite, that is indeed how Ball et al. define SCK, but in the published version in JTE it is defined as “the mathematical knowledge and skill unique to teaching” and that “SCK is mathematical knowledge not typically needed for purposes other than teaching” (p. 400). I’m sure Ball et al. had some interesting discussions that led them to change this definition in the final version!
September 30, 2014 — 9:56 pm
David Wees says:
I can think of one reason for this change in definition; if we are trying to define knowledge needed for teaching, then under the definition used in the version I cited, there could be specialized mathematical knowledge that teachers have that is above and beyond what we would expect from a well educated adult, but that does not in any way assist them in their teaching.
October 1, 2014 — 5:25 am
Howard Phillips says:
I found this bit in the Embedded book. Seems relevant.
“Some progress has been made in determining what kinds of teacher knowledge do contribute to student progress. For example, scores achieved hy elementary school teachers on a test of mathematical knowledge for teaching (MKT) developed by Deborah Ball and her colleagues at the University of Michigan did correlate significantly with their students’ progress in mathematics [Hill, Rowan, & Ball, 2005). Although the effect was greater than the impact of soccoeconomic status or race, it was in real terms small; a one standard deviation increase in a teacher’s mathematical knowledge for teaching was associated with a 4 percent increase in a student’s rate of learning. In other words, students taught by a teacher with good MKT (that is, one standard deviation above the mean) would learn in fifty weeks what a student taught by an average teacher would learn in fifty-two weeks—a difference, but not a big one. Or, to put it another way, we saw earlier that one standard deviation of teacher quality increases the rate of student learning by around 50 percent, and we have just seen that one standard deviation of pedagogical content knowledge increases the rate of student learning by 4 percent. This suggests that subject knowledge accounts for less than 10 percent of the variability in teacher quality.”
October 2, 2014 — 5:29 pm
David Wees says:
Mathematical knowledge for teaching is just one component of the mathematical knowledge teachers need. See my post above for the others. The last sentence is in error if everything else from Embedded Formative Assessment is totally true. It should read “This suggests that mathematical knowledge for teaching accounts for less than 10 percent of the variability of a proxy for teacher quality; how much their students learn.”
October 3, 2014 — 8:17 am
Howard Phillips says:
I guess they didn’t proof read properly.
In any case, when people have an axe to grind they can be very selective in their choice of research references. I do however wonder how they measured “teacher quality”. And on re-reading the quote I wonder too how they measured MKT, and if most of the teachers had the basic knowledge then they were measuring the excess. One might reasonably conclude then that this extra wasn’t going to make so much difference. This sort of statistical inference is quite useless unless one knows a lot more about the actual data and the methods of data collection.
October 3, 2014 — 11:31 am
Zaza Jack says:
This article was fruitful for my writing. It made my writing meaningful.
November 21, 2017 — 5:36 pm
Philani says:
Please help me . I have an teaching online module. I’m busy with a portfolio. I’m required to write about teachers specialized knowledge. What should I write
October 23, 2019 — 3:09 pm
David Wees says:
I’m not sure. One idea might be to pick a mathematical topic and explore typical errors students might make and describe strategies for supporting these different ways of thinking, then connect all of this to how this is a kind of specialized knowledge that only experienced teachers have — considering and diagnosing student thinking.
October 23, 2019 — 3:22 pm