Tag: The Reflective Educator (page 1 of 43)

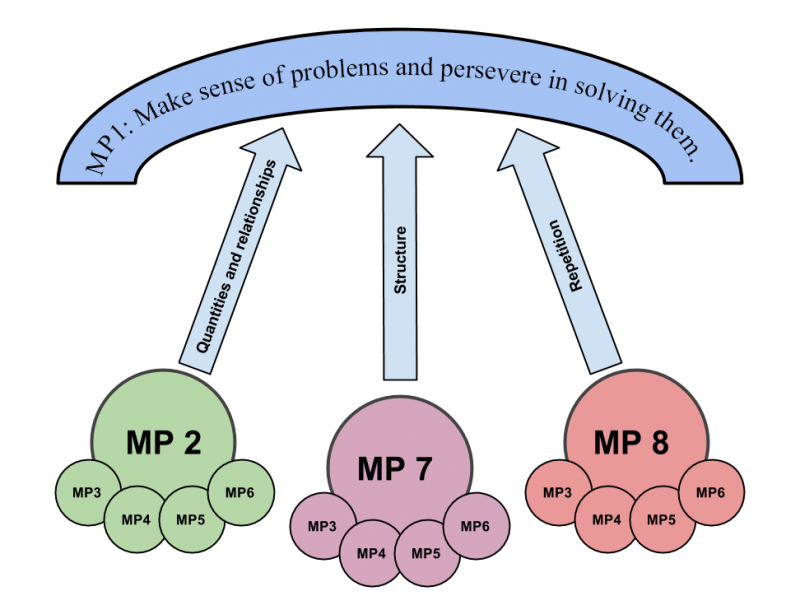
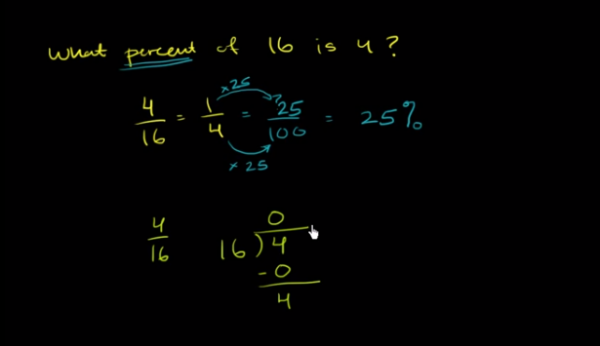Here are my slides and my notes from my five minute Pecha Kucha-style presentation at Educon. The focus of my presentation was on my journey as someone who started his teaching as viewing students as mistake makers to being a teacher who views students as sense-makers.

1. I’m going to talk today about my journey from a teacher who tried to correct students’ mistakes to someone who paid attention to student thinking and participated in mathematical reasoning with my students.

2. When I first started teaching, I monitored students’ behaviour, carefully recording dots when they failed to hand in their homework, dots when they were late, dots when they did not participate, dots when they were absent. I held those dots over my students’ heads like the Sword of Damocles. I was the dot master!

3. I noticed that my students made predictable mistakes and I modified my lessons to address those mistakes. “Don’t forget to change the sign of the second number.” “x times x is x-squared, not 2x.” “Don’t cancel the x’s!”

4. However, I was often confused by what they were doing. I became curious about where student mistakes come from. Why is this student writing a +1 there? What does this mean to him? Why are students doing these crazy things??

5. I began to realize that what students said and what they did was the result of something they were doing that I could not directly observe. I formed a hypothesis: students think. In fact, I realized that students think quite a lot.

6. I thought my job was to intervene on how they were thinking rather the product of that thinking. I realized that if what students do is a product of their thinking then I need to know what they are thinking not just what they write. I needed to be able to read minds.

7. Unfortunately, I still thought my job was to fix their thinking as if it were something that had been broken by their experiences. I thought that my students were just thinking wrong things, and therefore all I had to do was correct their thinking.

8. “A teacher is a mechanic for the mind”, I said to myself, “And in order to repair it, I just need to know how it works.” I wanted to reach into my students’ minds and fix them. I viewed my students as broken and my job was to make them whole again.

9. I listened to what my students said. I carefully watched what my students did to help me prognosticate their actions. “If I just know enough about how they think,” I thought, “I can help them think better.”

10. I was judge, I was jury, and I executed based on my understanding of student thinking. I tried students for the crime of thinking differently than I and sentenced them to more explanations of the only truth that mattered, my truth.

11. This approach has flaws. It has limitations. 10 thoughts per kid. 20 kids a class. Six classes a day. Five days in a week. 34 school weeks in a year. That’s 204 thousand thoughts a year to pay attention to. It was overwhelming.

    
    

12. And you know what? One day I realized that the way the kids thought yesterday wasn’t the same they thought today. What I learned about student thinking was out of date by the time I wanted to use it because, just like me, kids don’t think the same way everyday.

13. I needed to be able to responded to thinking live in the moment, rather than teaching while blindfolded. I started having mathematical conversations in the moment with my students and listening to them have conversations in order to uncover their thinking and respond now.

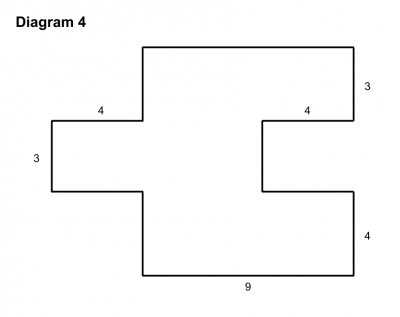
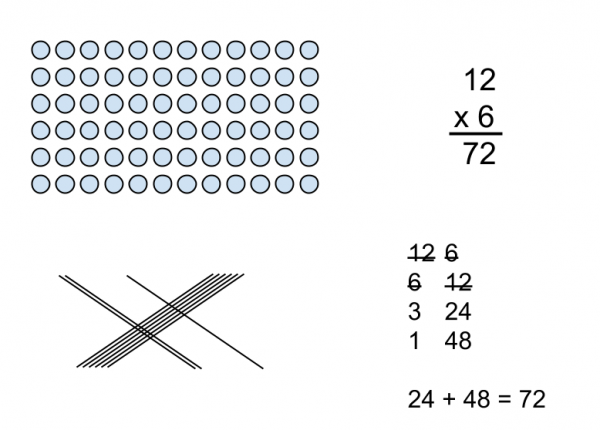
14. I anticipated student thinking instead of student mistakes. Here’s 11 different ways I solved a problem. Guess how many of these ways were actually used by my students? None of them. Human cognition is incredibly complex.

15. I questioned my beliefs about mathematics and why we teach it. What do I want my students to get out of mathematics class? More importantly, what do my students want to get out of mathematics class?

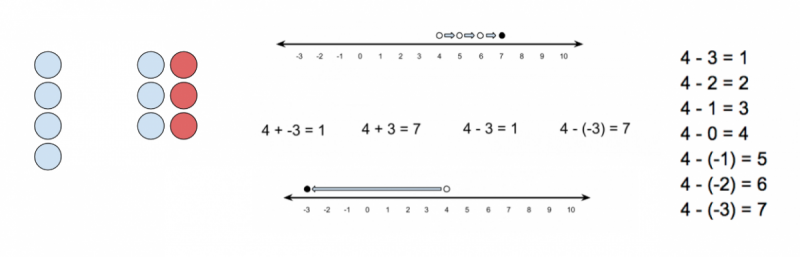
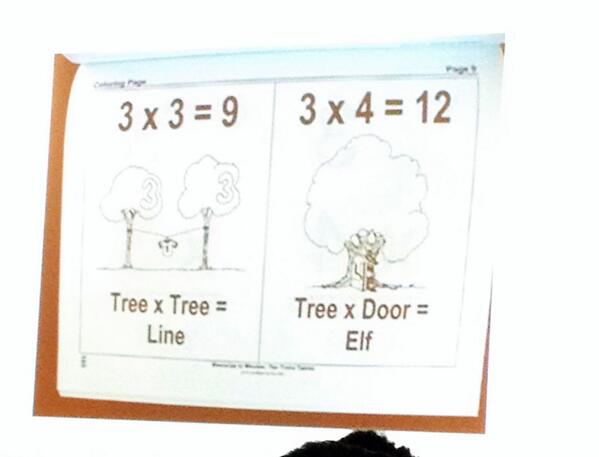
16. We are conditioned to think of ideas like this as being right or wrong, correct or incorrect, true or false. Instead, let’s figure out how what this kid has done make sense to her. Let’s remember that that students’ mistakes are the result of thinking.

17. There are other benefits to making student thinking visible in a classroom. An ongoing mathematically-rich conversation engages all of my students in thinking about mathematics in ways which give them agency and authority.

18. How do we design mathematics classes where students don’t end up thinking they’ve spent 13 years memorizing arcane rituals? Let’s make mathematics class about learning about thinking rather than about trying to avoid mistakes.

19. Children are not broken! It is not our job to treat them as things to fix. Children are sense-makers! Our job as educators is to provide experiences so students develop models for understanding the world.

20. Here are my sons. Let’s work together to build a world that treats them and all other children as sense-makers within it.

Here, go and read through this task from Illustrative Mathematics. I’ll wait for you. Pay attention to the use of academic language in the task.

Here are the academic vocabulary words I noticed students would need to understand (in an academic sense) in order to be able to do this task without any support:

table, random, data, scatterplot, selected, relationship, linear, equation, least squares regression, line, interpret, points, variability, estimate, expect, more than, less than, predicted, amount, more, less, residual, difference, calculated, plotted, corresponding, number, set, explain, determine, appropriate, describe, sample, diameter, plot, fit, area

Students might not know some of these words and still be successful task as they can use the other words (including the non-academic vocabulary) in order to make sense of what those words mean. It could also be that through doing this task and talking with other students about it, they can learn some of the words that they did not know.

All of these words are important words for students to know and to be able to use in appropriate contexts if students are going to be able to participate in the wider mathematics community. We cannot strip language, either common or academic, from our mathematics classes and expect students to be successful. As Harold Asturias has reminded me a few times, in order to have complex ideas, we need complex language to describe those ideas.

On the other hand, we can be thoughtful and deliberate in how we introduce new words to describe ideas to students. Specifically we can:

• When students describe an idea but do not use the language a mathematician might to describe it, you can revoice their idea (or other students can) using the language that a mathematician might use, being careful not to introduce so many new words that students cannot piece together what each of them means.
• You can use mathematical problems with sufficient text for students to make sense of the mathematics and to use the context to make sense of the new words to which they are being introduced. Again, words should be introduced strategically because a page full of words students don’t know will sound like gibberish to them.
• You can introduce words through multiple contexts including text, words, visualizations, mathematical problems. This way students can make sense of what the word sounds like, would be used in a sentence, would look like if drawn, and how it applies to mathematical ideas.
• You can use the mathematical practices to situate the language students need to learn within the context of the problems they are trying to solve.

What else can we do to help students use language to make sense of mathematical ideas?

As part of homeschooling my son, I recently started teaching a mathematics class to a group of 8 to 10 year olds on Saturday. In this class, I decided to use the TERC investigations curriculum. After reading through the curriculum overview, I decided that the major focus of the first unit of each year is about helping students preview the mathematics to be learned for the year and investigating as a teacher what students currently understand. 

The very first investigation for grade 3 is on counting out 100 snap blocks. In this task, students are prompted to explain how they are sure they have 100 snap blocks. The goals of the task are to investigate how students understand numbers represented in a visual way and to learn how they communicate mathematical ideas to each other orally as well as in writing.

Before I decided to use the task with students, I decided to try a few different strategies myself to try and anticipate what strategies students might use. Here are a few of them below.

As it turned out, only one of these strategies was actually used by students in the class. I uncovered this, while students were working on this task, by circulating between groups and looking to see what students were actually doing.

One group started with a 5 by 5 square they had already built during the free exploration time, and built out into a 10 by 10 square. As it turns out, I built my 10 by 10 square by snapping together 10 columns of 10 blocks so even this very similar strategy did not exactly match my thinking. This group finished quite quickly and when asked to find another way of proving they had 100 blocks, did not do so. Instead they worked on improving their explanation.

Another group decided to split the task of counting in half, and realized this meant that each of them would be responsible for counting out 50 blocks. However, when they started working, they did not communicate with each other very well on their plan for counting and for the first several minutes they just put blocks together. Upon observing this, I asked them what their plan was, which required them first to communicate about a plan. One of the students decided that 50 blocks could be counted as two rows of 25 blocks, and that 25 blocks could be represented as a 5 by 5 square, and so they each individually created a 5 by 5 by 2 block, and put it together on the height 2 side, forming a 5 by 10 by 2 block.

The final group just started by snapping blocks together as quickly as they could without keeping track of how many blocks they had, but they did attempt at least to keep their blocks in a rectangular prism form. I asked them what their strategy was, and one of them indicated that they were not counting because they planned on counting later once they were pretty sure they had 100 blocks. I then decided to keep asking them how many blocks they had every time I checked in with them. Finally I asked them to stop building and just count how many blocks they had.

At this stage the students had a 5 by 5 by 4 rectangular prism. As the students counted their blocks, I noticed that they had to count the lengths of each side each time, and had to count the number of blocks on each face each time, and did not seem to be subitizing this collection of objects. I also noticed that their strategy for counting all of the blocks was to count the surface area of four sides of the whole block ending up with 20 + 20 + 25 + 25 for 90 blocks total. I wondered why they had chosen only four sides with this strategy instead of a more consistent six sides, so I asked them how many sides the block had. They counted it out by rotating the shape, found the block had six sides, and decided that in fact they must have 20 + 20 + 20 + 20 + 25 + 25 blocks.

At this point, I thought about ending the counting activity and having groups come together, but I decided that because the students did not know each other very well, and because I had not done very much work on constructing community norms around how work is shared, it would not be very productive for this group to come and present their model at this time. Instead, I pointed at one of the corner blocks asked the students how many times this one block was counted with their scheme, and one of the students quickly noticed that it would be counted three times, at which point one of the other students said, “Oh” and decided to count the blocks by “counting the groups of blocks”. He basically counted out one row of 5 by 4 to find out how many blocks were in one row and then counted out the 5 rows of blocks to come up with 20 + 20 + 20 + 20 + 20 = 100 blocks. The first student looked clearly convinced that this meant they had 100 blocks so I decided to continue to be uncertain as to whether the third student in this group was convinced and end the activity.

As the students got together, I decided to sequence their explanations from the group that counted out half of the blocks, the group that counted out the big rectangular prism, and end with the group that counted out a 10 by 10 square. Each group shared their strategies while I prompted them to explain their work more completely.

After the class was over, I took time to write notes to myself on what I noticed during the class, to help me plan the class for the following week. I looked at what the students wrote down as their explanations on paper, and decided that these did not capture enough of the thinking students did to be very useful to me, except that I became acutely aware that all of my students need work constructing coherent explanations.

My goal for this group of students is to develop their capacity to use arguments and evidence to justify the mathematical ideas they uncover with each other to form a community of mathematicians. I want them to be curious about how each other understands the mathematics and to use their shared understanding to extend and build on their individual understanding of the mathematics.

The formative assessment process I used during this lesson could be summarized with the following steps:

1. Do the mathematics myself and anticipate how students might do the task,
2. Give the task to students to do,
3. Observe what students actually do and what they say to each other while they work and ask questions to clarify my understanding of the strategy they are using,
4. Intervene in the student thinking only when necessary and only when a useful intervention seems clear to me.
5. Use my growing knowledge of how the students understand the mathematics as a basis for my decisions, both in-the-moment and to inform future work with these students.

The process I’ve described above does not require an exit ticket, it does not require different coloured cups on tables, it does not require daily quizzes. It requires me to plan what thinking I hope and expect to see and to build a model of how students understand the mathematics and to carefully select how I will support students in developing their understanding.

Formative assessment is more of a mindset on using student thinking as the basis for teaching and learning rather than a quick checklist or a list of strategies.

I have just three words of advice. Study your teaching.

You can’t control where your students come from, and you can’t control what their parents do, and you can’t control how society views them, and while all of these things are important, you can only pick a part of the problems you see and start working. Every dirty floor that gets cleaned starts with a single sweep of the broom.

Study your teaching.

What do you do that makes an impact? What do you have control over? Where can you make a difference? What are your goals for this group of students you have on this day in this place. Why are these students struggling and yet these ones are not? How do I move my students from here to there, and where is here anyway?

Study your teaching.

It’s up to no one else. You are in control of whether you improve or stay the same. Whether or not you preach personal responsibility for your students, you need to accept it for yourself. Take charge of your learning and make the assumption that you can always get better.

Study your teaching.

You know that no matter what anyone says, teaching is hard work. It just might be the most difficult work ever conceived. Fermat’s Last Theorem was once thought of as one of the most challenging problems in mathematics, but at least it is solved. We still don’t know how to ensure that every kid has the same opportunity to reach their full potential or even if this is a useful way to frame the challenges of teaching. Teaching is the noble profession that enables everyone’s dreams.

Study your teaching.

If you believe that teaching is hard, then why are you trying to do it alone? There is an old African proverb that says if you want to go quickly, go alone, but if you want to go far, go together. The journey to excellent teaching is long and hard and you will need to work with other people to reach it.

Study your teaching.

Educational fads come and go, but you should be curious why this is so? Why is it policy makers are always trying something new? Study for yourself what works and what does not. You must work with your colleagues to incrementally improve what you do, because in a world focused on quick fixes, no one else will.

Study your teaching.

It makes the work continually interesting. Instead of just marching through what you have always done, be curious about what you do and try out new things. The unexamined life is not worth living, but it is more appropriate to say that if you aren’t curious in what you do, you aren’t living at all. Life is too short to treat teaching as just a job. One source of happiness is curiosity.

Study your teaching.

Be systematic. Make no assumptions about what works and what does not. If everyone really understood the ideal path through which people learn, there would be no one like me still studying it. Be careful to examine your own biases and models for understanding the world. What led you to believe in x, and how do you know x is true? And if other people do not believe in x, why not? What is different about what they know and what you know?

Study your teaching.

What does it mean to teach? What are we trying to teach? Do you teach mathematics or do you teach children? Can you be human without attending to other people’s emotions? They say that they will never remember what you say, they will only remember how you made them feel. Is this true, and if so, how are you making your students feel?

I have only three words of advice, but if you heed them, then you have your life’s work ahead of you.

Study your teaching.

In 2014, I only wrote 50 blog posts (3 are still unpublished) as compared to 2013 when I wrote about 180 posts. I wrote a lot less this past year in the previous year, at least on this blog. Is this a sign that I have less to write about? Or is this a sign that I just have less time to write? I tend toward the latter explanation, given how much work it is to keep up with my two-year-old son…

I wrote about a lot of different topics, including formative assessment, social media, language and learning, strategic inquiry, using mathematics, and ways students can understand mathematics. I found myself writing and tweeting quite a bit less about technology and tools this year and quite a bit more about processes.

My most popular posts, as measured by page views, were on effective mathematics teaching, using mathematics to choose my next apartment, 20 things I think every teacher should do, categorizing student work, ineffective feedback and the Khan Academy, the confirmation bias cycle, and what mathematics teachers need to know.

The posts that took me the most time to write were on effective mathematics teaching, ineffective feedback and the Khan Academy, supporting english language learners in math, sharing individualized comments using Autocrat, and what mathematics teachers need to know. From a time-to-write to number-of-views ratio, my post on the confirmation bias cycle is a huge hit. My favourite post from the year is on what mathematics teachers need to know.

My blog has been viewed over 9 million times since I started blogging and has generated 1889 comments. This year’s posts have amassed 275 thousand views and generated 95 comments, both of which make sense given that I have far fewer posts than usual and that most of my page views each year come from older posts.

I’m looking forward to the new year. I have some projects that I have been working on that will be fun to blog about. I’m particularly interested in learning more about how teachers develop as teachers and what potential learning trajectories look like for teacher knowledge.

The Problem

Imagine you have a list of possible questions you want students to be able to understand and be able to translate into mathematical symbols, like the following.

1. The sum of six and a number
2. Eight more than a number
3. A number plus five
4. A number increased by seven
5. Seven more than a number
6. The difference of five and a number
7. Four less than a number
8. Seven minus a number
9. A number decreased by nine
10. The product of nine and a number

One common approach I have seen used is to model a few of the questions on the list and then ask students to attempt the other problems themselves or in small groups. This approach has a serious flaw; it requires students to know the thing you are trying to teach in order to do the task.

Let’s imagine a very similar task, except now suppose I ask you to translate the list into German. Here are the first two phrases translated into German (thank you anonymous translators).

1. Die Summe von sechs und eine Zahl.
2. Acht mehr als eine Zahl.

Now translate the other 8 sentences.

Unless you already know German, you can’t do this task. Worse, imagine I gave you the entire list in German and asked you to translate it into Hebrew.

1. Die Summe von sechs und eine Zahl.
2. Acht mehr als eine Zahl.
3. Eine Zahl plus fuenf.
4. Eine Zahl von sieben vermehrt.
5. Sieben mehr als eine Zahl.
6. Der Unterschied von fuenf und einer Zahl.
7. Vier weniger als eine Zahl.
8. Sieben minus eine Zahl.
9. Eine Zahl verringert bei neun.
10. Das Produkt von neun und eine Zahl.

Here are the first two phrases translated into Hebrew. Translate the rest of the phrases from German.

1. החיבור של שש ומספר
2. שמונה יותר ממספר

Unless you know German well enough to understand the phrases in the first place and Hebrew will enough to translate the German, you cannot do this task. You also cannot do this task if you do not know how these phrases are related to each other in the two different languages.

If your students do not know the vocabulary in the first list I shared and/or they do not know the mathematical symbols, then they cannot do the translation between the two without some intervention.

A solution:

However, students may be able to use their partial knowledge of the symbols or the vocabulary to fill in gaps in either. As an alternative to having them work on the entire list from scratch you could:

• Give them a copy of both lists and ask them to individually match as many of the items as possible and then attempt to match the other ones as best as they can. They could then work in groups to refine and improve their lists and then individually try to write out the situations using actual numbers.
• Embed the different phrases in a context through which students could make sense of the relationships between the symbols and the text. One issue here with making sense of what these phrases mean is that students do not have sufficient clues as to what they could mean because the phrases are completely contextless. There is not enough information provided as to what these phrases actually mean. Here’s an example of a task based on equality instead of inequalities but hopefully you can generalize what I mean from it.

If students have insufficient knowledge of either the vocabulary or the mathematical symbols, then they need to build that knowledge first. In this case, these ten recommendations on building vocabulary may be useful to consider.

Additional point:

The original goal is probably not a very good goal given that students are rarely, if ever, asked to translate phrases this short into mathematical terminology. Instead of focusing on the small building blocks students might use to translate phrases, it is more useful to start with longer phrases based on meaningful contexts (note: this does not necessarily mean real world) that include more text and to work with students to reduce these phrases to simplest form, and then use these reduced forms to look for mathematical connections between the longer forms of text.

(Source: Engaging ALL students in Cognitively Demanding Mathematical Work, November 4th, 2014)

On Tuesday, November 4th we had Grace Kelemanik do a presentation and a workshop for the teachers in our project intended to offer ways to use the standards for mathematical practice to support English-language learners (ELL) and students with special needs.

Introducing the ideas

As the picture above suggests, Grace does not consider all the mathematical practices from the Common Core as being equal in importance. In particular, she sees MP2 (Reason abstractly and quantitatively), MP7 (Look for and make use of structure), and MP8 (Look for and express regularity in repeated reasoning) as being potential pathways students can use to solve mathematical problems. 

If you want to support students in using MP2 to solve problems, consider the following questions:

• What can I count or measure in this problem situation?
• How do the quantities relate to each other?
• How can I represent this problem?
• What does this (expression, variable, number, shaded region, etc.) represent in the problem context?

If you want to support students in using MP7 to solve problems, consider the following questions:

• What type of problem is this?
• How is this (situation, object, process, etc.) connect to another math idea?
• Is it behaving like something else I know?
• How can I use properties to uncover structure?
• How can I change the form of this (number, expression, shape) to surface the underlying structure?
• Are there “chunks”?

If you want to support students in using MP8 to solve problems, consider the following questions:

• Am I doing the same thing over and over again?
• Am I counting in the same way each time?
• Do I keep doing the same set of calculations?
• What about the process is repeating?
• How can I generalize this repetition?
• Have I included every step?

These questions come directly from Grace’s presentation and are likely to be included (along with more examples) in a book Grace and her co-authors (Amy Lucenta and Susan Creighton) hope to complete soon. The questions remind me of the general problem solving heuristics that George Polya developed, but with a greater level of specificity, perhaps one that students can generalize to any problem context themselves.

Modelling the practices

In the afternoon, Grace modelled some of the practices she talked about in the morning and in particular focued on how a lesson focused on using MP7 could help students make sense of the mathematics being demonstrated. It is worth noting that my description below is based on my memory of what happened (I did not take detailed notes) and so hopefully I have represented Grace’s work well.

Grace started by showing something similar to the following expressions:

• 3×4 + 9×3 + 9×3 + 5×3
• 2×(9×3) + 9×4
• 5×10 + 2×(3×4) + 4×4

She described what the purpose of the activity was, and then uncovered three diagrams (similar to the ones below) which she said corresponded to the calculations of area already given. The fourth diagram she uncovered later.

First she asked someone in the audience to explain which expression corresponded to the first diagram. While someone explained why the diagram and the expression were related, she carefully underlined the “chunk” of the expression which corresponded to the “chunk” of the diagram and shaded in the related portion of the diagram using the same color.

She then asked students to work with a partner to figure out which expression corresponded to the first diagram and why. Once students (in this case our teachers) had time to work this out, she asked two different pairs of students to come up to explain their reasoning. One partner was allowed to point but not talk and the other partner was allowed to talk but not point. Together they had to explain how they found a relationship between the expression and the diagram and color in the diagram and underline the expression in the same way. Grace repeated this process three times, once for each diagram.

She unveiled the blank diagram and asked participants to think of another way of cutting it up and then constructing the corresponding expression for their version of the diagram. She had someone come up to explain another way of looking at the expression using the blank diagram and construct their own corresponding expression, again asking them to ensure that they used color to relate the diagram and the expression.

Finally she summarized what each group found and asked if anyone saw any generalizations they saw between the different solution methods that were used.

Further support for students

Grace then went on to articulate five instructional strategies she used during the workshop that help support students in understanding the mathematics.

• Think-Pair-Share
• Annotating
• Sentence Starters and Frames
• Repetition
• Meta-reflection

She ended her presentation with this terrific comic from Michael G. Giangreco.

(source)

My reflection

Grace’s workshop took place in a room with about 130 teachers and I observed the diagrams from the opposite corner of the room. What I noticed is that even though I could not hear everything that was said, I was still substantially able to follow the mathematical arguments being made. I attributed my ability to follow the mathematics to the strategic use of color, the repatition in the diagrams, the use of gestures by Grace and the “students” who came up to present, and of course my existing understanding of the principle being focused on.

I also noticed that at no point did anyone actually talk about or calculate the final area. It was not that the final area was not important but that in this context, my suspicion is that it would not have contributed to the conversation, which was focused on the strategies and processes one could use to find the area. Grace was also careful not to introduce “the best way” to cut up the diagram to focus on students making sense of the relationship between the different ways of slicing up the shape given and the expressions given.

Students were not expected to come up with their own way of cutting up the area (which in my experience many students find challenging) or of creating an associated expression until they had listened to three different representations and been required to think about each diagram themselves.

A follow-up activity

As the workshop unfolded during the day, I thought of an activity that one could do on their own to follow up on the first part of the workshop. The purpose of this activity is two-fold; to understand different approaches to solving mathematics problems and to better understand the standards for mathematical practice.

Take a given mathematics problem (like this one) and construct a solution that emphasizes the use of MP2, another solution that emphasizes the use of MP7, and yet another solution that emphasizes MP8. Look at all three solutions and look for similarities and differences between the solutions. Think about how you would support students in understanding how to construct any one of the solution pathways you constructed (or in supporting students to construct their own solution pathways using MP2, MP7, or MP8).

Update: Here’s an example of the same task done in three different ways.

I solved the same task three different ways, attempting to use SMP2, 7, and 8 respectively. Thoughts? #mathchat pic.twitter.com/m8LY3QJQug

— David Wees (@davidwees) November 10, 2014

I’m facilitating a pair of workshops this weekend in San Francisco, both of which are fairly self-directed workshops. In fact, it occurred to me that a motivated person or small group could probably get a lot of out of what I have constructed without my direct support. So I’m embedding them below. Feel free to use/share these resources (for non-commercial purposes). In each presentation, there is a link to the folder that holds the agenda for the workshop, and that agenda contains a link to the folder of associated resources.

If you are reading this blog post and do not see the slides embedded above, try reading it here instead.

I’ve been thinking a lot recently about what knowledge is needed by mathematics teachers in order to be excellent teachers. It is clear to me that teachers of mathematics must know the mathematics they are to teach, but what else do they need to know?

(Source: Content Knowledge for Teaching: What Makes it Special?)

I’m not the first person to wonder this. In a 2008 paper, Deborah Ball, Mark Thames, and Geoffrey Phelps describe a categorization of the mathematical knowledge needed for teaching into five broad types, described in more detail below.

Knowledge of mathematics

• Common mathematical knowledge:

  Deborah Ball et al. describes this as “knowledge that we would expect a well-educated adult to know” (Ball, Content Knowledge for Teaching. What makes it special?, 2008). It is closely associated with the curriculum that is being taught and includes knowledge of when students are making mistakes and when there are errors in a textbook.

  For example, common mathematical knowledge includes knowing how to subtract a negative number from a positive number. It includes knowing how to multiply multi-digit numbers together. It includes knowing how to solve a quadratic equation by factoring. It includes all of the mathematical knowledge necessary to solve mathematical problems in at least one way.

  Note that teachers should at least know all of the common mathematical knowledge they are expected to teach as well as how that knowledge is connected to the mathematics students are likely to learn later in school. If I teach my students that an equals sign (=) means “find the answer” they are likely to find algebra confusing until they learn that the equals sign means “the two expressions on either side of this = sign are equal in size”.

  
  (Source: Finding a percentage)

  Notice in the example above, the author of this video is dividing 4 by 16. Instead of making sense of the calculation, he starts by following the algorithm which results in a non-sensical calculation. Someone who understood this division calculation with a stronger conceptional understanding might realize that since 16 is larger than 4, we can skip the first iteration of this division calculation and move straight away into 40 divided by 16.

  When teachers lack this mathematical knowledge, they often end up relying on tricks instead of mathematical understandings. In my own practice, I remember when I was first called upon to teach the Chi-squared test, which at the time I did not know. I read ahead in my textbook and figured out how to follow the mathematical recipe that produced the Chi-squared calculation well enough to muddle through it in class. However years later I finally connected the expected values to probability and realized that I had for many years missed an opportunity to help students make a connection between this test and other things we were learning that year.

• Specialized mathematical knowledge:This is “knowledge beyond that expected of any well-educated adult but not yet requiring knowledge of students or knowledge of teaching” (Ball, 2008). For example, knowing some of the many different representations of positive and negative numbers is mathematical knowledge that one could not expect every well-educated adult to know, and does not require knowing students or teaching.

  An example of specialized mathematical knowledge is knowing how to represent subtracting a negative number from a positive one in a variety of different ways. Since different students are likely to find different models for understanding current topics more or less easy to grasp, it is incredibly useful to know a variety of different ways of representing and approaching each area of mathematics that is taught.

  
  Different models for understanding subtracting negative numbers

Knowledge of students:

• Pedagogical content knowledge
  • Knowledge of the ways students understand the content:This is the knowledge of not just the ways to do mathematics but the ways in which students understand the mathematics. While some mistakes students make are the result of over-taxed memory or carelessness, not all mistakes students make can be explained in these ways.

    
    (Source: Math Mistakes)

    What mistake did this student make above? What does this mistake mean they were thinking when this did this calculation? How would you help this student? Answering all three of these questions requires an understanding of the ways student understand this mathematical content.

    Magdalene Lampert once told me the story of an interaction she had with a 5th grader. Near the very end of a class discussion, he said that 0.007 is negative. The class ended and Magdalene was left to try and figure out why the student thought that 0.007 is negative. If teachers have the common mathematical content knowledge they need, they should understand that 0.007 is not negative. If teachers have sufficient knowledge of the many different ways students might understand mathematics, then they will know that there is a fairly logical (although incorrect) train of thought that leads students to the mistaken understanding that 0.007 is negative. Any guesses as to what this student was thinking?

  • Knowledge of the ways to teach mathematics:This is the knowledge of how to teach mathematics so that it makes sense to someone else. It includes thinking about the sequencing of mathematics concepts as well as knowing rationals for why various pieces of mathematics are correct. Teachers need to make choices about what mathematical representations to use with students and which of those representations are likely to understood and misunderstood by students.

    In my previous example, knowing the different models of understanding the mathematics is specialized mathematical knowledge, knowing which models to choose and how to sequence the models is mathematical knowledge for teaching.

    
    Different ways of representing 12 times 6

    These are a few of the different models for understanding multiplication. Which of these models do you think work best for initially introducing multiplication? Which of these models is most efficient? How are these models connected to each other?

    
    (Source: Jason Zimba, NCTM 2014)

    When teachers do not know how to teach a particular idea to students in ways that make sense to students, they may rely on mnemonics or other non-mathematical ways for students to remember mathematical content. If you look at the example above, it is clear that whoever created these diagrams is hoping that these will help students remember the math facts for 3×3 and 3×4. Wouldn’t it be better though for students to understand at least these simple multiplication facts based on pictures of what they represent or at least be memorizing the words that represent this relationship?

    This area of knowledge also includes how to ask questions in class that get all students thinking, how to give students feedback that helps them move forward, and how to choose instructional activities that support students learning mathematics.

  • Knowledge of the curriculum:Teachers also need to know the scope and range of the mathematics they are teaching. They need to know the standards that are appropriate for their particular course as well as what those standards mean. They need to know what resources they have available as well as how useful those resources are for their teaching. They need access to curricular resources and because of the limited time teachers typically have available to plan, they need to know where to find the resources they need without spending an enormous amount of time searching.

There is other knowledge teachers need to know outside of the knowledge related to their content area.

Knowledge of students and schools

• Knowledge of students’ cultures and backgrounds:While this is not typically included in the lists of knowledge required for teaching, it is pretty clear to me that it is necessary. The ignorance that led this group of NYC teachers to not only wear these t-shirts but to also pose for a photo is a clear sign that there is a body of knowledge about students’ culture and teachers’ impact on it that exists and that not all teachers know.
• Knowledge of the emotional needs of students:Teachers are also responsible for understanding the emotional needs of the children under their care. These needs change over time and are different for different children. Teachers need to pay attention to the status needs of their students and to understand how status impacts their classroom instruction.

  Who can be grouped with whom? Who looks like they need more support today? Which children look like they are being abused or neglected? Who is likely to be excited by today’s lesson?

• Knowledge of the rules and procedures related to teaching:Every school has procedures teachers are expected to follow and every country and state has laws teachers are expected to obey. While knowledge of these rules and procedures is completely insufficient to be able to teach, a lack of knowledge of these rules and procedures has led many educators to disaster.

Conclusion:

From my own experience, I learned very little of this before I started teaching, aside from the knowledge of most of the mathematics I was employed to teach. During the course of my career as I attempted to make sense of what students understood and planned lessons to build student mathematical knowledge, I slowly built up my understanding of these areas of knowledge.

(Source: Embedded Formative Assessment)

The graph above shows a summary of research on the correlation between how many years of service literacy and numeracy teachers have compared to how much their students learn. Early in their careers, both teachers of literacy and numeracy struggle to use the knowledge they have to successfully teach students. One way of interpreting the graph above is that as they progress through their careers, both teachers of literacy and numeracy increase their knowledge of how to teach, and their students benefit.

What of the knowledge above can teachers begin to learn before they start teaching? How can we ensure that every teacher of mathematics learns enough of this content during the course of their career in order to be able to teach? Also, how does this post relate to teachers of other content areas or elementary school teachers?
References:

Ball, D. L., Thames, M. H., & Phelps, G. (2008). Content knowledge for teaching what makes it special?. Journal of teacher education, 59(5), 389-407.

Wiliam, D. (2011). Embedded formative assessment.

The objective of this list is to identify a core set of teacher practices that every teacher should do. There are some things missing from my list. For example, I have not highlighted the need for every teacher to be aware of issues around the social status of their students, their students emotional needs, or have a certain level of cultural awareness. I think these things are important, but I’m not sure how to describe them in a sentence. If you have any suggestions…

I’m also fully aware that these sentences are probably too brief to be a complete picture of the complexity of teacher practice. There are entire books on giving good feedback and understanding formative assessment. I do not view this list as a simple check-list but rather as a starting place for teachers and teacher-educators to ask questions about effective teaching practice.

I’m sharing this graphic with a Creative Commons Attribution, Non-commercial, Share-alike license. You can make a copy to modify it here if you like, provided you make any changes from the original obvious, and provide appropriate attribution. Also, here is a PDF version.

What else would you include? What do you disagree with? Do you have any clarifying questions about what I mean by anything on this list?