The purpose of this post is to show an example of using math in the context of programming. I’ve written the post as I created the project, to try and outline my thinking during this process as much as I can. This is an example of me applying math that I know to a different context, creating a spiral of numbers. In a future post I plan on exploring what learning new mathematics through programming could look like.
Note: This post will look much better in the online version if you are reading it in an RSS reader or your email.
First, I start with a pretty basic HTML file with some an embedded JavaScript library called jQuery, and a blank Canvas HTML element.
[html5]
Prime Spiral
[/html5]
In the Javascript file, I start with the following:
// init()
$(document).ready(function () {
});
// debugging function
function debug(message) {
$(‘#debug’).append(message + ‘
‘);
}
So far all I have done is create two template files (which I always create when I am starting a new project written in JavaScript), and I have added the minimum skeleton to both of these files to get my project started.
// settings
var settings = {};
settings.numberOfNumbers = 200;
At the beginning of the JavaScript file, I add a settings variable. This will allow me later to tweak my project settings in one central location, rather than having to find where I have an embedded setting and modify it.
Next, I decided to resize the canvas so that regardless of what browser will view the canvas, it will be visible in their browser window.
// resize the canvas to the minimum of height and width for the screen
function resizeCanvas() {
// get the new width of the canvas, which should be the minimum of the height or width of the page
settings.dimension = $(window).height() > $(window).width() ? $(window).width() : $(window).height();
// now shrink it slightly
settings.dimension = settings.dimension * 0.90;
// now resize the canvas elements
$(‘#theContainer’).css({‘height’: settings.dimension, ‘width’: settings.dimension});
$(‘#theCanvas’).css({‘height’: settings.dimension, ‘width’: settings.dimension});
}
There are two pieces of mathematics here. One is a comparison between the height of the browser window and it’s width, and the other is shrinking of the region to 90% of the original dimensions. I could have used the built in minimum value function for the first part, but for some reason, I chose not to.
The next step is to actually write the numbers in a spiral. To do this, I decided to work in polar coordinates, because spirals are convenient to draw in that coordinate system, but unfortunately browsers operate in Cartesian coordinates. Each point in the browser window can be labelled with an x, y position, as measured from the bottom-left corner of the canvas. My objective is to start numbering the spiral from the center of the canvas, so I will have to translate each point, after having converted from polar coordinates to rectangular coordinates.
Here is the function for the conversion:
// convert from polar coordinates to offset cartesian coordinates
function convertFromPolarToCartesian(radius, theta) {
// A point at (radius, theta) can also be thought of as being
// at the end of the hypotenuse of a right-angled triangle,
// hence we can use trigonometry to find the Cartesian coordinates.
// Note: theta will need to be in radians to be useful here, since
// the Math.cos() and Math.sin() functions assume the angle is in radians.
var x = Math.cos(theta)*radius;
var y = Math.sin(theta)*radius;
// now shift the point into the center of the canvas
x = x + settings.dimensions/2;
y = y + settings.dimensions/2;
// return both points as an array
return new Array(x, y);
}
Now comes a moment of truth. I have not yet been able to test these most recent functions I have created, so they may have mistakes in them. I need to actually attempt to use these functions to find out if they return the expected values. My next step is to therefore try and produce a function which will create the spiral of numbers, using the functions I have so far as tools. First, I want to cycle through all of the numbers, which looks like this:
// draw the spiral of numbers
function drawNumbers() {
// cycle through each number from 1 to the maximum number of numbers given
for (var index = 1; index <= settings.numberOfNumbers; index++) {
}
}
This is essentially a sequence of numbers where I start with a value of 1, and I increase them (using index++), until I reach the maximum value as set globally in the script.
With each of these numbers, I am now going to want to calculate what it’s position would be, remembering that I’m going to work in polar coordinates. I want the radius of the position of the numbers to slowly increase in a linear way, from an initial value of zero, to a maximum value of just less than half of the maximum width of the canvas. Therefore when the number is 1, this should map to a radius of zero, and my maximum number should map to my maximum radius. Here’s my initial guess as to what this conversion should be:
radius = (index – 1) / settings.numberOfNumbers * (settings.dimension / 2) * 0.90;
For the angle, I just want it to increase at a constant rate for each number, remembering that I will be working in radians. An increase in angle of $\frac{1}{32}$ of a full rotation of a circle seems like a reasonable initial guess.
theta = (index – 1) * (1 / 32) * Math.PI;
Next, I used the function I created earlier to convert into Cartesian coordinates (with the shift), and finally I created a function which should actually display the numbers on the canvas. Here is what the full spiral function looks like at this stage:
// draw the spiral of numbers
function drawNumbers() {
// define the variables
var radius, theta, coordinates;
// cycle through each number from 1 to the maximum number of numbers given
for (var index = 1; index <= settings.numberOfNumbers; index++) {
// set the radius so that it increases as the index increases, but is initially zero
// note that we also want to scale the radius down slightly so that our spiral
// is slightly smaller than the canvas
radius = (index - 1) / settings.numberOfNumbers * (settings.dimension / 2) * 0.90;
// our angle should increase at a constant rate, starting at 0
theta = (index - 1) * (1 / 32) * Math.PI;
// now convert these into Cartesian coordinates
coordinates = convertFromPolarToCartesian(radius, theta);
// and then actually draw this number
drawNumber(index, coordinates.x, coordinates.y);
}
}
Here’s the output of this function.
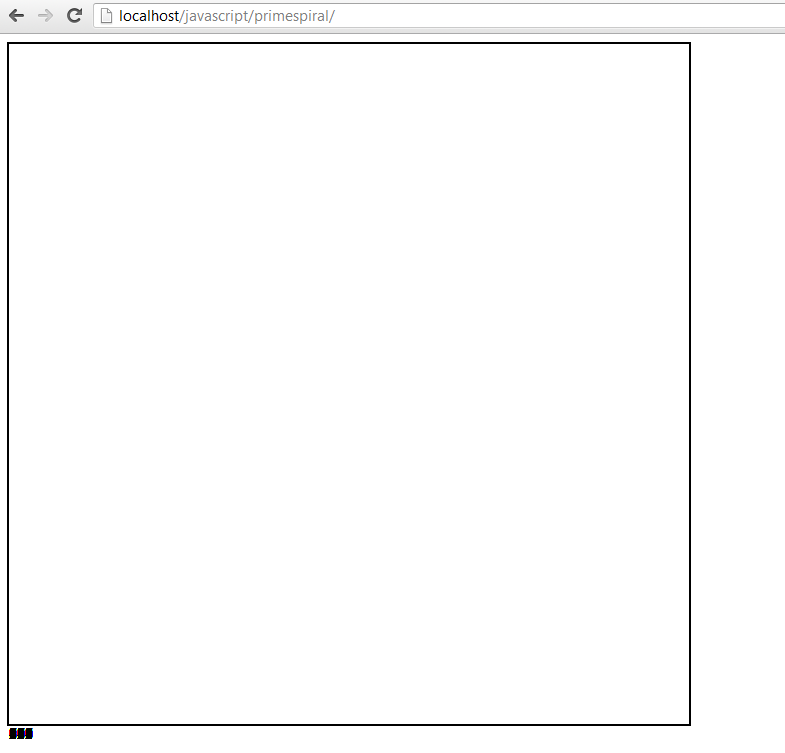
Ooops! Something went wrong. I scanned through my code, and luckily I spotted my mistake quickly. I had included an extra “s” in my polar coordinates to Cartesian coordinates conversion function. Here’s the updated output. This process of debugging a mistake can sometimes be quite frustrating, so it requires developing patience.
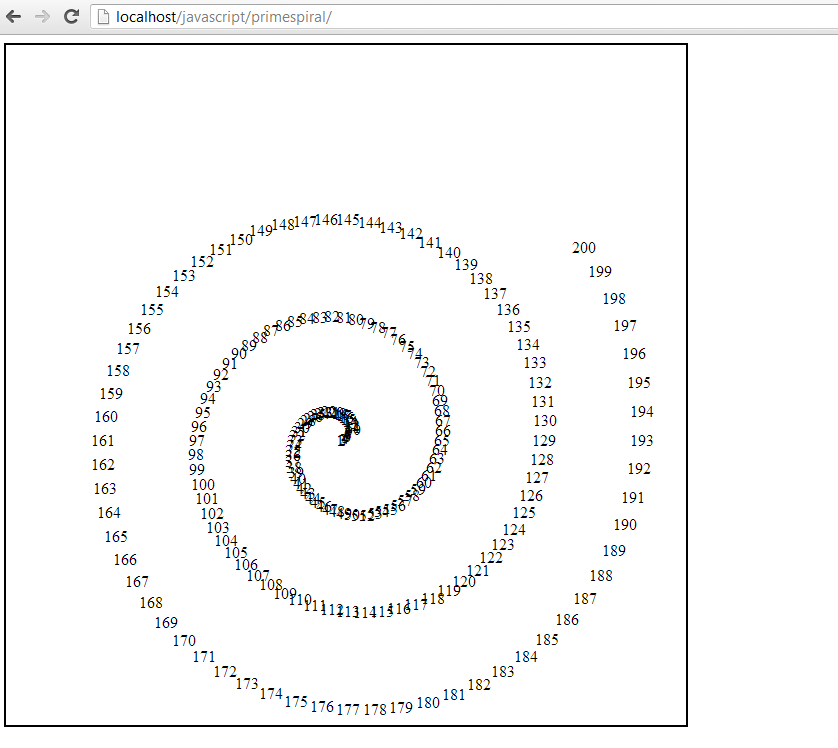
It is clear that my basic concept works at this stage. The numbers look very tightly jumbled at the beginning, which is probably because the angle rotation isn’t sufficient early on. My assumption that a linear increase in angle would work is probably wrong. Also, the spiral isn’t centred inside the canvas, suggesting that I will want to work on my conversion function.
I want the angles to start spread out more than they are, and then slowly increase over time. I tried some of the following, none of which produced the desired effect.
// tried varying the fraction increase of the angle
theta = (index – 1) * (1 / 16) * Math.PI;
// tried using a reciprocal function for the angle
theta = (index – 1) * (10 / index) * Math.PI;
// tried using a reciprocal square root function for the angle
theta = (index – 1) * (10 / Math.sqrt(index)) * Math.PI;
// trying a decay function on the angle
theta = (index – 1) * (Math.exp(-1*index/100)) * Math.PI;
I realized at this stage that what I wanted was not a constant increase in the angle, but a constant distance between the points, after their conversion into Cartesian coordinates. I decided to try and draw this out on paper to see if I could work out an algebraic relationship. I decided then to draw the following diagram to see if it would give me any insights on how to proceed:
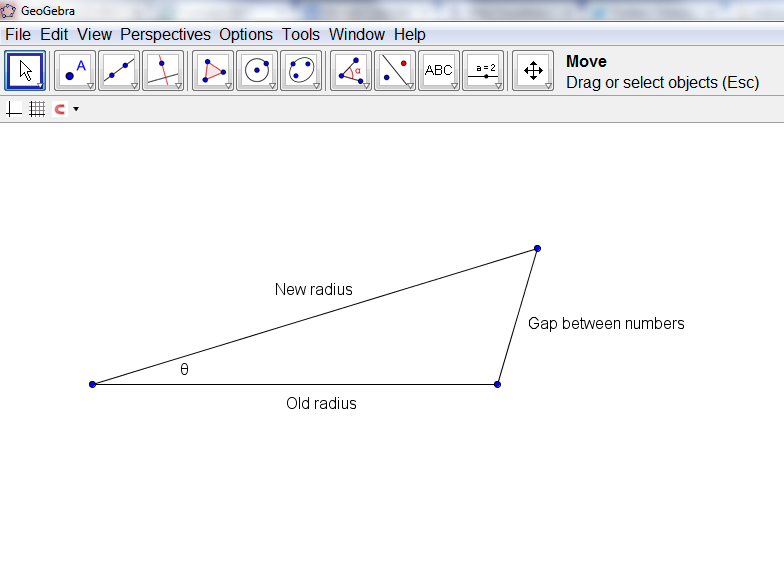
When I looked at this, I realized that I could use the Cosine law to find the angle, given the new radius, old radius, and the gap between the letters. Initially, I tried a constant gap between the numbers, but after some playing around, I decided to gradually increase the font size between the numbers, and at the same time, gradually increase the gap between the letters. I ended up settling down on this as my final set of formulas for determining the position of the numbers.
// draw the spiral of numbers
function drawNumbers() {
// define the variables
var radius, radiusnew, rhs, theta, coordinates, fontSize;
// cycle through each number from 1 to the maximum number of numbers given
for (var index = 1; index <= primespiral.settings.numberOfNumbers; index++) {
// set the radius so that it increases as the index increases, but is initially zero
// note that we also want to scale the radius down slightly so that our spiral
// is slightly smaller than the canvas
radius = (index - 1) / primespiral.settings.numberOfNumbers * (primespiral.settings.dimension / 2) * 0.90 + 10;
// keep track of the old radius
radiusnew = (index) / primespiral.settings.numberOfNumbers * (primespiral.settings.dimension / 2) * 0.90 + 10;
// fontsize should increase linearly as the index does
fontSize = Math.round((index) / primespiral.settings.numberOfNumbers * 10 + 10);
// calculate the rhs of the cosine law
rhs = (radius*radius + radiusnew*radiusnew - (fontSize*1.5)*(fontSize*1.5))/(2*radius*radiusnew);
// ensure that there is a minimum radius
if (rhs < 0) {
rhs = 0.1;
}
// our angle should increase such that the distance between the numbers is kept constant;
theta = Math.acos(rhs);
// now convert these into Cartesian coordinates
coordinates = convertFromPolarToCartesian(radius, primespiral.currentAngle);
// increment the next angle
primespiral.currentAngle += theta;
// and then actually draw this number
drawNumber(index, coordinates.x, coordinates.y, fontSize);
}
}
How this works is that it calculates the current radius, the radius of where the next number will be placed, and then calculates the angle that corresponds to the gap between the letters, and then it saves all of this information for the next iteration of the loop by incrementing the current angle variable. I also worked on the portion of my script that converts the polar coordinates into Cartesian coordinates in an effort to better centre the spiral. This is my output with this code:
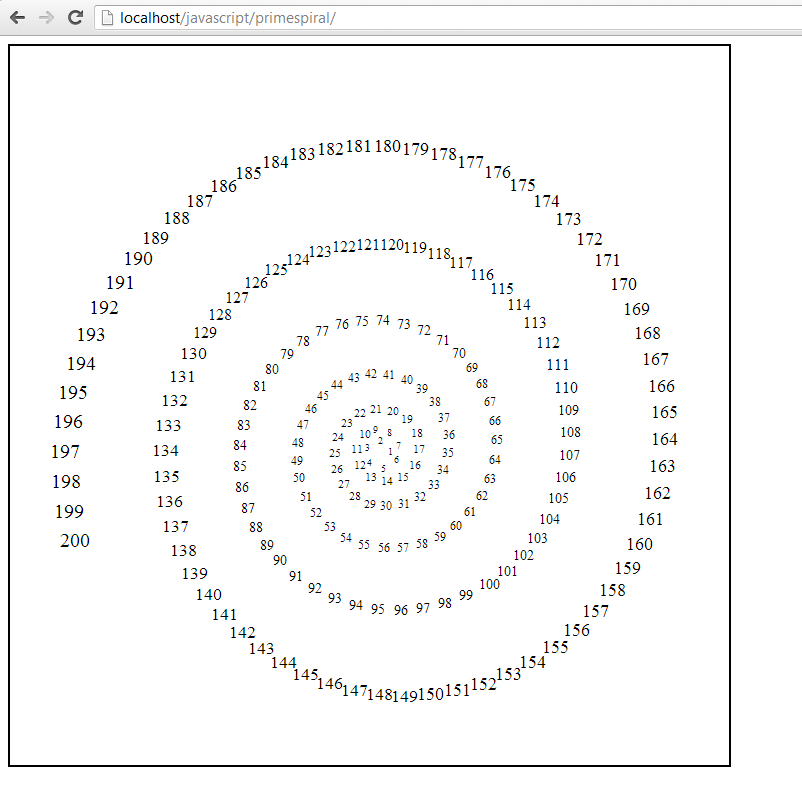
I decided, somewhat arbitrarily, that the next step is to identify which of the numbers are prime, and highlight them in some way to make them distinct. This means that I needed to write a function to determine if a given number is prime, and then pass along this information to the function that draws the numbers. Here was what I ended up with. Note that this function actually doesn’t work completely (except for “small” numbers) as noted in the comment at the end.
// identifies if a given number is prime or not
function isPrime(number) {
// naive algorithm
var primes = new Array(
2,3,5,7,11,13,17,19,23,29,
31,37,41,43,47,53,59,61,67,71,
73,79,83,89,97,101,103,107,109,113,
127,131,137,139,149,151,157,163,167,173,
179,181,191,193,197,199,211,223,227,229,
233,239,241,251,257,263,269,271,277,281,
283,293,307,311,313,317,331,337,347,349,
353,359,367,373,379,383,389,397,401,409,
419,421,431,433,439,443,449,457,461,463,
467,479,487,491,499,503,509,521,523,541,
547,557,563,569,571,577,587,593,599,601,
607,613,617,619,631,641,643,647,653,659,
661,673,677,683,691,701,709,719,727,733,
739,743,751,757,761,769,773,787,797,809,
811,821,823,827,829,839,853,857,859,863,
877,881,883,887,907,911,919,929,937,941,
947,953,967,971,977,983,991,997,1009,1013);
// check to see if the number is 1
if (number == 1) {
return false;
}
// first check to see if our potential prime is in the list
for (var i = 0; i < primes.length; i++) {
if (primes[i] == number) {
return true;
}
}
// now check every prime smaller than n
for (i = primes.length - 1; i > 0; i–) {
if (number % primes[i] == 0) {
return false;
}
}
// this isn’t actually guaranteed, unless n < 1013*1013
return true;
}
Putting all of this together, and I end up with this. You can view the entire JavaScript file here.
What mathematics did I end up using? Do you think that this kind of application of mathematics would be a valuable one for students to experience?