I introduced matrices to my students last week. Together, we worked out the algebra necessary to find the inverse of a 2 by 2 matrix, and developed the idea of the determinant of the matrix. The algebra was hard for my students, and we focused on looking for patterns. I showed students how a matrix can be applied to solving simultaneous equations, so they understood that there is some context for matrices. Next week, I intend to show some of the applications of matrices to game theory, and have students explore the consequences of this application.
Today, I talked about the inverse of a 3 by 3 matrix, which was easily found on a calculator. However, for good or for ill, students are expected to know how to find 3 by 3 matrix inverses "by hand" in preparation for their IB Math SL exam. So we needed a way to understand how the inverse of a 3 by 3 matrix is formed. I showed students that one can construct 2 by 2 matrices within the 3 by 3 matrix, and that the determinants of these 2 by 2 matrices "magically" appear in the inverse of the 3 by 3 matrix. The proof of this (for 11th grade students) is hard.
So instead of going through the proof, I decided that students should explore the relationships between the positions of the 2 by 2 embedded matrices, and where their determinants appear in the 3 by 3 matrix. I don’t myself have an intuitive sense of exactly where these determinants will show up, but I know there is a pattern, and that my students will find it.
What was fascinating to me is the different ways students represented the notation necessary to show these patterns.
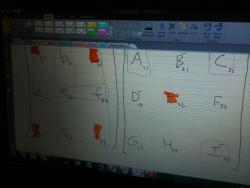


Examples of student notation. Click to enlarge.
Each student came up with their own notation to represent the patterns they were finding. They realized (some of them with some guidance) that it was pretty critical to include the location of the 2 by 2 matrix in their notation, to make it easier to find patterns. The actual notation they use doesn’t matter to me, as if they do continue with matrices, they’ll learn the appropriate notation later. What was critical for me was that they could come to some understanding of how to find the inverse of a 3 by 3 matrix.
What I found most interesting about this activity is that there is room for exploration in learning matrices, which suggests to me that it is very likely that any mathematical topic has some opportunity for exploration.