Last Saturday, I tried a new instructional activity called Choral Counting. This activity was recommended to me by Magdalene Lampert and comes out of the work she and others have done to support high-quality ambitious teaching.
I’m experimenting with these instructional routines in part because I hope to support teachers in the project I support in using them in their instruction, which I can hardly be expected to do without experiencing them from the inside myself. It’s clear that this activity is much richer mathematically than one might expect from just hearing about it. One finding I have already is that I have to do a much better job of planning how I will use my space when recording the numbers!
The basic idea of choral counting is easy — students count in unison and you write down the numbers as they chant, and then pause students to ask them questions about the numbers. What I learned Saturday is that there is a lot of potential in this activity to bring out rich mathematical ideas for discussion as a group.
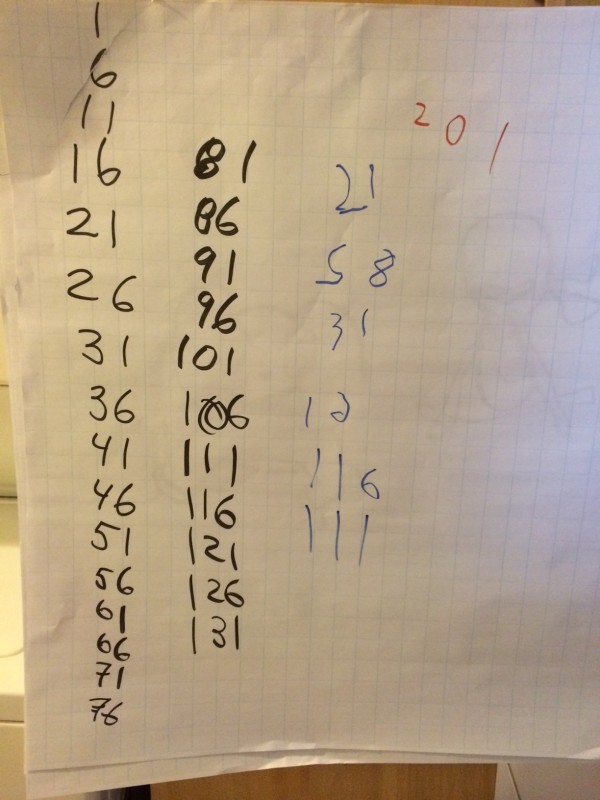
I chose to start at sixteen and count by fives. While the counting was going on, I noticed my students paused a bit at 76. So I stopped and asked them why they think they paused. They also paused at 101, which during my lesson planning I had anticipated they would do. They also had different responses at 111 (121 was next, which I expected).
I don’t know why they found 76 more challenging. Maybe because it was the first time they had to use a number in either position higher than 6? 101 is clear – Many students thought “tendy one” and self-corrected before they spoke, which slowed them down. I thought this myself when I first counted through this routine! Many students said 121 instead of 111 and I remember my own son doing something similar when he was learning how to count. I also paused a couple of times to ask students what pattern they noticed and at one point I asked them to predict what the number would be if we counted four more times. One student proved her answer by counting up by fives, another student said it would be twenty more because four times five is twenty.
Here’s the data collected by my assistant teacher (one of the children’s older sister comes to the class and she has happily volunteered to record information for me and to walk around the class generally supporting students).
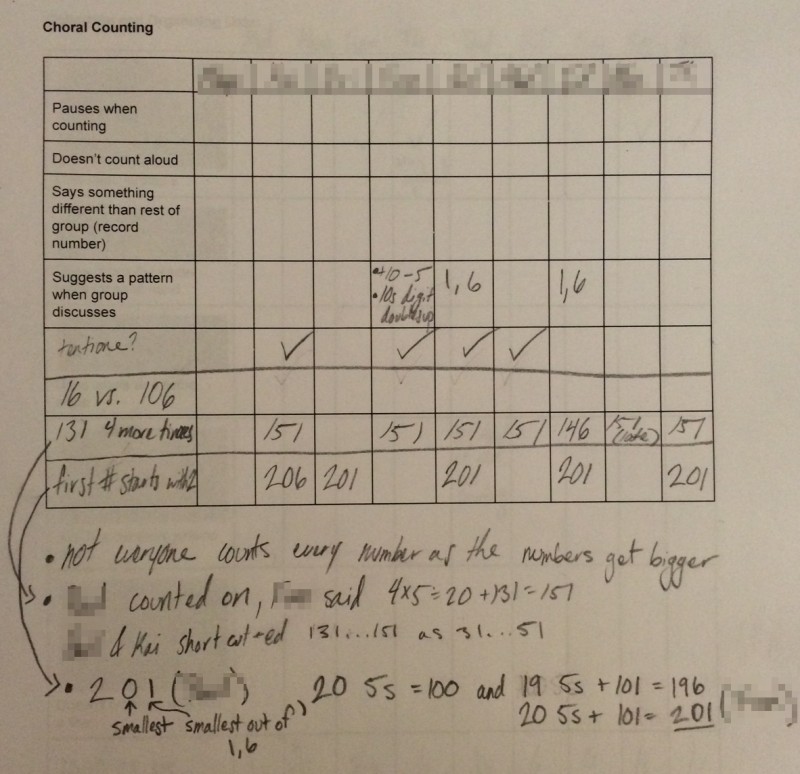
Once we got to 131, I asked students what would be the next number that starts with 2. Two students came up with different mathematical arguments that the next number would be 201. One student said that the first digit was clearly a 2 and that the next digit must be a zero, because we are counting by fives. The last digit must be a 1 because our pattern always alternates between 1 and 6 and 1 is smaller than 6. The other student said that if we counted 19 fives or 95 higher from 101, that would be 196 which does not start with 2, but that if we counted 20 fives or 100 higher from 101, that would be 201 which must be the next number starting with 2 since we won’t count a number between 196 and 201.
Although the activity went longer than I expected, it was incredibly rich and worth doing.