Source: NCTM Smartbrief
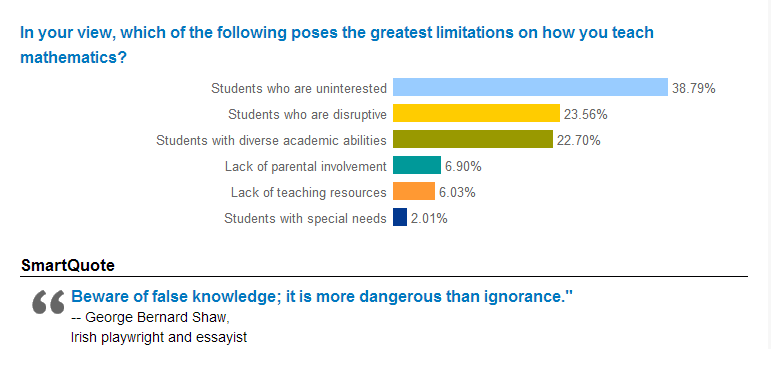
It seems to me that "students who are uninterested" is a problem of pedagogy. If that is what is holding students back from learning mathematics, then you should make your lessons more interesting. "Students who are disruptive" seems like another way of phrasing the first problem, but having worked in a challenging school myself, I do remember students who were challenging no matter how much I stood on my head to make my lesson interesting. That being said, both of these challenges are significantly less with good teaching. Students who are uninterested in what you teach are a sign that you should change your approach.
"Students with diverse academic abilities" is a serious problem, but it is (at least in part, see below) solvable. The basic trick is this, don’t teach everyone the same thing at exactly the same time. I would approach this particular issue with low-entry / high ceiling problem solving activities in small groups and then I workshop solutions with individual groups as I move around the classroom.
"Lack of a parental involvement" is definitely a huge issue. I think if you have interesting lessons and develop positive relationships with your students though you can mostly counteract the effects of parental apathy. My objective here is to set high standards for my students and their relationship with math like what I have for my own son.
"Lack of teaching resources." Uh… Have you heard of the Internet? Being a part of the Math Twitter Blogosphere means that lack of resources is never a problem. In fact, more resources than I can possibly use is more frequently the problem. Edit: It occurred to me that this may mean lack of physical resources, like pencils and paper, etc… in which case someone, somewhere, needs to rethink the priorities for their schools. Teachers and students should not lack for basic supplies.
For me the "students with special needs" problem can partially be addressed with using a problem solving approach with media that asks questions (like what Dan Meyer is curating with 101qs.com) for students for whom literacy is their barrier to mathematics. However, students with dyscalculia or who are many, many grade levels behind in their understanding of mathematics probably need more support. Having worked in a school that had minimal support for students with special needs many years ago, I definitely empathize with people who see this as a problem.
The thing is about all of these responses is that not one of them is how I would answer this problem. For me, the things that I feel impose the greatest limitations on how I would teach (and most importantly, what I would teach) are the standards we are assigned to teach and the way students will be eventually externally assessed on those standards. I can certainly still teach in a creative way given these limitations, but they definitely place limitations on how I teach.