Designing an interesting and open-ended task is relatively easy. The challenging part comes when you attempt to use the task and learn something as a teacher about what your students understand.
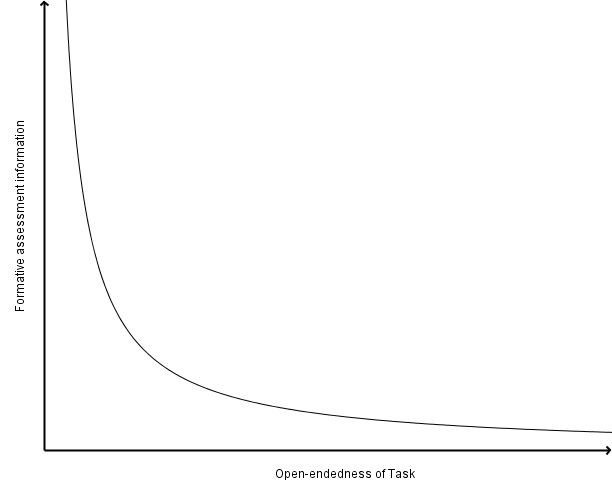
This graph represents the main issue that comes up when designing open-ended tasks for students to use; the more open-ended a task is, the less information you are likely to be able to gain from using the task. You can gain insight into what your students are thinking when they are working on an open-ended task, but chances are much greater that they have a much wider variety of insights and misconceptions that will come up during their time working on the task.
If we define "formative assessment" as "any tool used by teachers to gain insight into their student’s thinking and use that information for future planning of teaching and learning activities," then the open nature of these tasks helps with gaining insight into student thinking, but it makes planning future activities more challenging since we could potentially end up with much more information about what each student knows how to do, but potentially less information about what each student does not know how to do.
The very task that gives students the freedom to try many different potentially successful mathematics techniques to solve the problem unfortunately also limits how much of what we know of those paths that students chose not to follow. Did a student not use an algebraic approach because they don’t know algebra? Or did they use a non-algebraic approach because they didn’t think of an algebraic technique? Did they use a table to solve the problem because they love using tables? We have no time-efficient way of answering these questions.
One possible solution is to make sure that each time students work on a task, they have the opportunity to share their different solutions with each other. This way students who tend to use graphs to solve problems will see algebraic solutions to those same problems. Students who generally solve a problem using a table of values will see how other students used a diagram instead. By sharing different solutions created from the students amongst your class, students may be able to add to their own toolbox of methods they can use to approach problems.
The problem with this last solution is that this only works when the students are working on essentially the same problem; it will fail to work when the task is so open-ended that students have sufficient influence over the questions they ask. Maybe there are some other solutions to this problem?
In a future post, I will take a task and create different versions of it, sliding along the scale of open-endedness, and hopefully this will lead to some insights as to the challenge involved in open-ended tasks.