Day: July 18, 2013 (page 1 of 1)

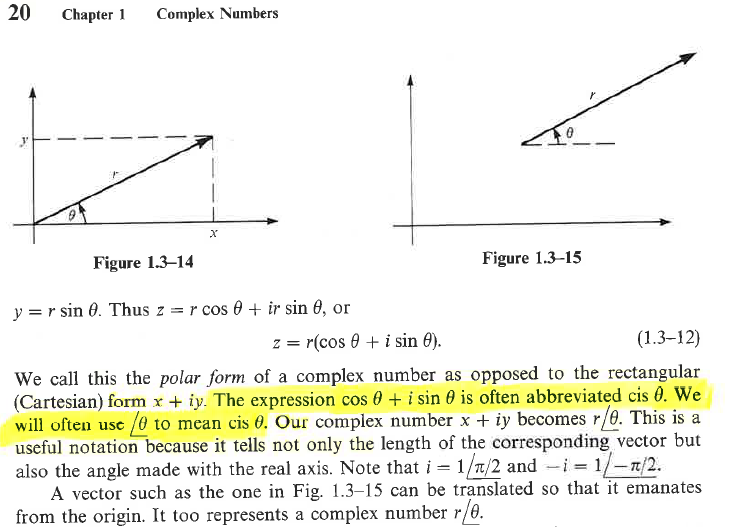
(Source: Complex Variables with Applications, Second Edition, A. David Wunsch)

I started transporting my professional books to my new office this week, five books at a time. One of the books I brought today was my old textbook from when I took Complex Analysis in university, about 20 years ago. I decided to skim through the book to see how much of those two courses I remember, and as it turns out, the answer is not much.

I stumbled upon this notation that I was unfamiliar with very early on in the textbook, and decided to work my way back through the textbook to see if I could find out where this notation was introduced, and found the only reference to a definition of the notation above.

It occurred to me that this is not so much a failure of the author, but a failure of the medium, and one that could be addressed in a digital medium much more easily. One cannot easily link to notation, especially notation used often in a traditional textbook, back to it’s origin. However in a digital textbook every single instance of this notation could be made linkable (perhaps in an unobtrussive way so as not to be distracting) back to not only the first instance of the notation, but to carefully constructed examples of the notation in use.

On a related note, in my classroom, I try my best to introduce vocabulary and notation as it is needed to describe mathematical (or otherwise) objects that the students have been gaining some familiarity with. This way the vocabulary or notation is meeting a need; labelling something that we want to discuss, rather than being artifically introduced "because we will need to know this later."

"If some one say: "You divide ten into two parts: multiply the one by itself; it will be equal to the other taken eighty-one times." Computation: You say, ten less thing, multiplied by itself, is a hundred plus a square less twenty things, and this is equal to eighty-one things. Separate the twenty things from a hundred and a square, and add them to eighty-one. It will then be a hundred plus a square, which is equal to a hundred and one roots. Halve the roots; the moiety is fifty and a half. Multiply this by itself, it is two thousand five hundred and fifty and a quarter. Subtract from this one hundred; the remainder is two thousand four hundred and fifty and a quarter. Extract the root from this; it is forty-nine and a half. Subtract this from the moiety of the roots, which is fifty and a half. There remains one, and this is one of the two parts."

~ Muḥammad ibn Mūsā al-Khwārizmī (Source: Wikipedia)

The tools for doing algebra have evolved over the years. When Muḥammad ibn Mūsā al-Khwārizmī was working on algebra, he did all of his work in words (see above). The symbols we have invented are a different tool we use for solving algebra problems. The fundamental structure of algebra is therefore something different than either of these tools.

Can we do algebra with a computer (which is today’s new tool for doing algebra) and preserve the underlying qualities that are algebra? How does access to a computer, and knowledge of programming, change what we can do with algebra?