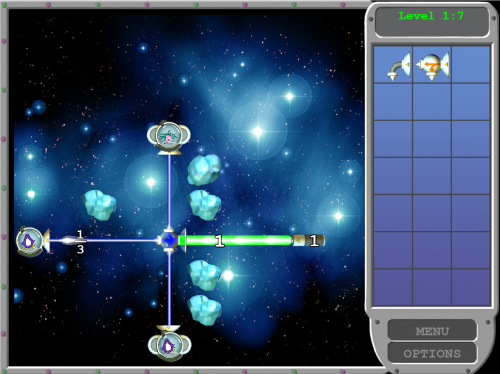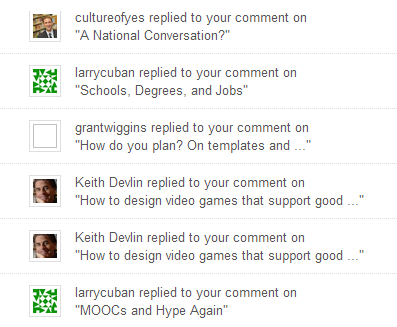
Chris Kennedy is a public school superintendent in West Vancouver, Grant Wiggins is famous for co-developing "Understanding by Design", Keith Devlin has written many books which should be relevant to the math education community, and Larry Cuban has challenged (and therefore improved or negated) education reforms for decades, and as it turns out, I happen to have replies from all four of them in my WordPress inbox right now.
If you look above, you might feel like I’m dropping names. I don’t intend this picture to convey this, rather what I want to observe is that blogging matters. Can you imagine, in the world before blogs, someone like me, a school teacher, being able to discuss ideas with the people who are driving educational change? This is not an isolated incident either. If I had chosen to capture a screen-shot of my inbox on a different day, you might see Sylvia Martinez‘s or Diane Ravitch‘s names instead.
I believe that blogging and other social media are breaking down some of our social barriers and hierarchies, but I never had quite as definitive proof until this morning.