Month: March 2012 (page 1 of 1)

March 30, 2012 / 7 Comments

Another alternative to the traditional conference

(A typical conference presentation – Image credit: Emmanuelvivier)

I’d like to propose an alternative to the typical conference model. Chris Wejr got me thinking after he sent me a message suggesting that we host a conference sometime in 2013 that he called a ‘hybrid conference’ and this post by John Burk also influenced my thinking as well.

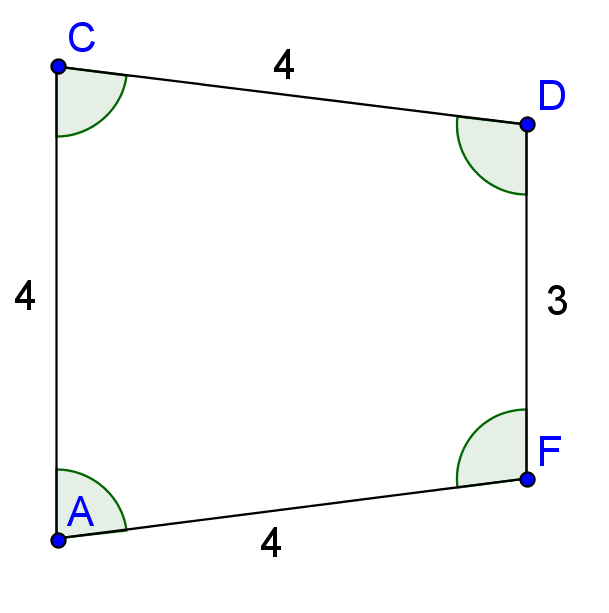
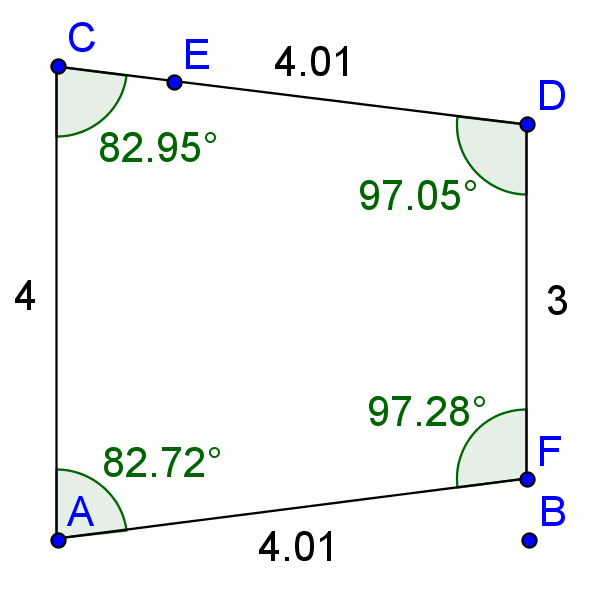
A typical conference

Some of the problems with a typical conference for many people are:

They don’t know anyone at the conference before they attend it, and so connections they could potentially make at the conference are not made,
At the conference itself, too much time is spent by presenters talking, and not enough time is spent by participants assimiliating what they learn,
Most conferences have no follow-up after the conference.

The best parts of a conference (in my experience) are:

The ability to meet and discuss ideas with other people in the same field as myself,
Being inspired by people doing amazing projects, and who give awesome presentations/keynotes,
Learning about ideas outside of our own personal areas of expertise, in other words, being pushed by others to improve ourselves.

A different conference model

First, we would assign people to cohorts (based on their interests, or on questions they answer during registration) after they register, and setting up email lists (since most people are more comfortable with email than with other social media, and it would automatically provide records of the partiicpant conversations) for those cohorts, along with a facilitator for each cohort. The job of the facilitator is to provide information to the cohort about the conference coming up, and to encourage conversation and introductions between participants before the conference. These cohorts would also be sent links to video presentations (which should be broken into small chunks and include searchable transcripts of the video) that they can watch in advance of attending the conference. Ideally, presenters would be part of these cohorts.

The people would then attend the conference, and potentially move around through their sessions (which would have to be scheduled in advance, like a typical conference, but with input from the registrations) as a cohort, with sufficient opportunities during the sessions to connect and discuss the ideas, or at least between sessions. Ideally each session would be run more like a workshop, rather than a lecture, since most (if not all) of the people in the cohort would have already listened to the presentation. In some of the more advanced sessions, participants would produce a product as a result of their time together.

Social media could be used during the presentation as a back-channel, so that people from outside of the conference could learn from the participants, and share their ideas back to the conference.

Naturally, most participants attending the conference would know some other people there. They would have conversations, and they could choose to eat together. Obviously, if one wanted to continue through the conference as a solo participant, this would still be supported by this model, one would just choose not to interact with their given cohort.

After the conference, the cohort email lists could be used for follow-up, as well as other social media. People would be expected to continue to ask questions and discuss ideas, as well as share their successes (and failures) back to the group after attempting to implement whatever strategies, techniques, or resources they learned about through the conference. Provided the participants made the effort to seek follow-up, they would have an avenue to receive it.

This conference format would help mitigate some of the problems with the typical conference format, while not taking away any of the benefits. It would further have the benefit of allowing people who could not afford to attend the conference in person to still participate in many meaningful activities related to the conference itself.

It would definitely require more work from participants than is typically expected for a conference, and I’m sure this would turn some people away from attending this conference. That being said, those people I think rarely get very much out of typical conferences anyway, and I’d rather not build a new conference model based on the lowest common denominator.

Do you see any flaws with this model? Can you think of any ways of improving it?

March 20, 2012 / 4 Comments

Math in the real world: Gardening

My uncle called me today, and asked me a math question. Normally, I get called and asked technology related questions, but occasionally people remember that I have a mathematics background and call me in to assist.

My aunt wants to build a raised garden bed with a very particular shape. My uncle has been tasked with building it. She wants 3 of the sides of the shape to be 4 feet long, and the 4th side to be three feet long, and the whole shape should form a trapezoid (with a line of symmetry down the middle of the trapezoid). It took a little bit of chatting on the phone to get this to be clear, and I can see how being able to send each other pictures would have been really useful. To be able to build this shape as accurately as he would like, he needs to know all of the angles of the shape, so he can cut the pieces of the wood with the angles in the right position using a miter saw.

Trapezoid garden bed

I looked at the shape and decided that the fastest solution would be to build the shape in Geogebra, and measure the angles, which resulted in this.

Not the exact solution, but close enough that my uncle would be able to use the miter saw (which has a maximum accuracy of 1 degree, according to my uncle) and cut the wood for his shape. It took me about 3 or 4 minutes to draw the shape in Geogebra and measure the angles.

After my phone call with my uncle was over, I decided that I should double check this solution though, and verify that I knew how to solve it.

I drew an imaginary line across the shape, and labelled that side x. This allowed me to create a pair of equations using the Cosine law, and I ended up with the following equation to solve:

First equation

which simplifies to:

Second equation

and finally leads to this calculation:

Third equation

On my calculator, that leads to a value of the smaller angle of about 82.8° and a larger angle of 97.2°, which means that my diagram that I drew for my uncle is fairly close. Wanting to be sure that my answer was correct, I also checked it using Wolfram Alpha, and on my graphing calculator.

After I told my uncle the solution, he told me that my aunt had suggested drawing the diagram carefully on a piece of paper and measuring the angles with a protractor, but he had complained that solution wasn’t "mathematical enough." Of course, this leads to a discussion of what it means to do mathematics, anyway.

Does it matter which way I solve this problem for my uncle? Which of these techniques would you classify as "mathematics"? All of them? None of them?

March 20, 2012 / 9 Comments

We need social media etiquette

We need to develop social media etiquette. Some of the conversations I have seen on Twitter have been out of control rhetoric, other tweets have just contributed to the noise, and benefitted no one. During our discussion on how to make Twitter more accessible to new people, I tweeted some "rules" that if all followed, Twitter would be a lot more accessible and usable for everyone.

Of course, these rules are just my interpretation of what should be useful, and probably need to be reworked. Also, the idea for this comes from the email charter, which I strongly recommend you make an effort to implement for yourself.

The network is capable of only so much information. Don’t overload the network.
Be kind to each other, and assume that tweet did not convey the message intended.
Links are a way of sharing extra information in a conversation. Use them sparingly.
When you see a question asked, answer it, even if your answer is to redirect the questioner to another source of information.
The purpose of the social media is not to gain influence, it’s to communicate ideas. Don’t forget the social in social media!
Where reasonable, give attribution to ideas that you find & your sources of information.
Take some time to think about what you are tweeting. Is this contributing to the conversation?
It’s okay to disagree with someone, but do it respectfully. Don’t tweet what you wouldn’t say to someone’s face.
Be safe. Stop before you click on a link & think, does this link have a context which makes sense?
Stop making lists of the "best people" to follow on Twitter. This is completely subjective & exclusionary.

There are other "rules of Twitter etiquette" out there. Here is a page for Twitter etiquette that @jlubinsky found and here’s another article on Twitter etiquette shared by @PivotLearning. There are also other useful resources on social media etiquette here, here, and here, as shared by @erringreg

How would you edit this list? Is it necessary?

March 18, 2012 / 3 Comments

Intuition and research

There are a number of things which have been discovered over the years through research which are not entirely intuitive. In fact, many of the results that have been discovered are down-right odd.

If you pay people to perform simple, routine tasks, in general the more you pay the person, the better they perform. Oddly enough, if those tasks require even a bit of cognitive effort, extra pay reduces performance. What!? How does this apply to education? Well, first it seems that it would drive a nail into the coffin that we should give teachers merit pay (as opposed to just paying all teachers more) for improved student performance. It also suggests that other rewards, which are commonly used in education, may have the opposite of the intended effect; they may reduce performance.
If you tell children how to play with a toy, they are less likely to perform irrelevant actions with that toy; but they are also less likely to do anything novel with it, or discover anything beyond what you told them about the toy. One would think that if one knew how to use a toy effectively, you’d have a base of knowledge necessary to expand upon and to make new discoveries. It turns out; sometimes even a little bit of knowledge is too much.
In a pivotal study done in the 1980s, researcher Jean Lave sought to find out how successfully people applied math in their everyday lives. Her surprising answer is that people actually use mathematics reasonably reliably, at nearly 98% accuracy in the supermarket, for example. What is somewhat shocking is that when the very same people were given a pencil and paper test on the very same skills they had successfully solved in the supermarket, the percentage they got right dropped to 59%. The conclusion Jean Lave had was that the subjects were using strategies in the supermarket that they had developed themselves, but fell back into the strategies they had learned in school for the test.
What do you think would happen if you didn’t teach arithmetic at all to students? In a highly unethical study done in the 1930s, a group of students was given no arithmetic instruction at all until 6th grade. Instead, the students spent this time discussing things that came up in their lives, and some practice in measuring and counting. In 6th grade, the students were taught arithmetic. At the end of the 6th grade, this group of students (who came from the poorest parts of the district) exceeded their peers from the other schools in solving story problems, and had caught up in arithmetic. In other words, not teaching math for 5 years (and spending this time reasoning through discussion instead) improved their mathematical reasoning skills.
A longer work week does not necessarily lead to more productive employees. In fact, most often it reduces overall employee productivity. 40 hours a week seems about optimal (for maximizing productivity, if not morale). What are the implications of this research on education? Should we be looking at less time in school (or at least doing "work" like activities for students) rather than more?

What these studies show is that our intuitive sense of what may be true is often not true, or at least can be shown to be not true under certain circumstances. We must then shy away from relying entirely on our intution, especially when examining large-scale educational practices. We must do a better job in education in funding and supporting effective research in our schools. We also need to be less reactionary when it comes to approaches that don’t fit into our personal perspective on how certain things should be taught, and focus more on dialogue and research to satisfy our reactions.

March 16, 2012 / 8 Comments

Rethinking the standard school schedule

Race to Nowhere

I just read an interesting article on the Salon about how long work weeks produce lower quality work, and that it seems that about 40 hours a week is when the maximum productivity occurs. Of course if this applies to workers, then it presumably (or a similar number) applies to students as well.

So an obvious question is, how many hours are students in school?

In our school, students start school at 8:30am and are at school until 3:30pm with an hour for lunch. This means that they "work" about 6 hours each day*. If they have 2 hours of other "work" to do each day, then they would be working a productive 40 hour work. If they are working more than this, then their productivity drops and one would expect reduced gains for additional time worked, and tremendous drops in productivity after a few weeks of increased work load. What is often forgotten in these types of calculations though is all of the other work students do outside of school.

When students spend time doing adult-type work, like an after school job, or they participate in after school sports, or tutoring, or another school, they are adding onto the total amount of work they have done in a week. The most important work that they do, of course, is learning. This analogy between the 40 hour work week, and how many hours students "work’ at learning has an important caveat; 40 hours may be way too much "work" for students, especially younger ones.

You may notice at your own school that students productivity drops after a few weeks in school. In fact, I can remember this effect quite clearly as we talk about it nearly every year. According to the article, people can sustain slightly greater amount of effort for small periods of time, but each week of extended effort has an additional toll on productivity. So by this logic, the drop-off in student output that educators frequently notice may be due to the over-extension students have been through during the previous weeks.

A potential solution, proposed by a colleague of mine, is to take the month of August (or July) and expect students to come to school during this month, for 4 days a week. This would produce 16 – 18 additional days per year of school, which could be used to offset 16 – 18 long weekends during the rest of the school year. Students would have the same amount of over all time spent in school, but it would be more balanced through-out the year.

There is some support from parents for a change like this in education. The parents behind Race to Nowhere know about this issue intimately. They have been pushing for a shorter week for students for ages. Further, by reducing the length of the summer, students who do not participate in learning activities in the summer would be less likely to experience the ‘summer-time drop.’ Unfortunately, students who normally spend their summers doing highly engaging learning activities would lose some of this time. On the other hand, they would gain many more long weekends during which they could choose to enrich and extend themselves.

There are some organizations which are calling for an extended school day. Kipp Schools are a famous example of a school system where students spend much more time in school. The attempts from these organizations to extend the school day are misguided, at least if you believe the research on productivity versus hours worked. There is some research showing that the increased school year and increased school days at KIPP schools improve student results, but that research has been recently contested because KIPP schools tend to be more selective in their enrollment than the neighbouring schools.

We have to be careful to keep separate ‘seat time’ from productive learning time. Students who are more alert, more productive, and more engaged in what they are doing will learn more. Simply being in school longer, or working longer at school work, will not ensure that students learn more. We need to remember that the same principles that apply to our own well-being apply to students as well. There are philosophical reasons to be opposed to excessive amounts of work for students, it seems that there may also be some research to support these claims.

March 14, 2012 / 5 Comments

Copyright for Canadian Educators

I’ve created a brief presentation on copyright which simplifies (perhaps too much?) copyright for teachers. Please give me some feedback on this presentation before I use it with my colleagues. Note: These tips on copyright only apply to Canadian educators as copyright rules are specific to each country. For example, Canada has no "fair use" provision.

Update: This presentation needs to be updated with the recent changes to Canadian Copyright law. See Copyright Matters! for more accurate information.

March 13, 2012 / 0 Comments

Articles I’ve written on Math Education

Here is a list of some of the articles I’ve written on Math Education

On Mathematics education reform:

On the use of technology in mathematics education:

How does technology affect us?

I’m presenting this morning to our 5th grade students on technology. My objective is to get them thinking about how we define technology, and how in some cases, technology defines us.

M	T	W	T	F	S	S
			1	2	3	4
5	6	7	8	9	10	11
12	13	14	15	16	17	18
19	20	21	22	23	24	25
26	27	28	29	30	31