I’m always on the look-out for ways of finding connections between mathematics and other areas of knowledge. Music is one of the areas of knowledge that I know has some similarities with mathematics, and so I’ve been brainstorming ways one could incorporate music into a mathematics classroom. Here are a few examples.
- A musical scale is an example of a sequence (of notes) and could be used to show the idea the order of objects, related to the order of numbers. As each note in an ascending scale is played in sequence, students should be able to hear that the notes have a order, and then you can relate this order to the order we associate with the counting numbers.
- Introducing students to patterns can also be done nicely with music, either with notes, or with percussion instruments. Here are two sample patterns. One simple activity to do with students here is to have them produce their own different types of patterns.
- You can also use music to develop some conceptual understanding of skip counting. Often children are taught to count by 2s and 3s but do not necessarily understand what this means. Obviously one should use manipulatives and other techniques to develop this understanding, but here’s an example of how skip counting sounds in music. This example could also be used as an introduction to simple linear functions as well at a later grade.
- You could introduce students to fractions by comparing relative sizes of different notes. In the example below, the music starts off with 16th notes, followed by 8th notes, quarter notes, half notes, and finally a whole note. Can you hear how obvious the difference is between the notes?
- Music notes themselves are sound waves, which if you have an oscilloscope, you can visualize directly as you listen to a note. A pure note has a relatively simple associated wave, but notes as played on a music instrument are almost always composed of multiple harmonics (or waves of different frequences added together). This is an example of a capture from a digital oscilloscope. What do you think the seemingly random waves that appear between the notes are from?
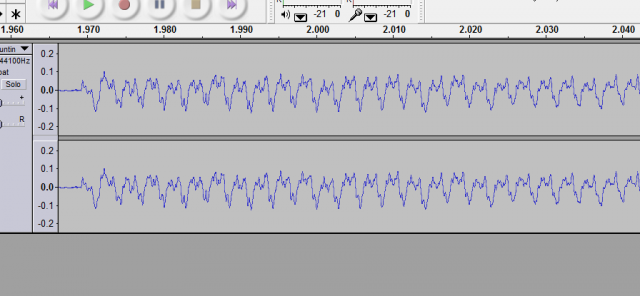
You can also visualize the volume of the notes (by opening up an audio recording of some music being played in a program like Audacity, for example), and notice an interesting drop-off that occurs. If you measure this drop-off closely, it should match an exponential decay function.
Notice also what the volume of the notes over time looks like when we zoom in on one of them.
- Imagine you played one note on the piano at one constant speed, and another note at a different constant speed. After how many notes would you play both notes at the same time? This is an application of the lowest common multiple (provided you express the number of notes played per unit time in lowest terms). Below is a video where one note is being played at a rate of 120 times per minute, and in a different recording, the same note is being played at a rate of 150 times per minute. Do you notice something interesting when both recordings are played simultaneously?
- Another area where mathematics comes into play is in the ratio of the wavelengths of different notes. Karen Cheng does an excellent job of explaining how this relates to why we appreciate some music more than other music.
Hopefully these short examples give you some examples of how mathematics and music are related. In another post, I intend to look at musical instruments, and how mathematics can be used to construct them.
* Musical scores created with Noteflight. This program has a free demo one can use without signing in, but if you want to save your work, you will need to sign up for a free account.
** If you are viewing this post in your email, none of the videos will be visible, so I recommend reading it online here.