An instructional routine is a consistent way of interacting with learners. The primary benefits of a routine emerge when the teacher and the learners know the routine well enough that the steps fade into the background, and everyone can focus more on the ideas being shared.

All successful teachers use instructional routines, but not all routines are equally effective. Below are some routines that educators have tested, and all have one important trait in common—they treat learners as sense-makers.
Choral Counting
In this routine, students look for structure in numbers that emerge as they count those numbers as a whole group. First, given a starting number and an amount to count by, the class counts together as an entire group, then the teacher pauses the class to give students opportunities to look for structure. Students then share some of the patterns and relationships they noticed.

More detail on this routine is available here: https://tedd.org/choral-counting/
Connecting Representations
This routine, developed by Amy Lucenta and Grace Kelemanik, asks students to use mathematical structure to connect two visualizations of the same mathematical idea represented differently.
After this activity is launched, students are presented with two different kinds of representations. They then make matches between one type of representation and the other. Once they have matched made with their partner, the teacher orchestrates a classroom discussion where students describe how they made their matches. Typically, a representation goes unmatched, so students create the missing representation next. Finally, students reflect on what helped them make their matches — what might be helpful to pay attention to next time.
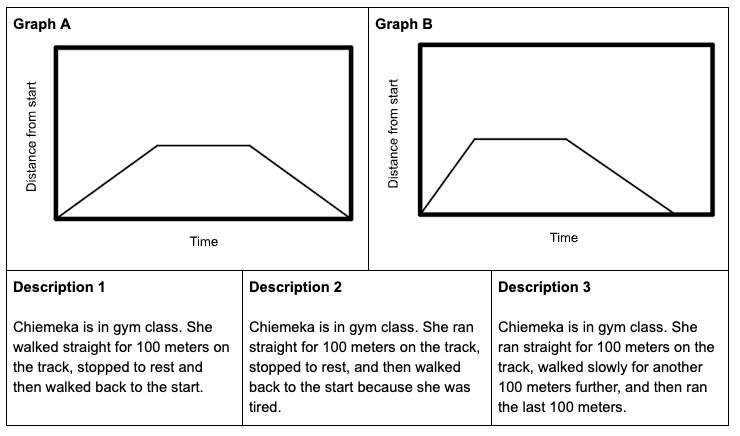
More information on this routine is available here: https://www.fosteringmathpractices.com/connecting-representations/
Contemplate then Calculate
This routine, also developed by Amy Lucenta and Grace Kelemanik, asks students to use mathematical structure to create shortcuts for calculations.
After this activity is launched, students are given a glance at a mathematical image. They are asked to share what they notice while their teacher records these noticings for everyone. Students are then given the mathematical image again, this time the remainder of the class, along with a question to address related to the image.

More information on this routine is available here: https://www.fosteringmathpractices.com/contemplate-then-calculate/
Counting Collections
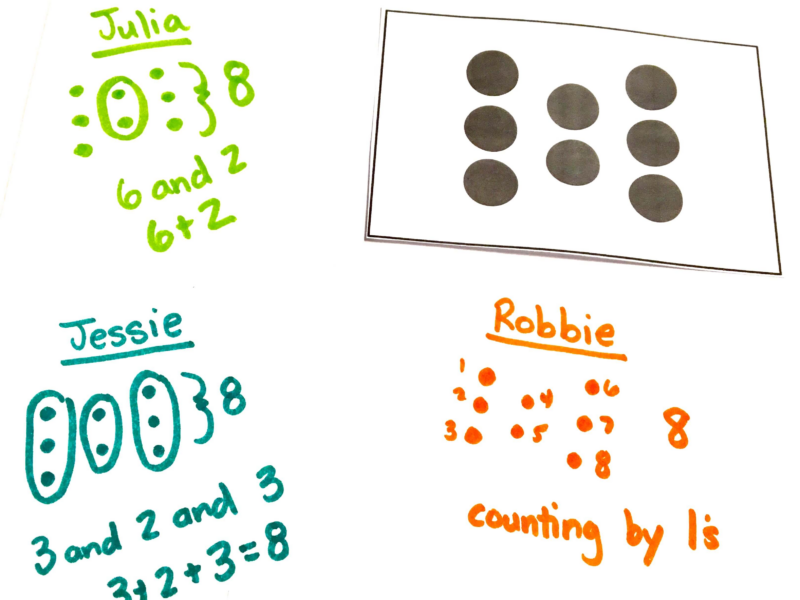
Angela Chan, Megan L Franke, and Elham Kazemi describe this routine in detail in their book Choral Counting & Counting Collections. In it, students count objects and then represent how they count them.

The magic of this routine is in the time spent by educators watching students count and keeping track of students’ ability to use one-to-one correspondence, mathematical structure, place value, skip counting, etc… as they count.
More information on this routine is available here: https://tedd.org/counting-collections/
Number Talks
The goal of a number talk is usually to expose students to multiple strategies for solving the same mathematical problem. Students are given a mathematical problem to solve, usually a problem involving arithmetic or counting, and asked to come up with a solution in their heads. Once sufficient numbers of students have indicated that they have a solution, the teacher leads a discussion where several solutions are shared.
This routine is terrific for celebrating learning that has occurred but doesn’t necessarily press students into using new strategies. For that, one wants to use a problem string instead (see below).
There’s lots of great information on number talks on this page: https://brownbagteacher.com/number-talks-how-and-why/
Problem Strings
A problem string is a deliberately selected sequence of problems given to students, one at a time, to help students develop a new mathematical strategy. They are similar in how they are run to number talks but are not necessarily restricted to arithmetic or counting problems. Problem strings lend themselves well to all areas of mathematics.

Pam Harris has some resources for problem strings on her website here. She’s also written a terrific book on problem strings in high school. There are resources here on implementing a specific kind of problem string called a number string here: https://tedd.org/number-strings/
Three Reads
Three Reads is a routine used to help students make sense of contextual problems and learn how to deconstruct mathematical problems they have read. First, the routine is launched with an explanation of what students will work on, why they are working on it, and how they will work on it. Next, students read the same mathematical problem three times, each time for different types of information. Finally, they share what they understood from their reading with each other. Over time, students get better at mathematical reading.
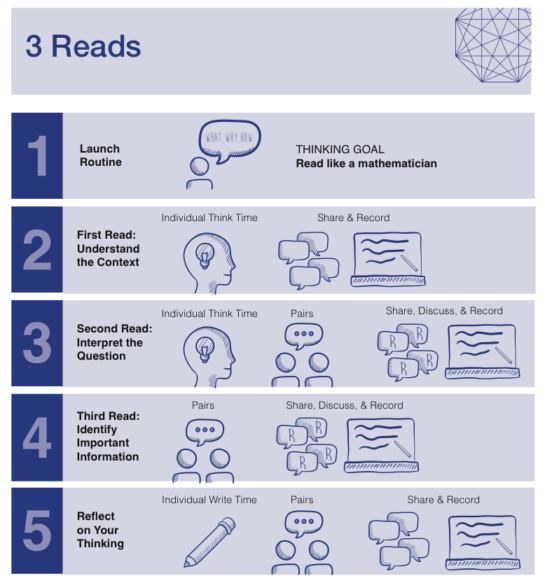
Amy and Grace wrote a chapter on this routine in their book Routines for Reasoning, and I highly recommend reading their book to learn more about it.
Which One Doesn’t Belong?
The goal of this routine is to spark mathematical creativity, give students opportunities to construct mathematical arguments and show them that there are many mathematical questions one can ask that do not have a single correct answer. The most important part of this routine is the argumentation students develop as they justify their choice.
Students are given four different mathematical objects in a collection and asked to explain which one doesn’t belong. Usually, students do this first on their own, share their ideas with a partner, and then their teacher leads a mathematical discussion based on their ideas.

For more information on this routine, visit this website or read Christopher Danielson’s wonderful book on the routine.
Examples – Non-Examples
In this routine, students are presented with examples and non-examples. They analyze each pair and come to a better understanding of the concept presented by the examples.
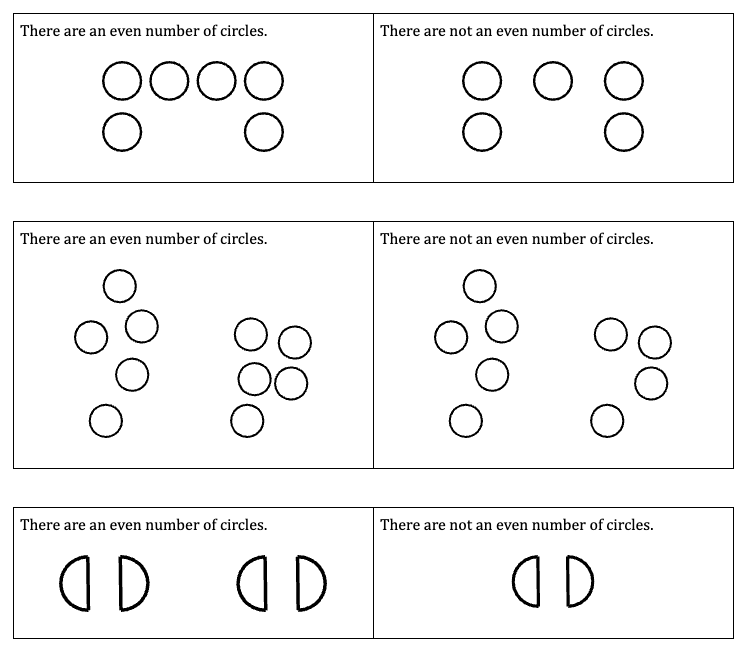
Using examples and non-examples is perfect when you have a mathematical concept for which you want students to have a definition. This is especially helpful as students often struggle to understand definitions given to them without sufficient explanation.
A guide for getting started with this routine is available here.
Sharing Skepticism
The Sharing Skepticism routine is intended to support students in constructing arguments, critiquing each other’s arguments, and reflecting on what makes an argument good. Over time, as students debate which arguments are more convincing, they will develop the habits of mind necessary to construct mathematical arguments. The overall structure of the routine is for students to convince themselves, convince a friend, and then convince a skeptic.
First, the routine is launched so that students know why they are sharing skepticism today, what they will learn, and how the routine proceeds. Next, students solve a problem independently and then share their solution with a partner. Two or three solutions are presented to the whole class; then, students work with a partner to select their favourite argument and try to improve it somehow. Some ideas for improvement are shared with the class, and then students reflect on their experience and consider what makes a good argument.
Any task that every student can devise a strategy for solving, which requires some level of mathematical thinking and has multiple strategies for solving, can be used as a task for this routine.
More information on this routine is available here.
Paired Examples
This routine aims to help students make connections between different mathematical concepts, allowing them to explicitly build a procedure or algorithm from something they already know.
First, the routine is launched, and then students are presented with the first step in each pair of mathematical procedures. Students look for and name connections between each step. Each step is unveiled in the same way, with students sharing the connections they notice in a structured way with the whole class. Once the entire procedure is unveiled, students are presented with another example of the new procedure for them to try, first independently and then working with a partner. A couple of these new procedures are selected to be shared with the whole class. Finally, students reflect on what they learned from the activity.

This routine is ideal anytime there is a mathematical procedure one wants students to learn when there is an early similar mathematical procedure students have already learned. The earlier example does not need to be identical to the new procedure. Students noticing the differences between the two can be as powerful as noticing the similarities.
Further resources related to this routine are available here.
Language Routines
There are times when the focus of a mathematics classroom is on building language, both the academic language of the discipline of mathematics and the everyday language needed to converse about mathematical ideas with each other.
The eight language routines developed by the Standard Center for Assessment, Learning, and Equity are ideal for these moments.
- MLR 1: Stronger and Clearer Each Time
- MLR 2: Collect and Display
- MLR 3: Critique, Correct, and Clarify
- MLR 4: Information Gap
- MLR 5: Co-Craft Questions and Problems
- MLR 6: Three Reads
- MLR 7: Compare and Connect
- MLR 8: Discussion Supports
Each routine is described in a little detail in the teacher guide for the Illustrative Mathematics curriculum. The IM curriculum also contains many examples of when and why one might want to use the math language routines.
Group Learning Routines
For those teachers who teach multiple subjects, the subject-agnostic group learning routines developed by All Ed may be ideal. Each routine is described in detail, and different routines are provided for different use cases.
One of my favourite group learning routines is Idea Carousel, and I frequently use it in professional development sessions. In this routine, learners have a big idea they are unpacking, and the components of this big idea have been separated into separate posters. Learners are given one marker for each group and rotate through the posters around the room, swapping the marker to another recorder on each rotation. As learners circulate, they add detail and annotate the previous ideas added by other groups. At the end of the carousel, the teacher leads a whole group conversation based on the posters.

Routines for Teacher Learning
While all of the routines I’ve described before lead to educator learning, there are specific routines designed for people who facilitate teacher learning to use.

Susan Jones says:
** So much ** information 😉 I’d need to remind myself that to become a routine, it has to happen enough to be familiar, so I’d do better picking one or two for starters, and to play around with when to focus on concrete or visual or abstract….
March 16, 2024 — 1:32 pm
Blue says:
I love the figure at the top of the article showing the shift in cognitive load.
April 10, 2024 — 9:31 am