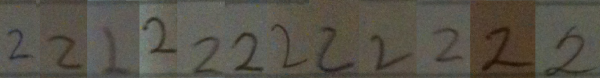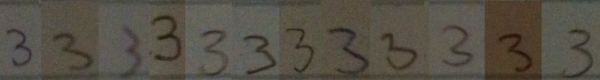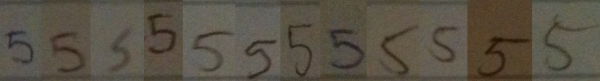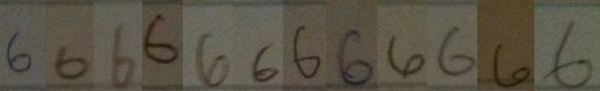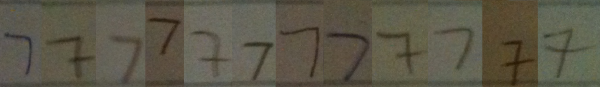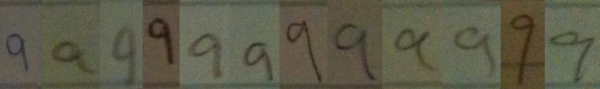Education ∪ Math ∪ Technology
I’ve updated my presentation on social media, aimed at a parent audience (although I’m sure it could be used with educators just as easily). Embedded below. Note: The first few slides, up to slide 39, are intended to be shared fairly rapidly, to create a sense of overload in the viewer.
(Viewing this in your email or RSS reader? Try this link instead.)
In the not too distant future, there will no educational technologists. That is, there will eventually be no people who specialize primarily in teaching other people how to use technology. The reason why we have educational technologists now is that the rate of change of technology is so high that many people struggle to keep up with the changes, and so some of us have specialized in "keeping up with changes in technology."
The positions that will exist will be analogous to the role of librarians in schools, who do not primarily teach people how to operate books, they teach them how to read and utilize books (and other forms of text material) to learn about the world. In fact, it seems quite likely to me that librarians in the future will include at least a minor role in teaching others how to research using technology, and how to use and critically examine technology as a learning tool, in much the same way that many librarians do already.
Moore’s law, which famously states that the number of transistors on integrated circuits doubles every two years, may be more appropriately modelled with logistic growth rather than exponential growth. Logistic growth behaves very much like exponential growth initially, but as finite limits in resources or capacity are reached, growth slows down, and eventually levels off. It is very likely that instead of run-away technological growth and a singularity, that we will eventually reach a point where our hardware capabilities will remain somewhat stable, and when this happens, eventually software will follow suit. A strong benefit of software equilibrium is that bugs in code will be less frequent, and interoperability between different software will be easier to maintain, leading to technology which is much more reliable overall.
What this means is that the rate of change of technology will eventually slow, and people will have to devote less of their time to keep up with the changes, which means that being specialized in "keeping up with the changes" like educational technology people do, will be less of an advantage over others.
Another possibility is that technological change will not slow down, and that eventually there will just be people who have merged with the technology, and people who have chosen not to. In this case, educational technologists will be equally unimportant as the people who do not merge will be completely left behind by technology, and the others will not need our support. This kind of scenario is fairly dystopian from my point of view, so I prefer the first alternative.
A third possibility is that our ecosystem crashes completely, and our civilization follows soon after. In this case, we will not need educational technologists because we will be spending most of our time just trying to survive. Again, the first scenario for me is far preferable!
Given that equilibrium in software is likely to happen long after hardware equilibrium, our roles are probably safe for at least a couple of generations.
I’m working on a couple of short videos comparing the standard algorithm for a multiplication and addition, and considering some ways of using other algorithms which are more likely to make sense for students.
To be clear, these presentations do not enough justice to student-created algorithms, which I would strongly recommend as a starting place for exploration of algorithmic reasoning. These two videos are merely an attempt to compare two different algorithms against each other, and to provide some support for teachers interested in learning more about why we might want to use something other than the standard algorithms in our classrooms.
I also want to make it clear that how I am describing these distinctions in the videos is not how I would introduce them to children (or adults for that matter, if I have the time). Instead, I would start with setting up realistic situations, whole group, and small group discussions around investigating these operations, using both manipulatives and symbols to represent numbers in the algorithms. A really useful activity, for example, is for children to be making these comparisons themselves, so that they can look for patterns in different operations, and abstract these patterns into general rules they can follow to make their use of any algorithm easier.
I see these algorithms as a useful way to get started with abstract reasoning, provided they are framed in a certain way, as described below.
Multiplication
Addition:
Dave Cormier, in an excellent, excellent presentation, made the point that learning multiplication tables belongs to the "simple" domain of knowledge (which in his defense was probably an example he chose to help his audience understand the Cynefin framework). I think I need to understand his definition of simple better, because I do not see multiplication, especially when it is typically learned, as particularly simple.
I’m not trying to pick on Dave in particular, I have heard "multiplication is simple" from a lot of different sources, Dave’s presentation is just the most recent place. Look at the Cynefin framework below to get a sense of how Dave is classifying areas of knowledge.
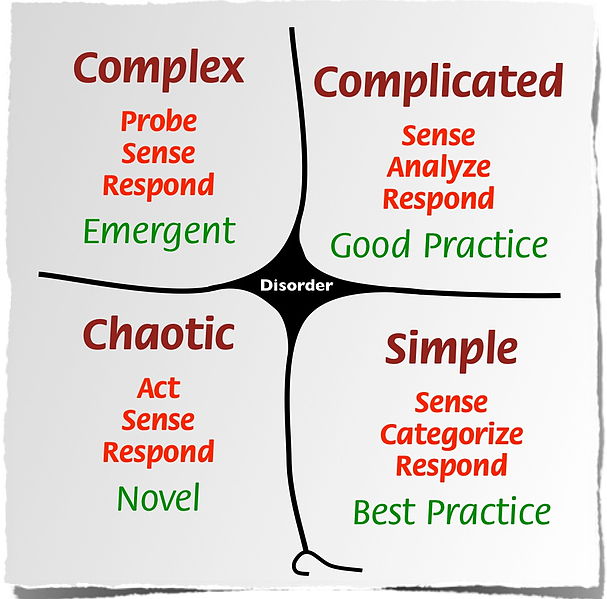
(Image credit: Dave Cormier)
I’m going to argue that multiplication as an area of knowledge more appropriately belongs to the complicated domain (especially for children).
First, the symbols used for multiplication (numbers) are a complex idea, and it is not entirely clear to me that every child really understands the relationship between numerals and numbers by the time they are introduced to multiplication. Numerals are a more complex topic than I think most people realize.
Here is some data to support this claim.
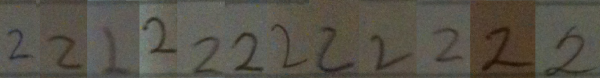
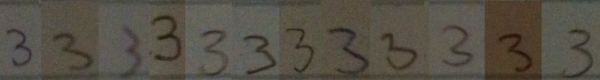
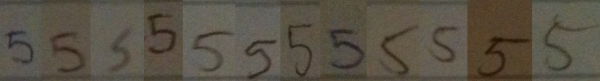
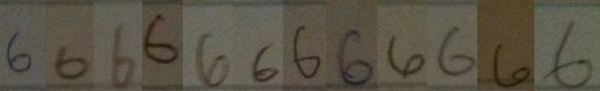
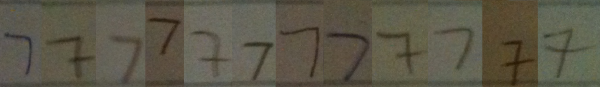
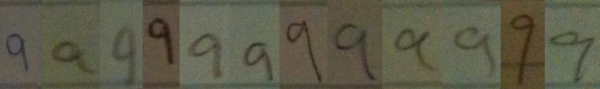
I went around my school and found 12 people (6 grade 11 students and 6 adults) to volunteer to write down the numbers from 1 to 10 in a row on a blank sticky note. I then took photographs of the sticky notes, and reorganized the numerals so that they were grouped by numeral type, rather than by person. It should hopefully be clear from these samples that when we teach students how to recognize numerals, we are really teaching them to recognize a class of objects which have similarities, but that there is no single way to write any numeral.
The idea of numbers themselves is complex. Different cultures may have different internal models for numbers, with some cultures being reported not to have an internal linear sense of numbers. It may even be that our sense of numbers doesn’t just vary at a cultural level, but at finer grain structures than entire cultures. Your sense of what numbers are is likely influenced by your parents, your local cultural, and our global cultural representations of numbers.
Multiplication itself exists in a culture, with different cultures viewing multiplication differently. There is currently no wide-spread agreement on whether multiplication is best represented with arrays, as repeated sums, as an area model, or as an algorithm used to calculate in these contexts. Given that mathematics educators do not all agree on something as fundamental to multiplication as how we define it, it hardly seems reasonable to call it simple.
Further, there are a large number of different algorithms for multiplying numbers, and many different possible representations. Some of these algorithms focus on mental arithmetic, others on visual representations, and others on numerical calculations. There are benefits and drawbacks to each of these methods, leading me to conclude that there is no, one best way to multiply numbers.
To top it all off, students, not all of whom even know how to tie their shoes, are expected to start mastering this skill and idea at age 8. I think that the idea of "simple" is a relative term. What might be simple for an adult might well be incredibly complicated for a child.
At our school we currently have open-access to the printer by our students. Unfortunately our students waste a lot of paper, usually reprinting something 10 times without checking to see if the printer is actually working and/or has enough paper. We work with students to try and improve their use of the printer, but in the mean-time, we have a lot of paper which has already been printed on one side, and which would otherwise go to waste.
Here are some ideas on what schools could potentially do with all of that paper.
Paper folding has strong links to mathematics and art. It could provide a context for a mathematical activity so that students see the mathematics they are learning applies to parts of the world, rather than being just symbols on paper. Students can also use paper folding as a way of expressing themselves through art.
(Image credit: josey4268)
Any other suggestions?
I’ve started a presentation on grading, which anyone with the link can edit and add their perspective. The presentation is split into four areas:
Please feel free to add your perspective to this summary of the debate on grading, ideally citing evidence for any strong claims that you make if possible.
https://docs.google.com/presentation/d/1tu3y6DU5IrT-Y68tva_mZHM7HYeGvpZMfRBMdxY3x38/edit?usp=sharing
Remember that there are a lot of emotions behind the different perspectives on this issue, so to refrain from personal attacks, etc… My objective is to gather evidence and perspectives, rather than start any flame wars.
My mother has offered to give us a small amount of money, which we can either use to pay down most of our debt, or we can put into a savings account, and then pay down the debt over time.
My wife and I have been debating which is the better course of action. After playing around in Excel, I decided to write a script to help us resolve this issue. See https://davidwees.com/javascript/debtsavings/.
I also gave this problem (with the actual numbers my wife and I are looking at) to my 12th grade students as part of our review for their IB exams in May. One student’s reaction, "This is a real problem? Really? Wow."
*Disclaimer: The script in question is a work in progress, it may contain bugs, and should not be relied upon to do any actual financial planning.
Which of these ways dominates? Why?
* Note: There are some tasks which overlap. Programming a computer (under the creation category) to achieve a specific task could be a form of assessment, for example. Also, one could probably argue that "exploration" and "programming" aren’t really distinct categories.
"Just as we know students don’t learn simply because we tell them something, teachers don’t learn simply because we hand them a journal article." ~ Jo Boaler
This is part of my daily challenge as a learning specialist for mathematics and information technology. I can share research, suggestions, and resources, but how much of what I share actually changes practice?
Here is what I have found that does make a difference in their learning for my colleagues:
Here’s what I do not do:
Grant Wiggins shared an article on his blog called "The Nature of Proof." The article describes a course in geometry given in the 1930s that was not only extremely influential for those who took the course, many of them described it as the most important course they ever took in their entire lives. Here’s a quote from the teacher of that course.
"While teachers of mathematics say they want the young people in our secondary schools to understand the nature of proof, that should not be and probably is not their total concern. What these teachers really want is not only that these young people should understand the nature of proof but that their way of life should show that they understand it. Of what value is it for a pupil to understand thoroughly what a proof means if it does not clarify his thinking and make him more "critical of new ideas presented"? [emphasis mine] The real value of this sort of training to any pupils id determined by it effect on his behavior and for purposes of this study we shall assume that if he clearly understands these aspects of the nature of proof his behavior will be marked by the following characteristics:
- He will select the significant words and phrases in any statement that is important to him and ask that they be carefully defined.
- He will require evidence in support of any conclusion he is pressed to accept.
- He will analyze the evidence and distinguish fact from assumption.
- He will recognize stated and unstated assumptions essential to the conclusion.
- He will evaluate these assumptions, accepting some and rejecting others.
- He will evaluate the argument, accepting or rejecting the conclusion.
- He will constantly re-examine the assumptions which are behind his beliefs and which guide his actions."
Harold Fawcett, The Nature of Proof, Page 11, 1938
The use of "He" in this quote should be understood in the context of when this quote was written, and could easily be substituted for "The student" or something similar.