Dave Cormier, in an excellent, excellent presentation, made the point that learning multiplication tables belongs to the "simple" domain of knowledge (which in his defense was probably an example he chose to help his audience understand the Cynefin framework). I think I need to understand his definition of simple better, because I do not see multiplication, especially when it is typically learned, as particularly simple.
I’m not trying to pick on Dave in particular, I have heard "multiplication is simple" from a lot of different sources, Dave’s presentation is just the most recent place. Look at the Cynefin framework below to get a sense of how Dave is classifying areas of knowledge.
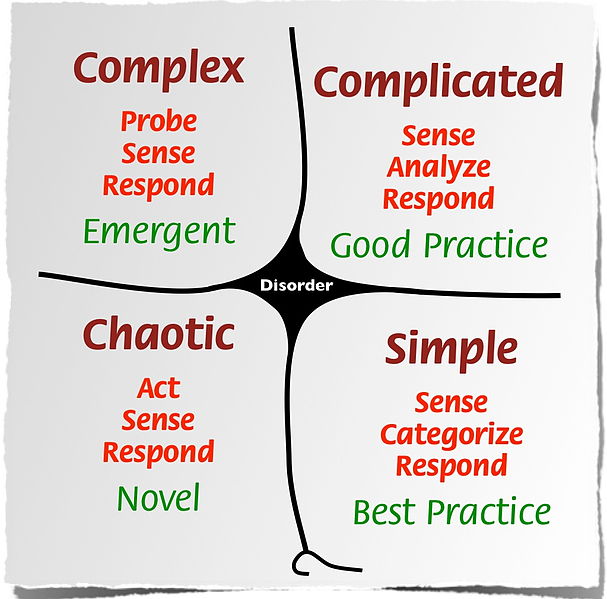
(Image credit: Dave Cormier)
I’m going to argue that multiplication as an area of knowledge more appropriately belongs to the complicated domain (especially for children).
First, the symbols used for multiplication (numbers) are a complex idea, and it is not entirely clear to me that every child really understands the relationship between numerals and numbers by the time they are introduced to multiplication. Numerals are a more complex topic than I think most people realize.
Here is some data to support this claim.

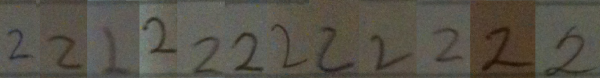
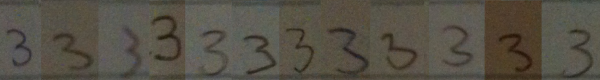


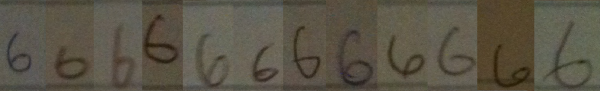
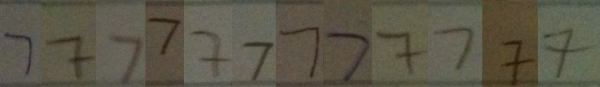

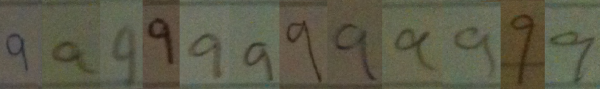
I went around my school and found 12 people (6 grade 11 students and 6 adults) to volunteer to write down the numbers from 1 to 10 in a row on a blank sticky note. I then took photographs of the sticky notes, and reorganized the numerals so that they were grouped by numeral type, rather than by person. It should hopefully be clear from these samples that when we teach students how to recognize numerals, we are really teaching them to recognize a class of objects which have similarities, but that there is no single way to write any numeral.
The idea of numbers themselves is complex. Different cultures may have different internal models for numbers, with some cultures being reported not to have an internal linear sense of numbers. It may even be that our sense of numbers doesn’t just vary at a cultural level, but at finer grain structures than entire cultures. Your sense of what numbers are is likely influenced by your parents, your local cultural, and our global cultural representations of numbers.
Multiplication itself exists in a culture, with different cultures viewing multiplication differently. There is currently no wide-spread agreement on whether multiplication is best represented with arrays, as repeated sums, as an area model, or as an algorithm used to calculate in these contexts. Given that mathematics educators do not all agree on something as fundamental to multiplication as how we define it, it hardly seems reasonable to call it simple.
Further, there are a large number of different algorithms for multiplying numbers, and many different possible representations. Some of these algorithms focus on mental arithmetic, others on visual representations, and others on numerical calculations. There are benefits and drawbacks to each of these methods, leading me to conclude that there is no, one best way to multiply numbers.
To top it all off, students, not all of whom even know how to tie their shoes, are expected to start mastering this skill and idea at age 8. I think that the idea of "simple" is a relative term. What might be simple for an adult might well be incredibly complicated for a child.
Robert Chester says:
Your examples are tough to be done. Yes, Numerals are a more complex topic than I think most people realize
best australian online casino
May 22, 2013 — 3:39 pm