(Source: Engaging ALL students in Cognitively Demanding Mathematical Work, November 4th, 2014)
On Tuesday, November 4th we had Grace Kelemanik do a presentation and a workshop for the teachers in our project intended to offer ways to use the standards for mathematical practice to support English-language learners (ELL) and students with special needs.
Introducing the ideas
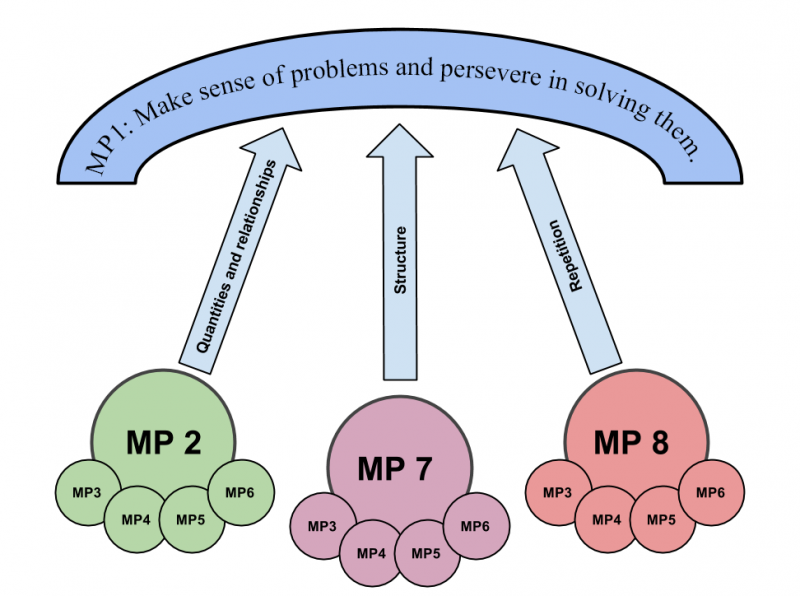
As the picture above suggests, Grace does not consider all the mathematical practices from the Common Core as being equal in importance. In particular, she sees MP2 (Reason abstractly and quantitatively), MP7 (Look for and make use of structure), and MP8 (Look for and express regularity in repeated reasoning) as being potential pathways students can use to solve mathematical problems.
If you want to support students in using MP2 to solve problems, consider the following questions:
- What can I count or measure in this problem situation?
- How do the quantities relate to each other?
- How can I represent this problem?
- What does this (expression, variable, number, shaded region, etc.) represent in the problem context?
If you want to support students in using MP7 to solve problems, consider the following questions:
- What type of problem is this?
- How is this (situation, object, process, etc.) connect to another math idea?
- Is it behaving like something else I know?
- How can I use properties to uncover structure?
- How can I change the form of this (number, expression, shape) to surface the underlying structure?
- Are there “chunks”?
If you want to support students in using MP8 to solve problems, consider the following questions:
- Am I doing the same thing over and over again?
- Am I counting in the same way each time?
- Do I keep doing the same set of calculations?
- What about the process is repeating?
- How can I generalize this repetition?
- Have I included every step?
These questions come directly from Grace’s presentation and are likely to be included (along with more examples) in a book Grace and her co-authors (Amy Lucenta and Susan Creighton) hope to complete soon. The questions remind me of the general problem solving heuristics that George Polya developed, but with a greater level of specificity, perhaps one that students can generalize to any problem context themselves.
Modelling the practices
In the afternoon, Grace modelled some of the practices she talked about in the morning and in particular focued on how a lesson focused on using MP7 could help students make sense of the mathematics being demonstrated. It is worth noting that my description below is based on my memory of what happened (I did not take detailed notes) and so hopefully I have represented Grace’s work well.
Grace started by showing something similar to the following expressions:
- 3×4 + 9×3 + 9×3 + 5×3
- 2×(9×3) + 9×4
- 5×10 + 2×(3×4) + 4×4
She described what the purpose of the activity was, and then uncovered three diagrams (similar to the ones below) which she said corresponded to the calculations of area already given. The fourth diagram she uncovered later.
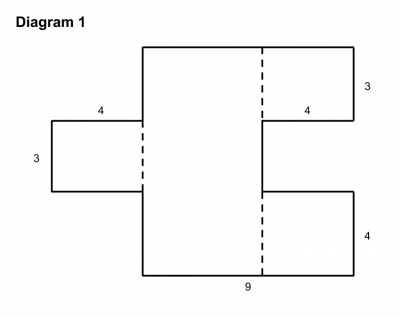
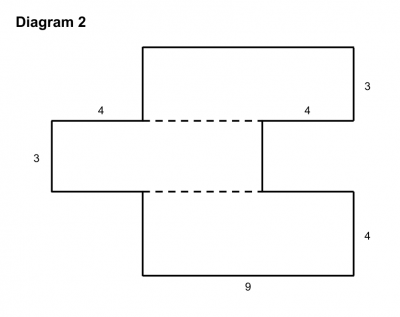
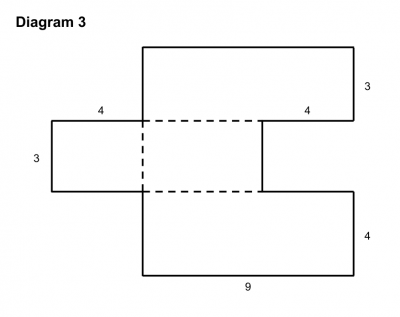
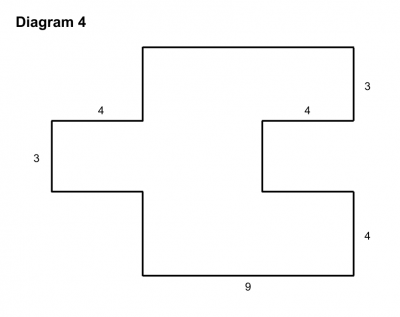
First she asked someone in the audience to explain which expression corresponded to the first diagram. While someone explained why the diagram and the expression were related, she carefully underlined the “chunk” of the expression which corresponded to the “chunk” of the diagram and shaded in the related portion of the diagram using the same color.
She then asked students to work with a partner to figure out which expression corresponded to the first diagram and why. Once students (in this case our teachers) had time to work this out, she asked two different pairs of students to come up to explain their reasoning. One partner was allowed to point but not talk and the other partner was allowed to talk but not point. Together they had to explain how they found a relationship between the expression and the diagram and color in the diagram and underline the expression in the same way. Grace repeated this process three times, once for each diagram.
She unveiled the blank diagram and asked participants to think of another way of cutting it up and then constructing the corresponding expression for their version of the diagram. She had someone come up to explain another way of looking at the expression using the blank diagram and construct their own corresponding expression, again asking them to ensure that they used color to relate the diagram and the expression.
Finally she summarized what each group found and asked if anyone saw any generalizations they saw between the different solution methods that were used.
Further support for students
Grace then went on to articulate five instructional strategies she used during the workshop that help support students in understanding the mathematics.
- Think-Pair-Share
- Annotating
- Sentence Starters and Frames
- Repetition
- Meta-reflection
She ended her presentation with this terrific comic from Michael G. Giangreco.

(source)
My reflection
Grace’s workshop took place in a room with about 130 teachers and I observed the diagrams from the opposite corner of the room. What I noticed is that even though I could not hear everything that was said, I was still substantially able to follow the mathematical arguments being made. I attributed my ability to follow the mathematics to the strategic use of color, the repatition in the diagrams, the use of gestures by Grace and the “students” who came up to present, and of course my existing understanding of the principle being focused on.
I also noticed that at no point did anyone actually talk about or calculate the final area. It was not that the final area was not important but that in this context, my suspicion is that it would not have contributed to the conversation, which was focused on the strategies and processes one could use to find the area. Grace was also careful not to introduce “the best way” to cut up the diagram to focus on students making sense of the relationship between the different ways of slicing up the shape given and the expressions given.
Students were not expected to come up with their own way of cutting up the area (which in my experience many students find challenging) or of creating an associated expression until they had listened to three different representations and been required to think about each diagram themselves.
A follow-up activity
As the workshop unfolded during the day, I thought of an activity that one could do on their own to follow up on the first part of the workshop. The purpose of this activity is two-fold; to understand different approaches to solving mathematics problems and to better understand the standards for mathematical practice.
Take a given mathematics problem (like this one) and construct a solution that emphasizes the use of MP2, another solution that emphasizes the use of MP7, and yet another solution that emphasizes MP8. Look at all three solutions and look for similarities and differences between the solutions. Think about how you would support students in understanding how to construct any one of the solution pathways you constructed (or in supporting students to construct their own solution pathways using MP2, MP7, or MP8).
Update: Here’s an example of the same task done in three different ways.
I solved the same task three different ways, attempting to use SMP2, 7, and 8 respectively. Thoughts? #mathchat pic.twitter.com/m8LY3QJQug
— David Wees (@davidwees) November 10, 2014
Elaine Watson says:
David,
Great summary of Grace Kelemanik’s presentation. Thanks for sharing. This is one of the best descriptions of the Practice Standards at work that I have read. I like your idea of the follow-up activity that isolates the approach to a problem using difference Practice Standards. Thank you for a great post!
November 11, 2014 — 10:53 am