For the last two years, the project I am currently working with has been asking teachers in many different schools to use common initial and final assessment tasks. The tasks themselves have been drawn from the library of MARS tasks available through the Math Shell project, as well as other very similar tasks curated by the Silicon Valley Math Initiative.
Here is a sample question from a MARS task with an actual student response. The shaded in circles below represent the scoring decisions made by the teacher who scored this task.

This summer I have been tasked with rethinking how we use our common beginning of unit formative assessments in our project. The purposes of our common assessments are to:
- provide teachers with information so they use it to help plan,
- provide students with rich mathematics tasks to introduce them to the mathematics for that unit,
- provide our program staff with information on the aggregate needs of students in the project.
We recently had the senior advisors to our project give us some feedback, and much of the feedback around our assessment model fell right in line with feedback we got from teachers through-out the year; the information the teachers were getting wasn’t very useful, and the tasks were often too hard for students, particularly at the beginning of the unit.
The first thing we are considering is providing more options for initial tasks for teachers to use, rather than specifying a particular assessment task for each unit (although for the early units, this may be less necessary). This, along with some guidance as to the emphases for each task and unit, may help teachers choose tasks which provide more access to more of their students.
The next thing we are exploring is using a completely different scoring system. In the past, teachers went through the assessment for each student, and according to a rubric, assigned a point value (usually 0, 1, or 2) to each scoring decision, and then totaled these for each student to produce a score on the assessment. The main problem with this scoring system is that it tends to focus teachers on what students got right or wrong, and not what they did to attempt to solve the problem. Both focii have some use when deciding what to do next with students, but the first operates from a deficit model (what did they do wrong) and the second operates from a building-on-strengths (what do they know how to do) model.
I took a look at a sample of 30 students’ work on this task, and decided that I could roughly group each students’ solution for each question under the categories of “algebraic”, “division”, “multiplication”, “addition”, and “other” strategy. I then took two sample classrooms of students and analyzed each students’ work on each question, categorizing according to the above set of strategies. It was pretty clear to me that in one classroom the students were attempting to use addition more often than in the other, and were struggling to successfully use arithmetic to solve the problems, whereas in the other class, most students had very few issues with arithmetic. I then recorded this information in a spreadsheet, along with the student answers, and generated some summaries of the distribution of strategies attempted as shown below.
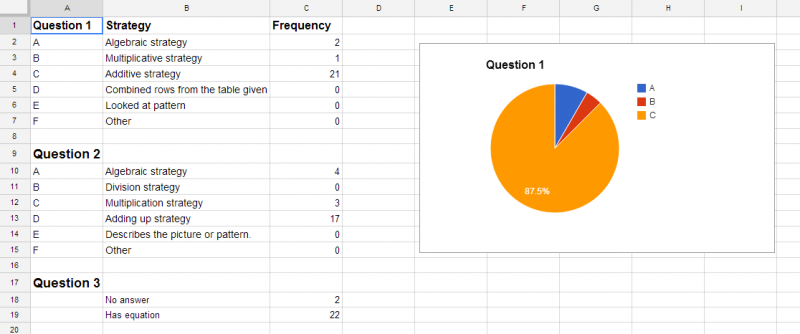
One assumption I made when even thinking about categorizing student strategies instead of scoring them for accuracy is that students will likely use the strategy to solve a problem which seems most appropriate to them, and that by extension, if they do not use a more efficient or more accurate strategy, it is because they don’t really understand why it works. In both of these classrooms, students tended to use addition to solve the first problem, but in one classroom virtually no students ever used anything beyond addition to solve any of the problems, and in the other classroom, students used more sophisticated multiplication strategies, and a few students even used algebraic approaches.
I tested this approach with two of my colleagues, who are also mathematics instructional specialists, and after categorizing the student responses, they both were able to come up with ideas on how they might approach the upcoming unit based on the student responses, and did not find the amount of time to categorize the responses to be much different than it would have been if they were scoring the responses.
I’d love some feedback on this process before we try and implement it in the 32 schools in our project next year. Has anyone focused on categorizing or summarizing student types of student responses on an assessment task in this way before? Does this process seem like it would be useful for you as a teacher? Do you have any questions about this approach?
Howard Phillips says:
At the end of the day someone somewhere is going to want a number attached to each student, so some form of scoring is unavoidable. Clearly it is not a good idea to abandon some sort of score for getting a more or less correct answer, and this should be scored independently of the method. I would then develop a scoring system for level of sophistication (or appropriateness) of the approach used, so for example if using algebra was considered the more “advanced” approach it would get more points than just adding up. Some fine tuning would be necessary, and probably some serious scaling.
I was surprised and concerned that none of the students looked at the pattern of the border to see that 5 more were needed each time. This says a lot about the general approach to the teaching of math.
Oh, and your illustractions, tables etcetera seem only to show the data from one of the two groups.
July 16, 2014 — 10:30 pm
David Wees says:
The need for a score is unavoidable, however, there is no need for a score for a task at the beginning of a unit, and in fact it is probably inappropriate. Instead, the idea is that the task (on a very closely related set of mathematics) at the end of the unit is scored, and can be converted into a grade for students as needed, but that hopefully we can convince the constituents of this system that a numerical score is not necessary for the beginning of unit.
I interpreted “5 more are needed each time” as a necessary understanding for a successful approach, but that some students basically thought of finding the answer as two additions, some students thought of 2 more in the pattern as being 10 more white hexagons (ie. they multiplied before adding), and a very small number of students created a linear equation to solve for the missing number. I wonder if they were not in a mathematics class if they would do this…
As for the data above, yes it is representative. With my colleagues, we have looked at four classrooms worth of student work, and we were able to categorize most approaches in the categories above, with only a small number of approaches not being easily described.
July 17, 2014 — 11:08 am
Eric Scholz says:
The greatest challenge I had was pulling relevant information out of the diagnostic. Beyond the first few Algebra IPATs, many students had a difficult time starting them because they did not have requisite knowledge. The IPATs were looking for requisite knowledge for the unit not the pre-requisite knowledge. If IPATs would be based on pre-requeist knowledge, we could identify which gaps existed in prior knowedge. Unfortunately, some of the necessary data to build successful re-engagement lessons would be missing because we would have to look for another point during the unit to give tasks to use for re-engagement.
I really like the idea for categorization and think it is viable for roll-out with a bit of professional development.
July 17, 2014 — 1:18 pm
Brandi Greathouse says:
I love the idea of looking at types of responses to gauge where students’ thinking is, but it seems like a daunting task to do this for all types of questions or skills taught. Am I missing something?
July 24, 2014 — 12:05 am
David Wees says:
You could do this during a class while students were working, but this is intended to be done once per unit at the beginning of the unit. We tested to see how long it takes to categorize 30 students work, and the results range from 15 to 25 minutes or so, which is not significantly different than if you were marking 30 tests for students. I think, given the information this process should give you, that it would be worth doing this.
One key aspect that is important to consider is that you wouldn’t have a gigantic assessment at the beginning of the unit with every possible variation of the core mathematics from the unit on it. You would have a two page assessment (see the MARS tasks for an example of these) that focuses on the core mathematical ideas of a unit.
July 24, 2014 — 4:44 am
Mary Dooms says:
Your pre-assessment strategy appears very doable. To differentiate, it may be helpful to identify the students for grouping purposes, i.e. column 1 for student name, column 2 for Q1 strategy, column 3 for Q2 strategy, etc. For columns 2 and 3 the teacher creates a key to identify the type of strategy (Al=algebraic, A=additive) and enters that into the cell. Then you can sort by column.
I really prefer your use of a task as a pre-assessment and examining the students’ strategies. I suppose one could also pre-assess the applicable math practices as well. When I pre-assessed it is much more skills based. I’d collect the data in Excel and I’d enter an x in the appropriate column if the student was proficient, i.e. column 1: student name, column: 2 rate, column 3: unit rate, column 4: ratio, etc.
I remember a tweet you sent me recently, “The farther away data is from the student, the less useful it becomes.” I hope your schools will embrace your suggestion.
July 27, 2014 — 7:56 pm
David Wees says:
I really like the sort idea. I can also fairly easily add filters to the data spreadsheet as well. Thanks for the suggestions. The aim is to keep the data as close to a record of what the students actually did as possible.
July 27, 2014 — 9:49 pm