Tag: mathchat (page 1 of 4)

March 20, 2012 / 4 Comments

Math in the real world: Gardening

My uncle called me today, and asked me a math question. Normally, I get called and asked technology related questions, but occasionally people remember that I have a mathematics background and call me in to assist.

My aunt wants to build a raised garden bed with a very particular shape. My uncle has been tasked with building it. She wants 3 of the sides of the shape to be 4 feet long, and the 4th side to be three feet long, and the whole shape should form a trapezoid (with a line of symmetry down the middle of the trapezoid). It took a little bit of chatting on the phone to get this to be clear, and I can see how being able to send each other pictures would have been really useful. To be able to build this shape as accurately as he would like, he needs to know all of the angles of the shape, so he can cut the pieces of the wood with the angles in the right position using a miter saw.

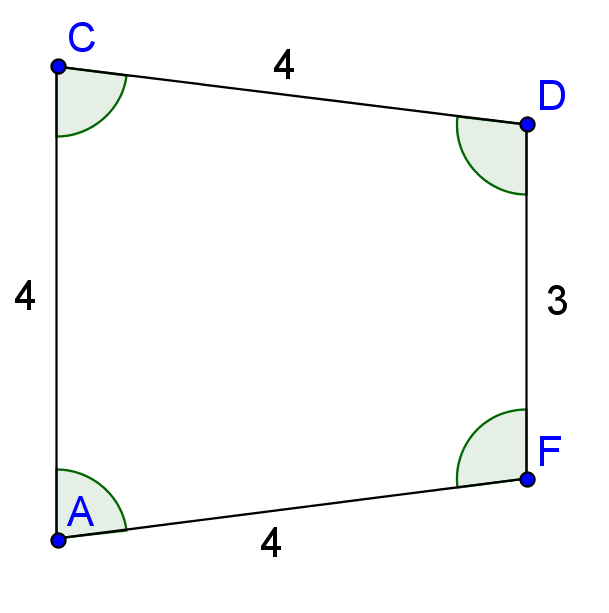
Trapezoid garden bed

I looked at the shape and decided that the fastest solution would be to build the shape in Geogebra, and measure the angles, which resulted in this.

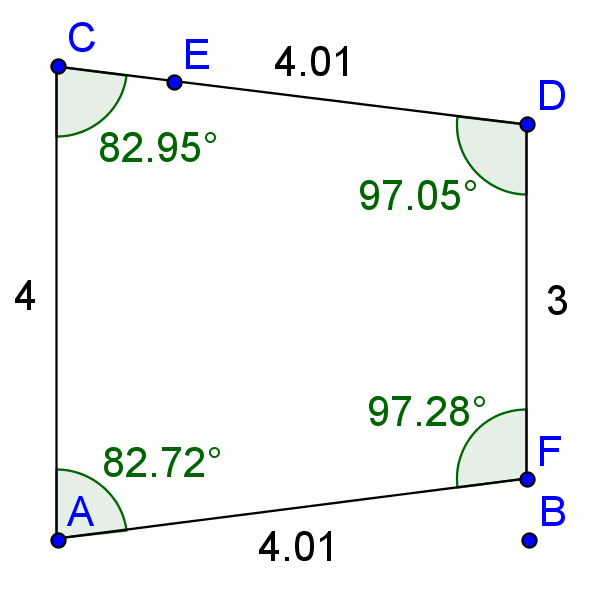
Not the exact solution, but close enough that my uncle would be able to use the miter saw (which has a maximum accuracy of 1 degree, according to my uncle) and cut the wood for his shape. It took me about 3 or 4 minutes to draw the shape in Geogebra and measure the angles.

After my phone call with my uncle was over, I decided that I should double check this solution though, and verify that I knew how to solve it.

I drew an imaginary line across the shape, and labelled that side x. This allowed me to create a pair of equations using the Cosine law, and I ended up with the following equation to solve:

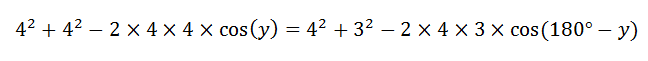
First equation

which simplifies to:

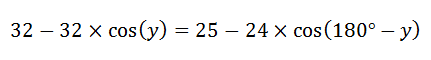
Second equation

and finally leads to this calculation:

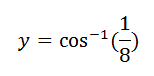
Third equation

On my calculator, that leads to a value of the smaller angle of about 82.8° and a larger angle of 97.2°, which means that my diagram that I drew for my uncle is fairly close. Wanting to be sure that my answer was correct, I also checked it using Wolfram Alpha, and on my graphing calculator.

After I told my uncle the solution, he told me that my aunt had suggested drawing the diagram carefully on a piece of paper and measuring the angles with a protractor, but he had complained that solution wasn’t "mathematical enough." Of course, this leads to a discussion of what it means to do mathematics, anyway.

Does it matter which way I solve this problem for my uncle? Which of these techniques would you classify as "mathematics"? All of them? None of them?

November 25, 2011 / 0 Comments

Mathematics in the real world: World Statistics

This is another post in my series on mathematics in the real world.

Thanks to a colleague of mine, I rediscovered the Google Public Data explorer. Within 10 minutes, I had constructed the above graph, which shows adolescent fertility rate for 15 to 19 year olds, versus life expectancy, measured against (look at the colors) average income for all of the countries in the world. If you click play, you can see a happy trend; life expectancy is increasing across the world for almost all countries, and the fertility rate is also decreasing.

This type of graph also lends itself well to questions from your students. For example, they may ask why so many teenagers have babies in some countries. They may also why there is a relationship (and from the above graph, it looks like the relationship is reasonably strong), between births from teenage moms, and life expectancy. They may also ask about trend itself, and why that is happening. Further, they may ask, how strong is this relationship? They may also confuse correlation with causation, which in itself can lead to an interesting conversation.

A natural extension of an activity related to this graph would be to have students construct their own graphs, perhaps even collecting their own data. What kind of social data do you think would interest your students?

October 30, 2011 / 3 Comments

Math in the real world: Marshmallow constructions

This is another post in my series of posts on math in the real world.

Building materials

My wife, son, and I went to a kids science event at SFU today, and at one table they had some marshmallow diagrams set up to demonstrate molecules. They let the kids play with the marshmallows and toothpicks, so my son made a giraffe. When we got home, he helped himself to some marshmallows and toothpicks and continued to make things with them.

Simple diagram

My son noticed that the most stable form included triangles (with some help from mommy), so he started to construct everything with triangles. When he moved into three dimensions, he noticed that the tetrahedron was the most stable of the forms he could build and so his construction soon began to look very mathematical in shape.

More complicated diagram

Now in his most complex form, he has started to build a three dimension tesselation. If he hadn’t been called away to dinner, or if we hadn’t been running low on toothpicks, I’m sure he would have continued the pattern.

Very complicated diagram

This activity involves both 2d and 3d geometry, tesselations, sequences and other patterns. Can you think of other mathematics that can be found in this activity?

October 18, 2011 / 9 Comments

Should we teach the standard algorithms for arithmetic?

Just posted this comment on this article lamenting the loss of the standard algorithms in Mathematics classrooms.

Should we teach the standard algorithms for arithmetic? Absolutely, but they shouldn’t be the only algorithms kids learn.

Why exactly is the ability to add, subtract, divide and multiply large numbers so critical? It seems clear to me that these are useful skills for numbers we will encounter in our day to day lives, and that it is useful to know that algorithms exist to work with larger numbers, but your other connections seem tenuous to me at best.

You’ve argued that without practice using algorithms, students will not be able to remember them to use them later, and this I agree with. It is a basic tenet of education that spaced repetition helps students remember how to use knowledge.

The question is, what type of knowledge is critical for students to remember? Does knowing how to multiple 39835 by 2338383 or any other arbitrarily large number assist the typical person in their life? Does it even contribute to a greater understanding of advanced mathematics? Has the number of people completing advanced mathematics degrees dropped? Statistics Canada data from 2007 suggests that it has dropped very slightly (see http://www.statcan.gc.ca/pub/81-004-x/2009005/article/11050-eng.htm) but not by an alarming amount.

Regarding your achievements as a PHD in mathematics, don’t forget, the plural of anecdote is not data. You can’t generalize from your one experience to what is useful for all of society.

Understanding how to use the algorithm seems sensible to me, but I think it is even more important that people understand algorithms (emphasis on the plural) which is probably lacking in the current curriculum as it is constructed.

One problem is that all across our society, at many different age groups, we have a lack of people using any advanced mathematical thinking to solve problems. If you look at how people solve problems similar to what they learned in school, but in a different context (see Jean Lave’s work), you find that it is rare for people to use the standard algorithms they learned in life, despite the fact that the standard algorithms are much more efficient than the various algorithms people construct for themselves. This suggests that even though the standard algorithms are more efficient, they may still not be the best algorithms to teach.

It seems to me that if over the course of a lifetime, some knowledge is going to be forgotten, the skill of learning is more important than what specific knowledge is learned.

Update: I’ve had another conversation with the author of the blog post above, and it seems I’ve over-reacted a bit. We have more in common than we disagree about.

October 18, 2011 / 1 Comment

Mathematical Modelling for Real – Exploring Mathematics

This playlist has some very interesting videos from the Open University on their YouTube channel on the topic of mathematical modelling, and how it is used in different contexts.

October 18, 2011 / 1 Comment

Eric Mazur: Memorization or understanding: are we teaching the right thing?

I recommend this talk by Eric Mazur on why he switched his teaching from lecture based teaching to peer instruction based approach. It’s more than an hour long, but it really is worth it.

How does this change how we teach? How much of what students learn in our classes is actually learned? If a student can only apply the concepts they have learned to very familiar contexts, and are completely unable to apply them in different contexts, can we really say they have learned the concepts?

October 18, 2011 / 17 Comments

I tried the Khan Academy

As an experiment, I started out the beginning of this year and tried flipping my classroom, but with a slight twist: I have extra instructional time, so students were to watch the instructional videos (from the Khan Academy and IBVodcasting.com) during classroom time. We spent about 1/3 of classtime using the Khan Academy videos and exercises, about 1/3 doing problem solving activities (like what is available on www.mathpickle.com and projecteuler.net), and the rest of the time attempting to put the knowledge we were learning into a useful context for the students. While students were involved in these activities, I spent my time circulating the classroom and providing individual and small group support and instruction.

After a month I ended my experiment and am currently in a state of transition while I explore other possible ways of running my classroom. Here are some of the reasons I ended it.

Some students chose, despite repeated requests from me, to only watch videos and do exercises that were really easy for them, instead of advancing their knowledge. One student said "she liked the easy videos because it was easy to get points." Another student said she chose the easy exercises because "she was worried about getting problems wrong." These students were more focused on getting easy points and avoiding challenges than learning.
Some of my students ignored the point system of the Khan Academy and focused on learning, but found that the information from the Khan Academy wasn’t challenging enough. When given practice questions from the course content, they found that the Khan Academy style questions didn’t adequately prepare them. This was partially addressed for these students by switching to the IBVodcasting.com videos, since they are more difficult.
A few students were able to "master" the content in the Khan Academy exercises after watching a few of the videos, but were unable to transfer what they had learned to any other context, and when queried in more depth, lacked basic understand of what they were learning. For example, they could solve problems like log10 + log2 = log20, but had no idea how to find the value of log20 in terms of p and q when log10 = p and log2 = q.

I’m hoping to implement the RME model and looking for resources that will help support the course curriculum I’m required to cover in the International Baccalaureate program. If I can’t find resources to support this, I’m switching back to my style where I spend some time with students doing experiments in math, some time working on practice problems, and some time with me explaining mathematical concepts. I’m definitely not using the Khan Academy videos again (but I will probably use the IBVodcasting.com videos as additional support for students).

See this Slideshare presentation for a description of what the RME model looks like.

What is Realistic Mathematics Education? National Mathematics Conference Swakopmund

View more presentations from jdewaard

;

October 13, 2011 / 8 Comments

When should we introduce kids to programming?

I recommend listening to this interview of Douglas Rushkoff on CBC Spark by Norah Young.

Rushkoff’s recommendation is that children should learn a little bit of a taste of programming right after they learn long division. His reasoning is basically this; once students see an algorithm like long division, and they learn how to make a computer compute long division for them, they’ll see that computers are devices which compute algorithms, not places for them to visit.

I’d like to add that teaching a computer to program something like long division would be very empowering for children. Having been through this process of learning what is one of the most complicated sequences of steps they’ve likely been exposed to in their young lives, they can then conquer this algorithm and "teach" a computer how to do it. As a happy consequence of teaching the computer the algorithm, they’ll probably understand how it works better.

October 13, 2011 / 4 Comments

Learning Origami

Origami swan

I started learning origami again this past weekend. So far I’ve built a swan, and a couple of paper airplanes that are more advanced than what I usually make but none of it has been particularly complicated to make. I’ve often thought that origami would be a fun hobby, but that I wouldn’t find much use for it in my teaching.

Today, I watched a TED talk (thanks to @BobbycSmith for sharing it with me today) that definitely changed my mind. Origami is way up there now on my list of things I need to learn.

October 12, 2011 / 4 Comments

Constructivist teaching is not “unassisted discovery”

I’ve been challenged recently to provide research which supports "unassisted discovery" over more traditional techniques for teaching math. This is not possible, as there are no teachers actually using "unassisted discovery" in their classrooms.

First, it is not possible to engage in the act of "unassisted discovery" as a student. Just knowing the language to describe what you are working on is a clear sign that at the very least you have the support of your language and culture in whatever you attempt.

Second, if a teacher has chosen the activity for you, or designed the learning objects you will be using, then they have given you an enormous amount of help by choosing the space in which you will be learning. Even Seymour Papert’s work with Logo was assisted discovery, after all, Logo is itself going to direct the inquiry toward what is possible to do with the language.

I can’t give examples of research which supports unassisted discovery, but I can give research which supports discovery learning in general. Without searching too hard, I found the following supportive research:

Bonawitza, Shaftob, Gweonc, Goodmand, Spelkee, Schulzc (2011) discovered that if you tell children how a toy works, they are less likely to discover additional capabilities of the toy than if you just give it to them, suggesting that direct instruction is efficient but comes at a cost: "children are less likely to perform potentially irrelevant actions but also less likely to discover novel information."

Chung (2004) discovered "no statistically signicant differences" between students who learned with a discovery based approach based on Constructivist learning principles as compared to a more traditionalist approach.

Cobb, Wood, Yackel, Nicholls, Wheatley, Trigatti, and Perlwitz (1991) discovered that students who learned mathematics through a project based approach for an entire year had similar computational fluency compared to a more traditional approach, but "students had higher levels of conceptual understanding in mathematics; held stronger beliefs about the importance of understanding and collaborating; and attributed less importance to conforming to the solution methods of others, competitiveness, and task-extrinsic reasons for success."

Downing, Ning, and Shin (2011) similarly found that a problem based learning approach to learning was more effective than traditional methods.

Wirkala and Kuhn (2011) very recently discovered that students who learned via problem based learning "showed superior mastery…relative to the lecture condition."

In a meta-study of nearly 200 other studies on student use of calculators in the classroom the NCTM concluded that "found that the body of research consistently shows that the use of calculators in the teaching and learning of mathematics does not contribute to any negative outcomes for skill development or procedural proficiency, but instead enhances the understanding of mathematics concepts and student orientation toward mathematics." (I’ve included this piece of research since many traditionalists oppose the use of calculators in mathematics education.)

Keith Devlin, in his book The Math Instinct, cited research by Jean Lave which found that people had highly accurate algorithms for doing supermarket math which were not at all related to the school math which they learned. In fact, people were able to solve supermarket math problems in the market itself with a 93% success rate, but when face with the exact same mathematics in a more traditional test format only answered 44% of the questions correctly. Later in the same chapter of his book, Devlin revealed more research suggesting that the longer people were out of school, the more successful they were at solving supermarket math questions.

It should also be noted that this discussion on what should be done to improve mathematics education shouldn’t be restricted to either traditional mathematics education, or discovery based methods, but that we should look at all of our possible options.