At the conference I was at in London, we were discussing, what would a mathematics curriculum look like if the computational step of doing mathematics was something students did using a computer?
Update: The video from this session has been posted by the Computer Based Math organization. See below.
Here are some objections shared by Conrad Wolfram and Jon McLoone at the Computer Based Math summit that happened in London, England. I just thought I’d add my two cents, and offer some more possible objections not in this list.
- You’ve got to know the basics first.
First, what are the basics, and why did we define them that way? Are they basic because the concepts are basic, or because they were discovered in a particular order? Are they considered basic because of computational complexity, or because of conceptual complexity?
Seymour Papert, in his book Mindstorms, suggested that much of what we teach in mathematics classes is the result of historical accidents. He also suggested that we teach some concepts, not because they are the most valuable to teach, but because they can be solved with paper and pencil.
- Computers dumb math down.
Jon McLoone has a terrific rebuttal to this argument. His basic premise: we’ve dumbed down mathematics education to limit us to what we are capable of doing with pencil and paper. I’d like to add that we have already turned mathematics education into sitcom-like instruction, where each topic can be taught in a single lesson (or a series of topics can be taught in a single unit), and where older topics are rarely, if ever, revisited. Having taught students how to use a particular topic, we then abandon it to learn new techniques.
- Hand calculating procedures teach understanding.
While I think that it possible that hand-calculating can teach something, too often I see people learn recipes for doing math, rather than actually learning mathematical reasoning. I don’t see this procedure necessarily helped by computer based math, but I don’t see that it is hurt either. Whether students do a procedure by hand, or by their computer, if they don’t understand the underlining concepts, they will struggle to use the mathematics in any meaningful context.
- We’re already doing it.
Really? There are some small pockets which are using computers as the tool for computation in mathematics, but not on any reasonable scale at the k to 12 level. Students do use calculators, but not consistently across the curriculum, and many potential applications of computers are not well represented by calculators.
- It isn’t math.
Here’s a diagram I’ve created to help capture the process of doing math.
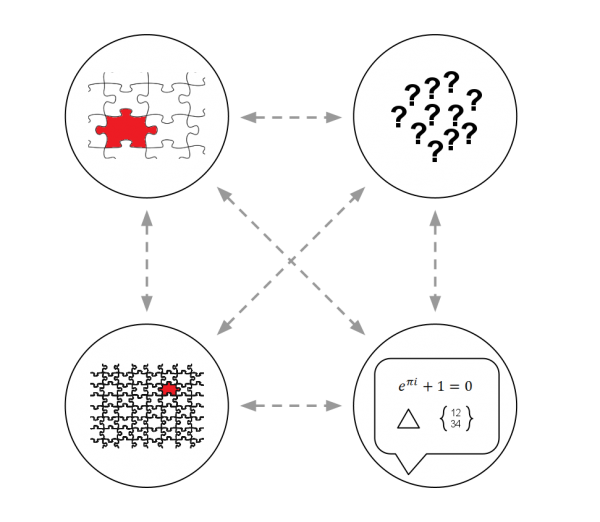
The big place in this process where computations happen is in the formulation (and sharing) step shown in the bottom right-hand corner. Note that actually doing the computation, according to this diagram, is only a tiny piece of doing mathematics. If you agree with my premise, that doing mathematics is more than the computations, you might be willing to accept that actually doing the computation step is a tiny piece of the mathematical process. Can we really say that students aren’t doing math if they hand-off that step to their computer?Do you think that children often get to do the entire process of math in schools, or are they often stuck at the computation step?
- You are making people over-reliant on computers.
I’d like to have students doing more of the mathematical process. Not everything lends itself well to using a computer, and these types of things will still happen in classrooms. Some concepts and ideas are actually not often taught in schools (such as the applications of origami to mathematics) and should be. I want to see students doing more thinking in classes, not less. Mathematics is not entirely in the tool one uses to do computations; most of it happens in the head.
So rather than seeing people be reliant on computers, I’d like to see some resources available (in the public domain) so that every computation students do on their computers has the "by hand" method carefully catalogged and available for students to use. I’d like to see the computations become part of a toolset, rather than what our students focus on learning.
- Traditional math is part of our culture.
I’d love to see mathematical history taught as an option in schools, so as to preserve the culture of mathematical tradition. That being said, culture changes, and we grow and adopt new traditions. For example, almost no one uses quill pens anymore, and it’s certainly not a skill we teach anymore in schools.
- Good idea – but it can’t be done.
People have already been teaching mathematics with computers as a tool for computation for a few decades now. I took a course myself in mathematical computation at UBC, and loved it. Rather than saying it cannot happen, since it has happened, we should look to see how we can expand and learn from the current iniatives.
Some further objections I can imagine people having:
- It isn’t fair; some students have access to technology, some do not.
This is one objection that I think has some merit behind it. We need to ensure that if we do move toward a model where computers replace the by-hand methods, we need to ensure that everyone has equitable access. As Seymour Papert (and others) have noted, a computer is only a tiny fraction of the total amount of money we spend on a student’s education, and so objections based on money seem to assume that we need to keep all of our existing structures, and that we can’t shrink some of them to pay for computers. How much money do we spend encouraging disengaged learners to remain in schools?
- It isn’t healthy.
It’s also not healthy to lack mathematical reasoning, literacy and analytical reasoning skills, but we let plenty of students graduate without these vital skills for life. We do need to balance screen-time versus other forms of more interactive and kinethestic learning, and this will be one of our challenges going forward in education.
What are some other objections you can imagine people having to this kind of change in mathematics? Can you extend my rebuttals to these objections?
