A few weeks ago, I spotted one of my students playing an interesting looking game on his computer, so I asked him about it. Turns out the game he was playing is called Portal (created by a company called Valve), and it’s still a fairly popular game today.
The basic premise of the game is that you have a special kind of gun which can create two portals, and your character can use these portals to travel instantly between two locations in the level. Each level of the game is a 3D puzzle that you have to solve. I decided tonight to look to see if I could find this game online, and I found this interesting 2D version of Portal, built in Flash. To really understand how the game works, I recommend playing it.
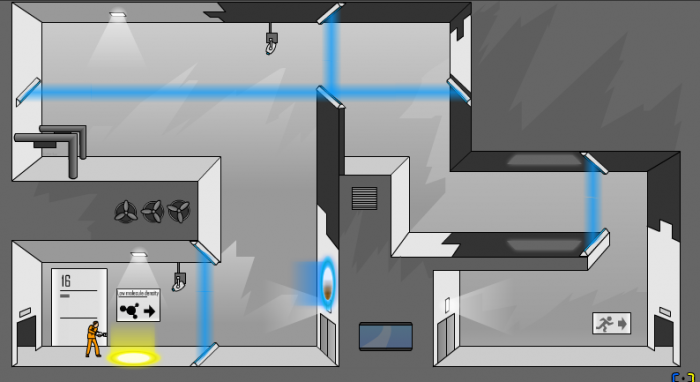
What I noticed, as I played the game, is that the puzzles are very much logic puzzles. You need to both strategize what a good move will be in the level, and also experiment a fair bit to figure things out. Every time your character dies in the game, you get to try over again to solve the puzzle, and so you get as many chances as you need to try to figure the puzzles out. Some of the puzzles involve a bit of reflexes, and some of them just involve some reasoning.

I also noticed that the portals themselves introduce a little bit of topological reasoning to the game. Once you start playing, you quickly realize that two positions in the game are equivalent, if there is an easy way to generate a portal between them. You also learn some tricks like the "infinite loop", where you create two vertical portals which you can fall through endlessly. Sometimes, I felt a little like I was playing Towers of Hanoi (itself a fairly mathematical game) because I would have to plan my moves ahead and choose the order of my portals carefully.
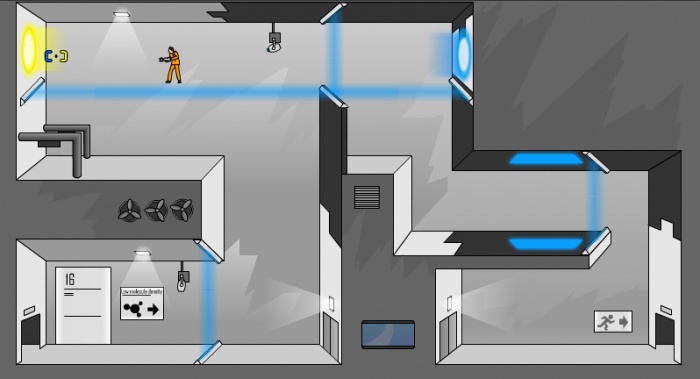
The perspective of the 2D version of the game is quite distorted (to allow for more surface area upon which to place one’s portals) and this got me thinking about perspective. "What’s wrong with the perspective in this game?" I thought. "Oh right, that wall and that floor are at the wrong angle with each other." The line of site of the portal gun also reminded me of intersecting lines, and I found myself visualizing the intersection of a wall and a line from my current position, and wondering if I was "going to hit that wall or not."
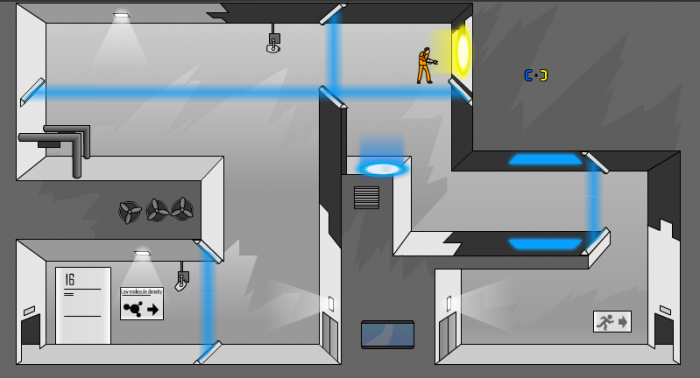
Timing is fairly critical on some of the levels. I found myself occasionally timing how long it took me to do an action, or a series of actions, so that I could time myself to be "in good position" to avoid a deadly (to my character) obstacle in the game. This is a little bit like algebraic reasoning, wherein I work backwards from one time and attempt to calculate (at least roughly) a good time to begin the sequence of actions.
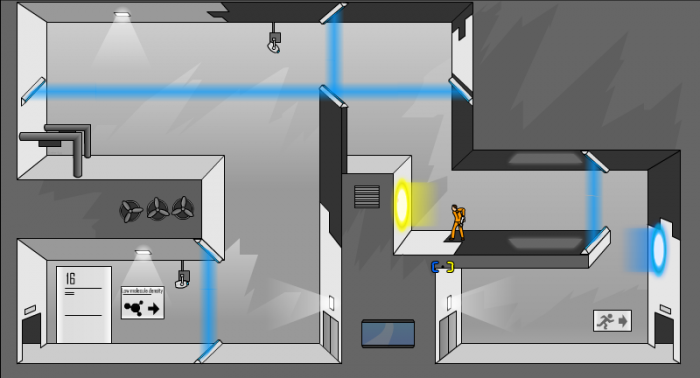
I experimented a fair bit, and would systematically move one of my portals a little bit each time, so that I could see how this changed the outcome of my movement through the portals. This is similar to a strategy used to solve some problems (and is a little bit like the scientific method) in mathematics. Sometimes to find a pattern, you have to build up representations in carefully thought out sequences, and the same is true in this game.
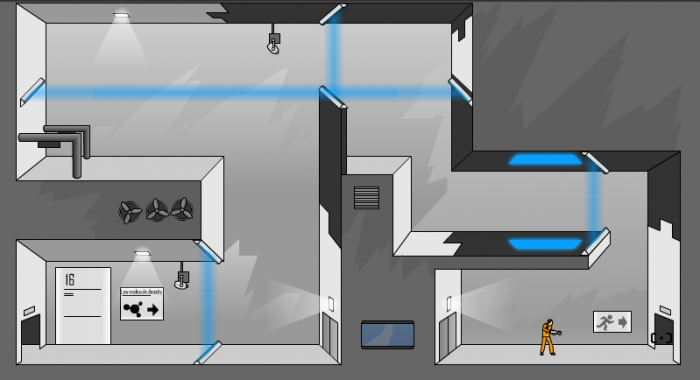
Portal is challenging like interesting problems in mathematics are. In the game, you can keep trying to work on the puzzle for as long as it takes. The only feedback you get from the game is the progress you have toward completing your goal, or (as often happened to me) your character’s death.
You could formalize some of the mathematical ideas that are part of this game, much in the same way that formalization of the use of Angry Birds to teach physics has been done.
I’d be interested to hear of anyone has some others on how this game could be useful in a math classroom, so please share any ideas you have.
Kayla Williams says:
David,
I am Kayla Williams and I am a student in EDM 310 at the University of South Alabama. I found your post to be very interesting and as a future teacher, I think this game would be very neat to use in the classroom. It would be a fun way to reinforce mathematical skills that have been previously taught. It would be a great way for students to learn and relate math to something that they probably use in their everyday lives.
October 9, 2011 — 9:17 pm
David Wees says:
I also see games like this, which contain some mathematics, as a sort of demonstration of what kinds of games you could make, and the potential for more "mathy" games to be created.
October 10, 2011 — 2:57 am
Jessy says:
This is very interesting game. I just downloaded it, gonna play it in my class as well. I hope teachers won’t go crazy about it:P
March 26, 2012 — 3:32 pm
Anonymous says:
Check out learningwithportals or teachwithportals . The company released an educator version of this.
July 11, 2012 — 10:56 am
David Wees says:
I saw that, and am planning on requesting an evaluation version, thank you for reminding me.
July 11, 2012 — 5:05 pm
Math Games says:
Thank you for sharing and reviewing the game.
I have developed a free mobile math game for Android, iOS and Amazon called “Numbers Planet”. It is a collection of many math games and number puzzles for kids and adults.
You can find it here on my blog:
https://ganaysa.blogspot.com/2019/01/numbers-planet-games-and-puzzles.html
I hope you like it.
September 12, 2019 — 8:29 pm