I’m currently working on math enrichment activities with some 3rd and 4th grade students. Aside from using some standard resources for enrichment, I’m finding that I can find challenging problems from different areas of mathematics and find ways to introduce the main concept to students in a context they understand.
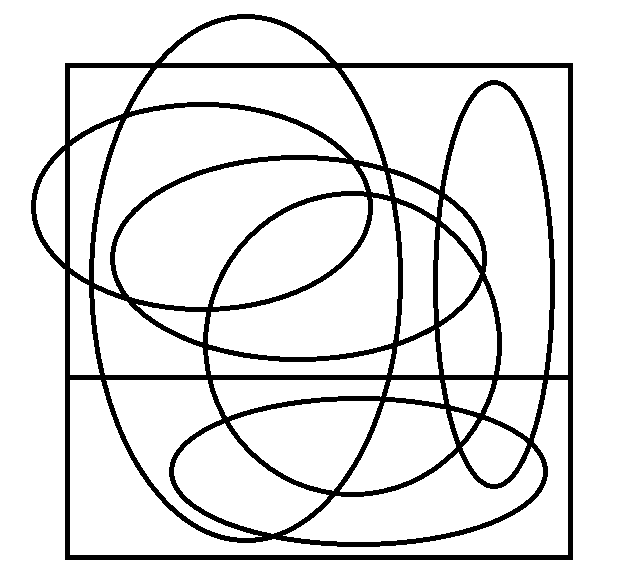
For example, our current question is, what is the minimum number of colours required to colour a map? The solution to this is well-known, but not in the circles 3rd and 4th graders hang out in. Here are some sample maps if you want to explore this on your own, or with your students (but I would recommend using real maps, at least to begin with, and then having students generate their own maps).
Here are some sample puzzles to get you (or your class) started. For each of the following maps, find the minimum number of colours to colour in the map so that no two adjacent sides are the same colour (countries which share a single point/vertex are not considered to be adjacent, only if they share an edge).
Puzzle 1

Puzzle 2
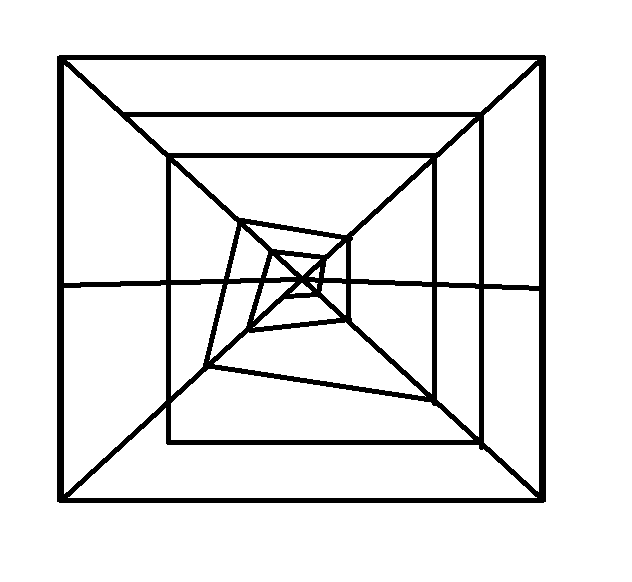
Puzzle 3