Year: 2019 (page 1 of 2)

Here is a video of Siegfried Engelmann demonstrating the mathematical learning of some children he worked with for a period of 1 or 2 years. Engelmann is one of the co-developers of a program called Direct Instruction, not to be confused with its cousin, direct instruction.

At the beginning of this video, Engelmann is careful to frame the video as a demonstration of learning rather than a demonstration of teaching, but it actually ends up being both. Engelmann, being a caring educator, cannot help but do a bit of teaching in this video.

 

 

Lesson analysis:

First, Engelmann builds up student motivation by presenting problems as challenging. He sets up students with statements like, “That’s pretty good, but pretty easy! Wait til you see this one.” When a student responds with a correct answer, he responds with, “Yay!” and then asks everyone to repeat the question and the answer. This kind of interaction is an ongoing theme throughout the video.

The students do not raise their hands, nor does Engelmann call on any students individually. Instead students call out answers as soon as they have them, so that often many different students call out answers together.

Next, Engelmann chooses specific sequences of problems to ask or pairs of problems that make some idea more clear through their variation from each other. For example, here is one sequence of questions:

1. What’s 8 plus 2?
2. What’s 10 plus 2?
3. 12 plus 2?

And here’s another sequence:

1. 7 plus 2?
2. 7 plus 3?
3. 7 plus 4?
4. 7 plus 5?

Choosing a sequence of problems to answer to elicit a particular strategy or idea is a reasonably common strategy in teaching, sometimes called a Number String or Problem String.

After nearly every question, the students respond by repeating the question and answer in unison, something they have clearly been taught to do. Underlying this strategy is presumably the belief that all children should be expected to participate in some way in class. Doug Lemov would call this, No Opt Out, and others have referred to it as holding high expectations for students.

Engelmann also circles back to previous problems students have done, increasing the connections students might make between problems. About 1 minute after students solved the problem “7 + 4 = ?” verbally, Engelmann writes the following on the board for students to solve.

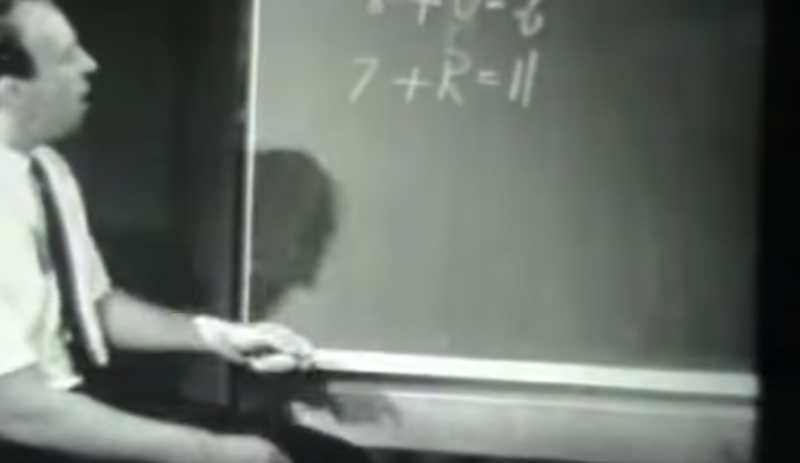
While Engelmann does not make the connection between this problem and the one students solved earlier explicit, it’s not likely to be an accidental choice of problem, given how deliberately the problems appear to be selected through-out the video.

Students frequently can be seen to be counting to find the answers to the question, a practice Engelmann makes no effort discourage, in fact he prompts it as a strategy at one point during the video.

Throughout the video, the children are exuberant and excited to be participating in this lesson. I did not notice any times when children seemed “off task” or disruptive, except perhaps towards the very end of the session where some of the children appear a bit tired.

At one point Engelmann makes a deliberate mistake, a common strategy used by teachers, and three of the children run up from their seats to correct the mistake for him, which ends up being part of the fun of the lesson. He also models how he responds to making a mistake and being corrected by the students — it’s no big deal.

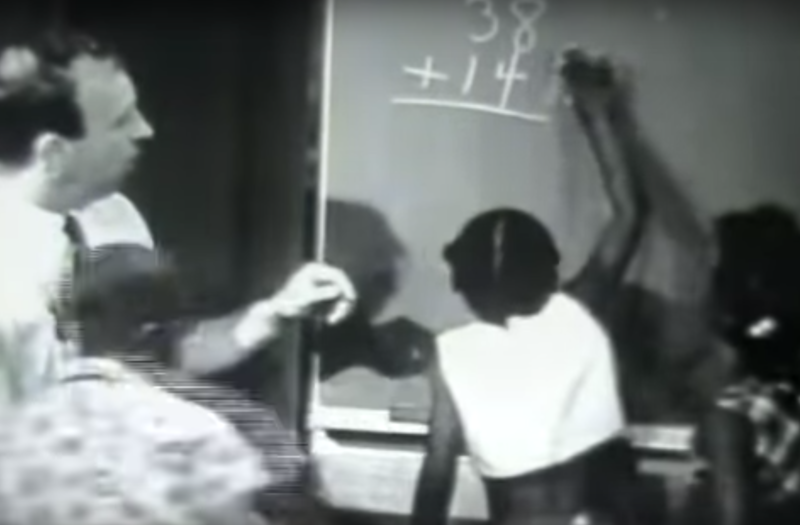
Engelmann pays careful attention to the language he uses. There are no tricks, no shortcuts, and no mathematical imprecisions. For example, in working through the example of 38 + 14, he is careful to refer to each digit by its place value meaning, so instead of saying 3 plus 1, he says 30 plus 10.

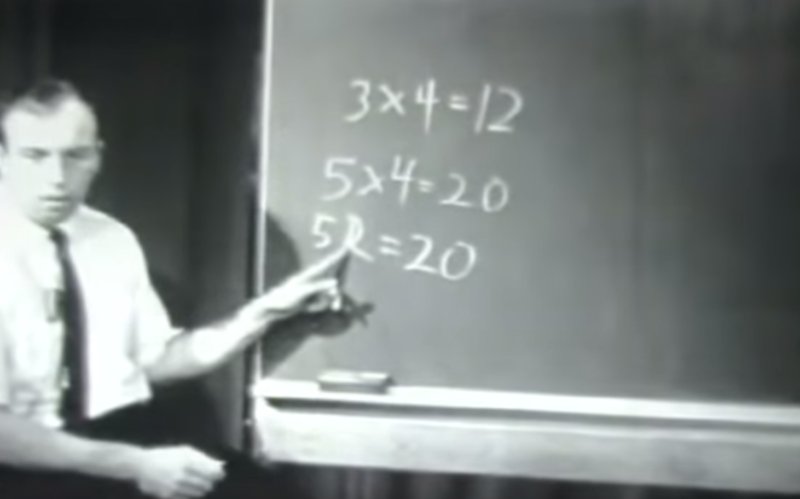
Engelmann asks many questions during the lesson. At one point, he asks, “Why can’t I erase the R here and put a 4?” which is likely intended to highlight the distinction between 54 and 5 × 4. Notice how he has both examples visible for contrast and that he is using an iconic gesture to emphasis what he is talking about with his question.

At one point, Engelmann draws a rectangle and marks it 3′ by 7′ and then asks students, “How many squares would be in this shape?” One of the student starts thinking out loud and says, “Okay, count by 3s. Count by 3s seven times.” The next problem he writes up he uses the same rectangle and relabels the sides 4 and c and marks the area as 24. He then asks students to figure out what c must be.

Two of the students call out 5, then another student calls out 6. Engelmann responds with, “Is that right?” as the students say 5 and then “6 is right!” when a student says 6. Engelmann then prompts students to “count by 4s how many times to get 24” as other students join him and repeat his instructions. As a group then, the whole class counts by 4. No students are singled out when they make mistakes, but no mistakes go without feedback either.

Near the end of the learning demonstration, Engelmann gives a fairly challenging problem.

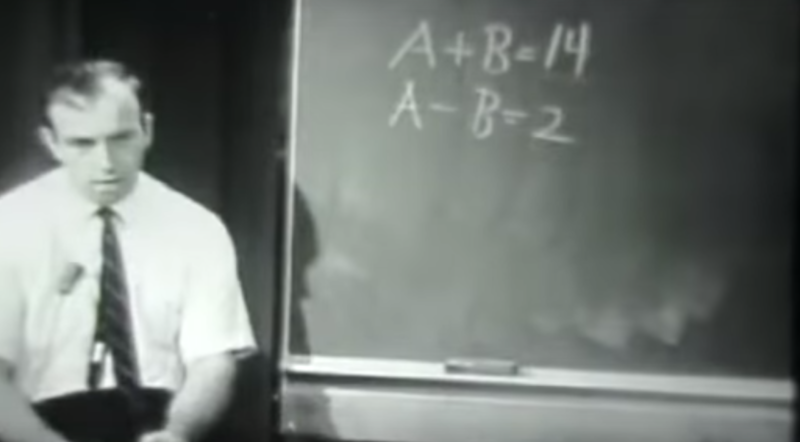
Engelmann waits 20 seconds before taking any action other than just watching the children think. Instead of telling students the answer or giving them a strategy, he changes the problem.

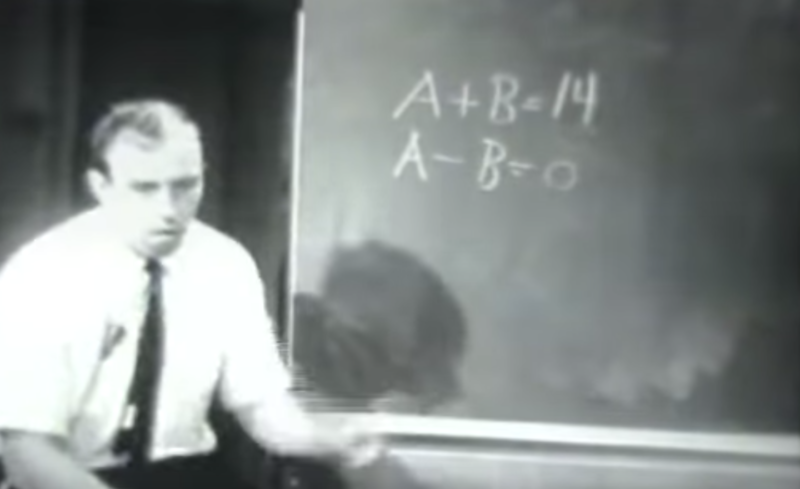
Students figure out the revised problem, and then Engelmann puts the original problem back up on the blackboard. He then waits again, this time for 18 seconds. This amount of wait time is remarkable given that most of the evening, Engelmann usually never waits more than a second for students to respond. Finally a student responds, and Engelmann congratulations the student and shares their answer with the class.

The class ends by Engelmann thanking the students for their participation and shaking each students’ hands.

 

Additional observations:

• Engelmann makes very little use of representations other than the symbolic although the students use their fingers as a tool many times.
• During the video Engelmann does not tell students exactly how to solve any of the problems, although he is fairly leading in one instance. It may be that this prohibition exists to make it easier to demonstrate the learning of the students and it may also be that explicit explanations are actually rare in his teaching.
• The pace is fast and variety of different arithmetic topics demonstrated through out the session is fairly large, but most of the numbers Engelmann uses are single or double digit numbers that students can still count with. The bulk of the mathematical work is on thinking about addition and subtraction in various ways with multiplicative ideas coming up as “counting by groups” or repeated addition.
• Engelmann makes use of a number of strategies also recommended for teachers to use with inquiry-oriented instructional routines suggesting that these strategies may be lesson-type agnostic.

 

Watching this lesson was a very different experience for me than most of the direct instruction I have observed. In fact, the experience was so different for me as to leave me unsure what relationship, if any, exists between typical direct instruction and what was intended by Engelmann as direct instruction?

Here’s a video of my son practicing at the playground. Prior to this, my son had already spent about five minutes trying to accomplish the same task.

 

I have two questions now after seeing my son practicing at the playground:

• How is this practice different than what practice typically looks like in math class?
• How can we make practice in a math class more like practice at a playground?

Children think with their minds, not with their hands. So when we assign activities because they are “hands on” it is more appropriate to think of these activities as being “minds on”. But of course, our minds are always on (to some degree) so now we want to specify, what exactly is it that is different about this task and what do I hope children will learn from this activity that they cannot learn without this activity?¹ Or alternatively, what does this activity allow that another activity might not?

For example, giving kids algebra tiles doesn’t mean that they will learn something important from using those algebra tiles. They might, but they might also learn the same thing from a structured activity using the area model.

My experience is that when I have vague hope that children will learn something from an activity that is related to the mathematics I want them to learn, they usually don’t.

To be clear, I see nothing wrong with students playing with manipulatives when free play is the goal. Sometimes having vague goals and experimenting with the use of manipulatives as a teacher is a good starting place for thinking about learning, but we should not conflate the ability of manipulatives to support learning with the actual learning students do as a result of using them.

 

References:

Visual patterns are a way to introduce and extend students’ understanding of algebra and functions. As such, there are a number of principles for helping students better understand algebra by examining visual patterns that have the same structure as their algebraic counterparts.

 

Principle #1: We can use the visual pattern to give more meaning to the algebraic structure.

What do you see changing in the pattern below? What stays the same? How is this pattern related to algebra?

In the pattern above, children are likely to describe the squares as growing from left to right. They’ll notice that the diagonals of the squares are shaded and that the squares are two longer each time.

Each of these observations can be described in terms of equations based on the term number. For example, a child might notice that each square has 4 arms and 1 center square shaded, so you might annotate the diagram to show the arms and the center square.

Another child notices that the length of each arm is one more than the term number and that the total number of black squares is 4 times this length plus one additional square. Algebraically, this is represented with S = 4(n + 1) + 1. We color the parts of this equation to correspond with the visual to make the connections more clear. By doing this, we assign meaning to each part of the expression based on the visual.

 

Principle #2: We can use visual patterns to justify algebraic relationships.

Visual patterns can also be used to give meaning and to justify that a particular algebraic relationship is true, beyond what is possible to do with pure algebraic reasoning alone or a single visual example.

One might start by giving students the following image and asking them what they notice about the image.

Collectively, students will notice that there are five squares, each square is larger than the square before it, each square is composed of smaller squares, each square has the square before it embedded in the lower left-hand corner, the number of white squares added on each time is odd, and a whole of other mathematical and non-mathematical observations.

The observation that each square is embedded in the next square and that the number of white squares added each time is an odd number can be written as follows.

1² = 0 + 1 = 0² + 1 = 1
2² = 1 + 3 = 1² + 3 = 4
3² = 4 + 5 = 2² + 5 = 9
4² = 9 + 7 = 3² + 7 = 16
5² = 16 + 9 = 4² + 9 = 25

By starting with the visual, students can reason inductively that “each square is just the square before it plus an odd number” and then this reasoning can be represented algebraically as n² = (n – 1)² + (2n + 1).

 

Principle #3: Visual patterns can be used to help students understand some of the language used in algebra.

I did not learn during high school why “Completing the Square” was called Completing the Square. It wasn’t until I started teaching the idea using a visual to represent the square² that the language made sense.

 

Principle #4: Visual patterns can be used to distinguish between different algebraic functions³.

Look at the two patterns below. How is each pattern changing as it increasing? How are these changes different between the different kinds of visuals?

By using patterns we can more easily contrast the difference between y = 2x and y = 2^x which in written form are far more similar the corresponding visual sequences.

 

Further resources and inspiration:

• From Patterns to Algebra
• Connecting Arithmetic to Algebra
• Visual Patterns
• Routines for Reasoning

 

Misconception: a view or opinion that is incorrect because [it is] based on faulty thinking or understanding⁴; a wrong or inaccurate idea or conception⁵.

These two definitions for misconceptions vary slightly, but the gist of the definitions are the same — there are some ways of thinking which do not match the world as we know it.

When we examine children thinking closely, we find that thinking often differs from our own. But this makes sense given that children have different experiences of the world than we do and often have not experienced the parts of the world that we have.

What should a teacher do about misconceptions? Should teachers try to prevent kids from having misconceptions? Should teachers label children who have misconceptions as wrong? Is there any harm in labelling children’s ideas as misconceptions? ⁶

It’s clear that some ways we use language to talk about children cause harm. If I consistently use the words “low” and “high”⁷ to describe my students, then the odds are greater that I also associate low and high expectations for these groups of students, which is correlated with student learning⁸. Here the language is harmful because it over simplifies the relationship between children and their background knowledge and results in students learning less than they would otherwise be capable of learning.⁹

The most problematic nature of the idea of misconceptions is that it frames how we respond to children’s ideas.

1. A child writes 2 × 3 = 5 when they meant to write 2 × 3 = 6. Why did the child do this? Maybe they were overwhelmed with the task or tasks they were working on and defaulted to a previous relationship they know. It’s not a misconception per se, it’s something the child could probably find for themselves if asked to look at their work again.
   
2. A child looks at the two angles below and concludes that angle A is larger because the rays are longer. This definition of larger is likely to be entirely consistent with every other experience of smaller and larger for this child. This child is attending to different properties of the geometry than the one intended by the author of the question.
   
   Is this a misconception? Or is this an entirely consistent worldview based on a different world than their teacher? Do we say to the child, “No, that’s wrong,” or do we value the thinking this child did and consider how to increase the size of their world?

My preference when working with children is to avoid over-simplistic words and phrases to describe their thinking. By default, the word misconception assumes a deficit view of children’s thinking¹⁰ and ignores the great thinking children did to come up with their ideas. What I prefer to the word misconception is language that describes more precisely the varied ways of thinking that children have. While it is the role of teachers to expand the world view of children and we need language to talk to colleagues about our role, the language we adopt frames the conversations we have.

 

I can remember exactly where I had my first major mathematical discovery. We were driving up the highway toward the nearby town for a night out for dinner. I was sitting in the back of the car playing with sums of numbers in my head.

1 = 1
1 + 2 = 3
1 + 2 + 3 = 6
1 + 2 + 3 + 4 = 10
1 + 2 + 3 + 4 + 5 = 15
1 + 2 + 3 + 4 + 5 + 6 = 21

I noticed something strange about the sums with an even number of terms.

1 + 2 = 3 = 2 × 3/2
1 + 2 + 3 + 4 = 10 = 4 × 5/2
1 + 2 + 3 + 4 + 5 + 6 = 21 = 6 × 7/2

“That’s weird”, I thought. “Each of those answers is just the last number in the sequence times half of the number after it. I wonder if that works for the odd numbers?”

1 = 1 = 1 × 2/1
1 + 2 + 3 = 6 = 3 × 4/2
1 + 2 + 3 + 4 + 5 = 15 = 5 × 6/2

“Wow! It works! Let me try it for a bigger number.”

1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 = 55 = 10 × 11/2

At that point, I cheered out loud and had to explain my discovery to my parents, who were now wondering what was going on in their back seat.

Two years later, I learned in my middle school math class that this specific relationship had been discovered by someone else before me. These sums I had been finding had a name, triangular numbers. I learned that an algebraic way of representing this relationship was S_n = n(n + 1)/2.

What I had not learned before this point was that real people invent mathematics. For all I knew, mathematics sprung up fully formed from the heads of my teachers. Mathematics was a god to me, my teachers were like Zeus giving birth to Athena, and I had no idea people were involved in the creation of mathematics at all.

There is an argument about what methods of teaching mathematics lead to students best knowing mathematics, but often lost in these arguments is what mathematics even is. Is mathematics a set of ideas? Is mathematics a process? Is it both? I spent most of my school career viewing mathematics as a set of concepts other people knew and would tell me. It was only in rare moments, like the one in the back of my parents’ car, that I got a glimpse of mathematics as something more.

It is possible to both teach mathematical ideas and mathematical processes. These two ways of knowing mathematics are complementary and not dichotomous. If one centers the ideas students have in class, then students learn both that their ideas matter and that they have mathematical agency.

But if one has never taught with the aim of centering student ideas, how does one get started?

Try watching this video of students engaging in an instructional routine called Choral Counting. The teacher starts with a quick discussion about pennies, and then the routine itself starts when the teacher gives students instructions on how they are going to count together. When you have time, watch the first six and a half minutes of the video.

You might be wondering how the counting-in-unison aspect of this routine centers students’ ideas, and I think that it’s a fair point to make. Note that the students do the counting and the teacher records what they say. While the thinking students do during this section of the routine is less obvious, that thinking enables students to have a count that they created together that they can analyze for patterns. At about 5 minutes and 45 seconds into the video, an individual student shares a conjecture and the class quickly tests this conjecture by continuing the count. By using annotation, gestures, and repeating what students have said, the teacher increases how much access students have to each other’s reasoning.

More importantly, these students get an opportunity at a fairly early stage in their mathematical careers to get a taste of the mathematical process of looking for patterns, coming up with conjectures and testing those conjectures while simultaneously building their understanding of place value in the decimal system.

It is unfortunate (and understandable, given privacy concerns) that this video shows only the actions the teacher takes and not the responses by students. There are some things I might do differently than this teacher but they and I agree on a critical point — students can behave as mathematicians and learn mathematics from the experience.

This next video example is truncated from a longer recording of a lesson from a middle school class and includes some thoughts from the teacher interspersed throughout the video. If you are interested, here is the link to the full-length video without the teacher commentary.

Contemplate Then Calculate: Grade 6 Telescoping Sums [14 minutes] from New Visions for Public Schools on Vimeo.

 

In this routine, Contemplate then Calculate, students are expected to delay any calculations until after they have stopped to look at the problem in some detail, a strategy that has a small amount of research to support it. A key difference between this routine and Choral Counting, besides the obvious differences in the structure and mathematical focus of the routine, is that Contemplate then Calculate has deliberate instructional strategies intended to support access embedded within the structure of the routine.

If efforts to humanize the mathematics classroom by surfacing the thinking of students do not include deliberate strategies to support the engagement of ALL students, then for some students this experience can be just as dehumanizing as many other math classrooms. If you do not feel included in the math classroom, then it cannot be a humanizing experience for you.

The most important idea here is that we can make the mathematics classroom a more inviting place and make mathematics itself more inviting by centering the ideas of students in the classroom. We can make this experience more humanizing for all students by using instructional routines that reduce typical barriers for entry for students and embed instructional supports within those routines that provide access to the mathematical thinking to all.

This post is part of the Virtual Conference on Humanizing Mathematics.

 

At a conference in Burnaby last Spring, the keynote speaker, Shelley Moore, shared a graphic similar to this one. The green circles are typical learners and the red, yellow, and blue circles are people with learning differences.

And then she made the observation that this graphic still promotes a problematic view of being inclusive and shared this graphic with us.

The key difference is that the updated graphic recognizes that there is variation between all of us. By using green to mean typical and the other colours to mean atypical, there is still a false dichotomy created between the two groups of learners. In a practical sense, many disabilities are defined by an arbitrary line drawn on a measure of the range of human ability.

But, we should not ignore the diversity in our learners. Some learners really do need different supports than others. The key is to recognize that many instructional supports intended for some learners are actually helpful for all learners.^1  2

All students benefit from sufficient time to think and to process. All students benefit from a public record of what is being discussed. All students benefit from making mathematical ideas explicit. All students benefit from teachers who have high expectations for their capacity to learn.

 

1. A side note here: there are a small number of disabilities people have which do require very different supports that are unhelpful for other students. In those cases, using targeted support is warranted provided one does so while recognizing the learners are part of the varied tapestry of humanity.

2. These ideas around inclusion for all are also a central theme of the book, Routines for Reasoning.

 

What do you notice and what do you wonder about this diagram representing the process of mathematical modelling?

source)

The image above is from a description of mathematical modelling as part of a course intended for students at the university level.

Unfortunately, the image below is how much mathematical modelling occurs in math classes before university.

Sometimes some of the steps for modelling are done for students, leading to processes that look more like this.

Dan Meyer has written and presented a fair bit about reclaiming the first three steps in mathematical modelling, however, a critical difference between the typical processes used in mathematical modelling in k-12 mathematics and after k-12 mathematics is the time spent iterating on and improving the mathematical model (and in many cases, the technology used to calculate whether the model is successful).

In other words, we need to replace the “better luck next time” step with more opportunity for iteration. We want students to be able to look at the model they construct and predict the behaviour of that model. We want students to have the ability to see the results of their model and then revise their model to more closely match their data.

Here’s a tool for modelling distance versus time graphs that I created a while ago. Notice how it gives the students the opportunity to abandon their current model (how quickly and/or in what direction they drag the little stick person) and start again with a different model.

Another way that we can give students opportunities to revise their model that does not require technology is to use instructional routines that embed unpacking an alternate model and then turning around and trying to apply that new model to students’ previous work.

The key idea is that in most mathematically modelling, coming up with the initial model is just the first step; after this students need opportunities to revise their models and iterate until they have a model that best represents their data (and ideally, a rationale for why this model works the best).

 

I do not think that anyone believes that children are machines, but the analogies people use to understand how children learn and consequently, how one should teach children are often based on children’s minds being like a computer.

 

Minds do not store information

When we experience the world, our minds are changed in response to our experiences, slowly, gradually, over time. We build pathways in our brains so that we can re-experience the world and in doing so, build responses for the next time we are faced with a similar experience.

Our brains have, through the process of evolution, developed the habit of keeping experiences that we revisit frequently and over time, and trimming neural connections corresponding to the less frequent (and from an evolutionary stand-point, less useful) experiences. We call this process forgetting but it is worth knowing that it happens quickly — within an hour of experiencing something we can no longer re-experience most of what we experienced (eg. we’ve forgotten it).

One might say that our brains store representations of what we have experienced, but unlike a computer hard drive, these stored representations change over time. Also, these representations are generally highly inaccurate, relative to the actual objects themselves.

Try drawing, in as much detail as you can without looking at the object, some common fruit from where you live. You’ll invariably find that what you can reproduce without looking at the object is far less detailed than the object itself. Our brains, at best, store sufficient detail (as encoded in neural pathways that allow us to “re-experience” seeing the object) to be able to recognize that object again in the future.

At best we store experiences of objects in our head that are minimally sufficient to be able to recognize those objects in the future. It is possible that even with increased exposure to these objects, our internal representations may never become more accurate.

 

Learning is not performance

Several years ago, I taught a Saturday class that contained my son and about 8 of his homeschool friends. The goals of that particular day were to develop students’ ability to recognize that fractions are numbers, that fractions can be represented on a number line, and that we can use the number line to look for equivalence between fractions.

Toward the end of the lesson, when asked what fractions 3/4 is equivalent to, my son told me, “One third because the 3 in the denominator tells you how many quarters there are.” It seemed clear that he had not learned what was intended by the lesson. (An aside: how could what my son said make sense, given his limited experience with fractions?)

However, I chose at that time to do nothing and basically wait. Two weeks later, with no intervening mathematics lessons from me, I asked him again, “Is 1/3 equivalent to 3/4?” and my son responded, “No, there’s no way! 1/3 is less than 1/2 and 3/4 is more than 1/2 so they can’t possibly be the same!”

 

Minds forget things

I have often heard teachers complain that students appear to have never learned some critical prerequisite idea from an earlier teacher. “Why don’t those elementary school teachers drill the times tables better! These kids don’t know their times tables.”

But there is a simpler hypothesis; children did experience those ideas with an earlier teacher but have since forgotten them. Or alternatively, children have trouble retrieving the ideas and rebuilding their experience of those ideas because of the delay in time between when children first experienced the idea and when they need it later. Much work is done with children to have them review and re-experience ideas they have experienced that might be better spent asking children to retrieve and relive those experiences instead.

If we want students to remember everything that was experienced, then we need to include time for students to practice, rehearse, relive, retrieve, and build connections between what is currently being experienced to what was experienced in the past. The Illustrative Mathematics curriculum that is referenced in the image above does this by building in practice problems for each unit that reference ideas from earlier units.

 

Memories are personal and change over time

A very long time ago, I remember being in middle school and listening to a girl describe why she fixed her hair the way she did. I obnoxiously retorted that her head was the only place she had hair. With my two friends present, she flashed me to prove to me she had hair elsewhere. Years later, I recounted this story to my friends and discovered that each of them believed they had made the obnoxious comment and were the one flashed.

Our memories not only change over time but how we re-experience events depends on what experiences we had before those events.

While children are experiencing ideas, it behooves us to listen to what they experienced from their perspective and how they attempt to connect it to their prior experiences. We have greater expertise and experience with the mathematical ideas than do our students, so consequently, the mathematical connections we make will be different.

 

Learning is long term change

A goal of teaching is not to change what students do or know for tomorrow but ideally what they know and can do for the rest of their lives. Consequently, teachers should be more interested in long-term changes in what students know and can do than short-term performances.

Reviewing the material children should have learned from a unit helps those children increase their performance on the assessment tomorrow but may hamper their ability to recall those experiences in the long term. Reviewing the material children should have learned from the past school year for three weeks before their final assessment might improve students’ performance on that assessment (although it probably doesn’t, given the scale of how quickly our minds forget experiences) but it definitely does nothing to support children in taking those experiences with them for the rest of their lives.

Instead of cramming all of the ideas for the year into a short unit at the end of the year, build opportunities for students to retrieve ideas from previous lessons regularly into every lesson. Instead of telling kids what they should have learned the day before an assessment, use structured retrieval practice with embedded feedback (two of my favourite sources of this kind of structured practice are instructional routines and these formative assessment lessons).

 

Children are not machines

Unlike machines, children do not store literal copies of what they experience. Unlike machines, children’s memories of those experiences degrade over time. Unlike machines, children benefit little from re-experiencing ideas and benefit greatly from actively re-living experiences from their memories. Unlike machines, what children remember from experiences is personally and highly dependent on what children had experienced earlier in their lives. Unlike machines, children take a long time to change — we can’t just install new software in children to change what they can do.

 

The last two years I have been working for New Visions for Public Schools, mostly remotely but with some trips to New York City to run workshops and do school visits. During that time, I’ve kept careful track of the work I have completed as you can see above.

With my colleagues, we completed an Algebra I course which includes:

• 5 videos to support specific instructional strategies
• 7 formative assessment lessons
• 8 units and 7 unit plans
• 7 initial tasks, 7 end-of-unit assessments
• 10 videos of instructional routines enacted in the classroom
• 24 Big Ideas
• 123 tasks to support instructional routines
• 125 interleaved, spaced, retrieval practice assignments
• 138 pages of notes for teachers
• 664 pages of student-facing materials (link 1, link 2)
• An add-on to help manage 1200 typeset Regents problems

These resources were built with support for multilingual students and students with disabilities baked in. We read and incorporated cognitive science in the development of these resources. We released all of these resources under a Creative Commons license so that teachers could feel free to download and adapt these resources for their students. In order to support teachers in using this curriculum, I personally spent over 650 hours preparing and enacting workshops for teachers over the last two years.

My work with New Visions is wrapping up soon and so I am reflecting on the work we completed. I regret that our Geometry and Algebra II courses are not yet done, but I feel pretty proud of what we accomplished together regardless.