What do you notice and what do you wonder about this diagram representing the process of mathematical modelling?

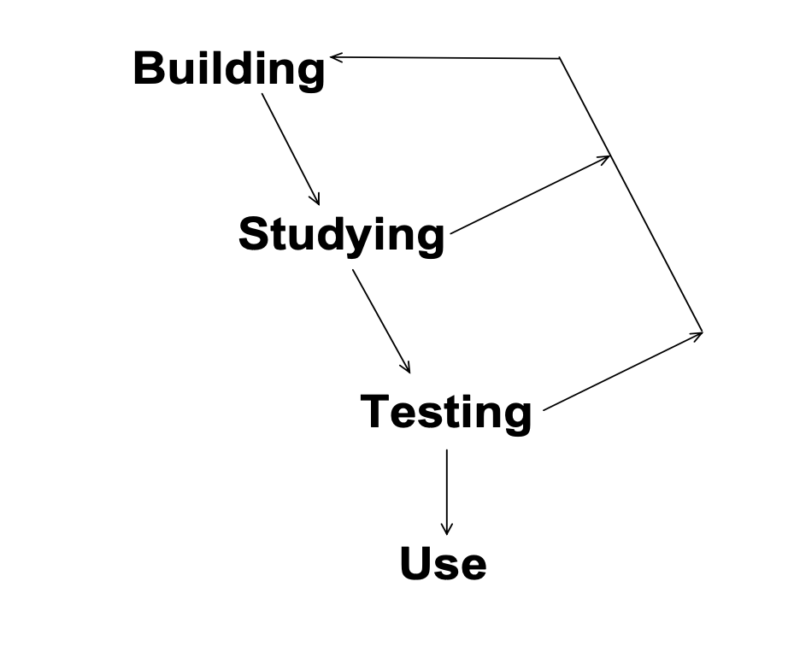Building => Studying => Testing => Use And iterate back to any step as needed.” class=”wp-image-2234″><figcaption>A diagram representing the stages of mathematical modelling. (<a href=source)

The image above is from a description of mathematical modelling as part of a course intended for students at the university level.

Unfortunately, the image below is how much mathematical modelling occurs in math classes before university.

(source)

Sometimes some of the steps for modelling are done for students, leading to processes that look more like this.

Only two steps for mathematical modelling -- solve the model, answer the question.
The two most common steps in k-12 mathematical modelling

Dan Meyer has written and presented a fair bit about reclaiming the first three steps in mathematical modelling, however, a critical difference between the typical processes used in mathematical modelling in k-12 mathematics and after k-12 mathematics is the time spent iterating on and improving the mathematical model (and in many cases, the technology used to calculate whether the model is successful).

Revised to include another common step: Better Luck Next Time

In other words, we need to replace the “better luck next time” step with more opportunity for iteration. We want students to be able to look at the model they construct and predict the behaviour of that model. We want students to have the ability to see the results of their model and then revise their model to more closely match their data.

Here’s a tool for modelling distance versus time graphs that I created a while ago. Notice how it gives the students the opportunity to abandon their current model (how quickly and/or in what direction they drag the little stick person) and start again with a different model.

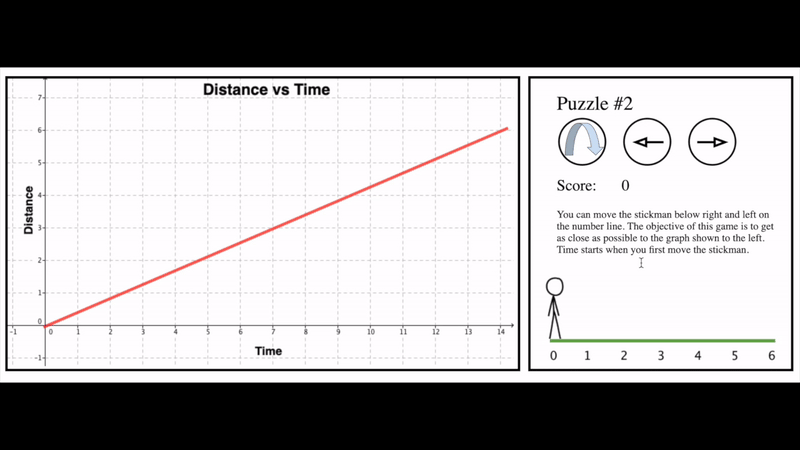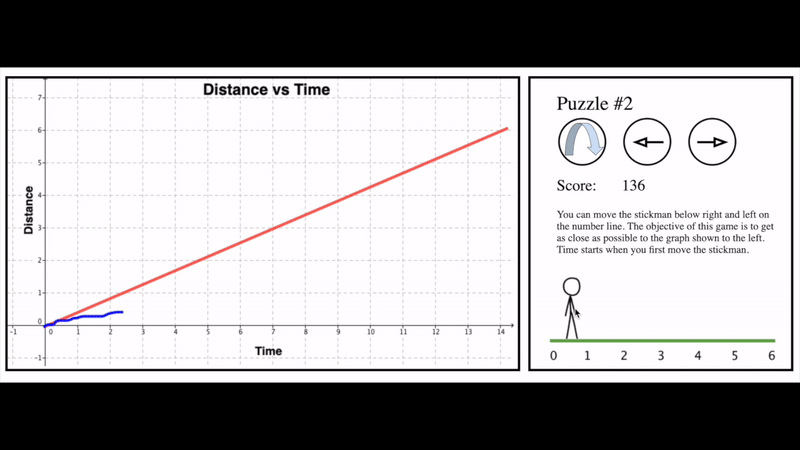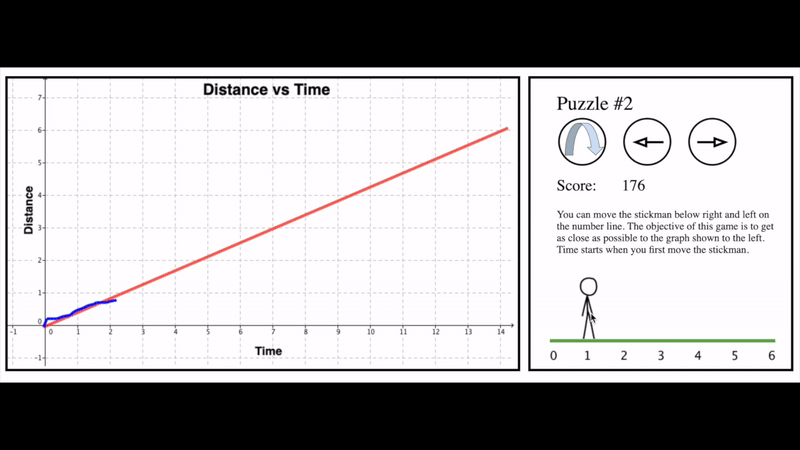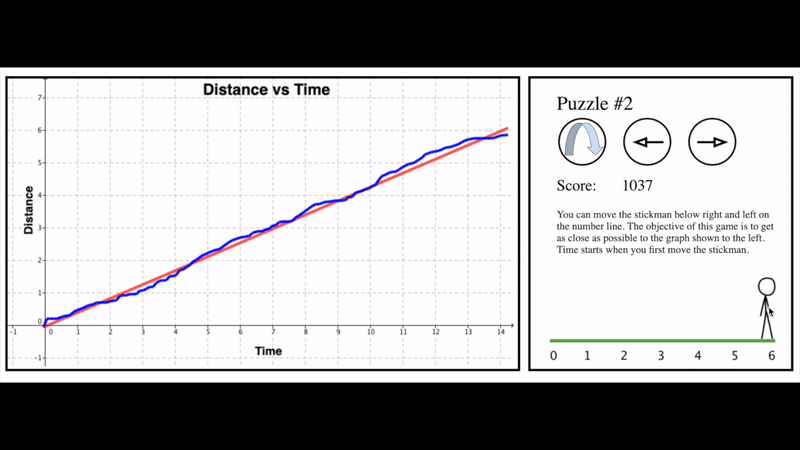
It may take several attempts to pick a model that works.

Another way that we can give students opportunities to revise their model that does not require technology is to use instructional routines that embed unpacking an alternate model and then turning around and trying to apply that new model to students’ previous work.

The key idea is that in most mathematically modelling, coming up with the initial model is just the first step; after this students need opportunities to revise their models and iterate until they have a model that best represents their data (and ideally, a rationale for why this model works the best).

 

Facebooktwitterredditpinterestlinkedinmail