In 1992, Deborah Loewenberg Ball wrote an article called Magical Hopes: Manipulatives and the Reform of Mathematics Education. This article is intended to draw some connections between our use of manipulatives and our use of technology in math education, and hopefully offer some suggestions for improving the use of technology.
There is a similar magical hope that technology can be used to reform mathematics education and I think that some of this reform is misguided, and this is in fact why I no longer work as an educational technologist. Without reforming work we as educators do to make links between the resources we use and the learning outcomes we hope to see borne out by children, there will be little effective change in the overall learning experiences for children.
Here is a paragraph from Dr. Ball’s article that stood out to me. For some context, Dr. Ball starts her article describing a student explaining how they understand odd versus even numbers. For further detail, I recommend reading her article.
Some teachers are convinced that manipulatives would have been the way to prevent the students’ “confusion” about odd and even numbers. This reaction makes sense in the current context of educational reform. In much of the talk about improving mathematics education, manipulatives have occupied a central place. Mathematics curricula are assessed by the extent to which manipulatives are used and how many “things” are provided to teachers who purchase the curriculum. Inservice workshops on manipulatives are offered, are usually popular, and well attended. Parents and teachers alike laud classrooms in which children use manipulatives, and Piaget is widely cited as having “shown” that young children need concrete experiences in order to learn…
Here is an updated paragraph with the current reform efforts focused on utilizing technology in mathematics education.
Some teachers are convinced that [technology] would have been the way to prevent the students’ “confusion” about odd and even numbers. This reaction makes sense in the current context of educational reform. In much of the talk about improving mathematics education, [the use of technology has] occupied a central place. Mathematics curricula are assessed by the extent to which [technology is] used and how many “things” are provided to teachers who purchase the curriculum. Inservice workshops on [technology] are offered, are usually popular, and well attended. Parents and teachers alike laud classrooms in which children use [technology], and [Papert] is widely cited as having “shown” that young children need [access to technology] in order to learn…
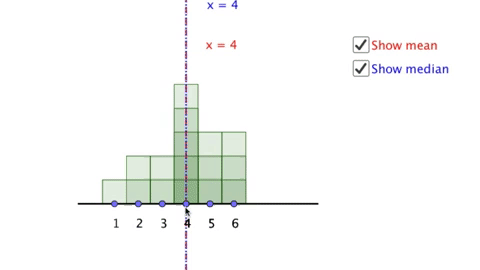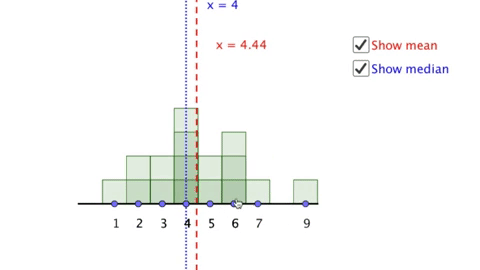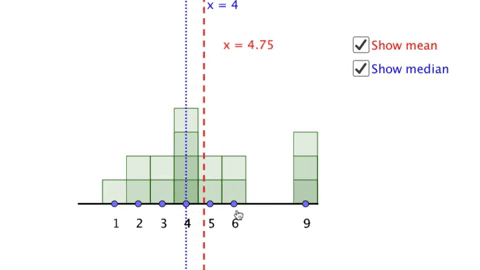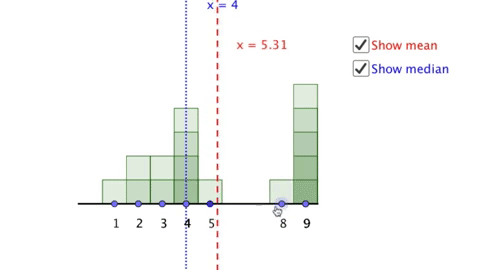
Here is an example of technology intended to be used in mathematics education. This is a virtual manipulative I created which is intended to draw students attention to how function rules can be represented as visual sequences. Try changing the sliders and keeping track of what you notice and what you wonder.
Now consider, what do you think children might notice when looking at this manipulative? What will they wonder? And most importantly, what will they learn as a result of using it?
If you have time, I recommend actually trying this activity out with a variety of children at different age levels. What I have learned is that children rarely see things the same things as adults (especially if those adults are mathematicians and/or mathematics teachers). In particular most children with whom I have used this particular manipulative do not attend to the differences between terms in the same way that adults do, and very few children even notice that the manipulative above includes an equation. They tend to focus almost entirely on the elements of the virtual manipulative over which they have control (the sliders) and the elements that change the most (the visual pattern) and in particular generally ignore features not immediately visible (the difference between terms) or recognizable (the equations).
Technology that relies on children independently making mathematical discoveries is likely to fail for some children. Given that one’s current mathematical knowledge is a large factor in how easily one makes mathematical discoveries, this use of technology may increase educational inequity rather than decrease it.
Recommendation: Utilize instructional strategies intended to make the sharing of mathematical ideas explicit for all students.
Here is another paragraph from Dr. Ball’s article:
Manipulatives –and the underlying notion that understanding comes through the fingertips– have become part of educational dogma: Using them helps students; not using them hinders students. There is little open, principled debate about the purposes of using manipulatives and their appropriate role in helping students learn…
Fortunately, there is tremendous debate about the use of technology in mathematics education, but most of this debate has centered on grain sizes of discussion that are far too broad to be helpful. Instead of questions like, “Is technology helpful in mathematics education?” we should be asking ourselves much more specific questions that have the same form as “is this use of this technology helpful for these students in this situation?” And then when we come up with a first draft answer for that question, we should make sure that our second draft includes some evidence from our students that the learning experience in question was actually improved by the use of the technology.
Recommendation: The links between what we hope children will learn from a particular activity and the evidence that they have learned should be made clear and investigated.
Here is another insightful quote from Dr. Ball:
My main concern about the enormous faith in the power of manipulatives, in their almost magical ability to enlighten, is that we will be misled into thinking that mathematical knowledge will automatically arise from their use. Would that it were so! Unfortunately, creating effective vehicles for learning mathematics requires more than just a catalog of promising manipulatives. The context in which any vehicle–concrete or pictorial–is used is as important as the material itself. By context, I mean the ways in which students work with the material, toward what purposes, with what kinds of talk and interaction. The creation of a shared learning context is a joint enterprise between teacher and students and evolves during the course of instruction. Developing this broader context is a crucial part of working with any manipulative. The manipulative itself cannot on its own carry the intended meanings and uses.
I sometimes see the same kind of thinking from mathematics educators (myself included); that just because a particular Desmos activity or Geogebra applet contains some mathematical idea, that children will learn the mathematical principles that are potentially generative in the activity. Sometimes some children see the mathematical principle, we have them present their work, and then we either hope or assume that this sample of children is representative of the whole class. Unfortunately, selection of students to present is a challenging activity that tends towards sharing strategies deemed as correct rather than surfacing a mathematical idea (like Sean’s observation in Deborah Loewenberg Ball’s article) that is fruitful to present and discuss even though an outside observer would consider the idea incorrect.
Recommendation: Before students engage in a technological activity, anticipate how we think they may consider the mathematical features. While students engage in a particular activity, listen to students talk, watch them work, and ask them questions to probe at their actual mathematical thinking. Use this information to potentially revise the activity.
Dr. Ball continues with this argument:
If we pin our hopes for the improvement of mathematics education on manipulatives, I predict that we will be sadly let down. Manipulatives alone cannot and should not–be expected to carry the burden of the many problems we face in improving mathematics education in this country. The vision of reform in mathematics teaching and learning encompasses not just questions of the materials we use but of the very curriculum we choose to teach, in what ways, to whom, and in what kinds of classroom environments and discourse. It centers on new notions about what counts as worthwhile mathematical knowledge. These issues are numerous and complex. For instance, we need to shift from an emphasis on computational proficiency to an emphasis on meaning and estimation, from an emphasis on individual practice to an emphasis on discussion and on ideas, reasoning, and solution strategies. We need to alter the balance of the elementary curriculum from a dominant focus on numbers and operations to a broader range of mathematical topics, such as probability and geometry. We need to shift from a cut-and-dried, right-answer orientation to one that supports and encourages multiple modes of representation, exploration, and expression. We need to increase the participation, enthusiasm, and success of a much wider range of students. Manipulatives undoubtedly have a role to play in these aims, by enhancing the modes of learning and communication available to our students. But simply getting manipulatives into every elementary classroom cannot possibly suffice to fulfill these aims.
This leads to some questions that we educators can ask ourselves before we embark on using some new technology with students (in the same way that at the time of Deborah Loewenberg Ball’s article was published that manipulatives were a new technology for many teachers).
- Does using this technology help my students learn mathematics that they can use without the use of this technology?
- How will someone who does not yet know the mathematics embedded within this technological tool see the mathematics?
- Does this technology focus solely on the acquisition of a limited set of mathematical knowledge or is it possible for students to use deliberate practice to identify patterns across different problems and acquire new mathematical ideas?
- Does this technology make it harder for my students to interact with each other and with me?
- How will I learn how my students understand the mathematical ideas that are the focus of this lesson?
- Who is the audience of this technology?
- Does this technology exacerbate existing inequities in mathematics education?
Some of these questions were originally in this post.
I don’t have answers to all of these questions unfortunately but I think as a community of mathematics educators, we should be at least trying to answer them. I also have not unpacked some really large scale and potentially damaging initiatives around online learning and personalized learning. Stay tuned for a Part 2 to this post focused more on these uses of technology.