
Is this curriculum?
On the day before I first started teaching, the district coordinator came to me and handed me a piece of paper with twenty questions on it. “Here’s what you have to teach, David. If your students can answer all twenty of these questions by the end of the year, you will be fine.”
Needless to say that this was insufficient curriculum. But what kind of curriculum would have been useful for me at that stage in my career?
A place many math educators, especially in our accountability-driven system, seem to start when teaching mathematics is teaching children how to solve questions. “Here’s how you solve this kind of question.” The connections between different problems are left for students to discover on their own.
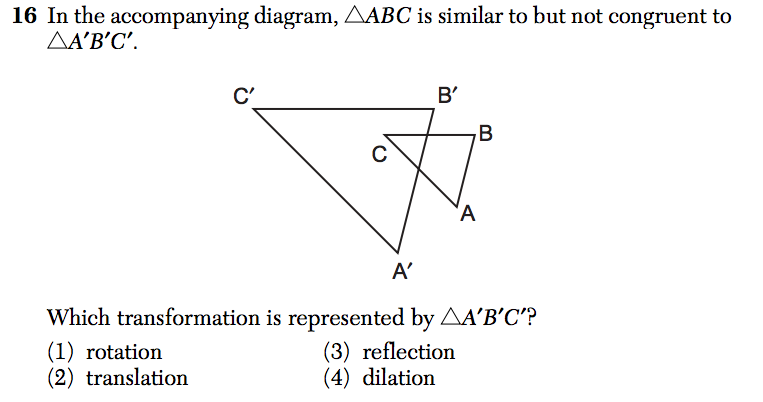
Strategy: If the triangles are a different size, the transformation is a dilation.
The advantage to this system is that you can look at the state assessment and check off of all of the question types and feel like you have done your job. For the old NY state exam, this approach works in the sense that students were able to sit down at the exam and feel like they had been prepared for every question since the assessment was so predictable, even if they didn’t always know how to solve the problems .
The problem with this approach is that students now have to remember each question archetype and each solution to each type of problem separately, leading to a relatively unorganized and overwhelming set of problem-solving schema for students. This leads to students forgetting how to solve individual problems, forgetting which solution strategy they should use when, or misapplying strategies to solve problems for which the strategy is not appropriate. Even when students do master all of the problem types, knowing how to solve problem x, y, or z doesn’t help students make connections when they start studying further areas of mathematics.
To their credit, every textbook author I’ve ever read takes a different approach (to some degree). Textbooks start by dividing the year’s worth of mathematics to be learned into units of study and apportioning mathematical principles into those units. Within each unit of study, specific problems are used to illuminate mathematical ideas and ideally students at the end of a unit can articulate the mathematical ideas they have learned, rather than just the problems to which they apply. Where textbooks often fall down is in making the connections between units and ideas explicit.
When well done, problems become vehicles for teaching mathematical principles. Mathematical representations (like graphs, tables, etc…) are embedded across the units so that students get multiple exposures to these critical representations and can use them to make sense of similarities and differences between different mathematical ideas. Ideally students explicitly learn connections between different mathematical ideas so that they see, for example, how solving a linear equation is related to solving a quadratic equation and how the graph of an absolute function is related to the graph of a linear function.
One way to support students in making these connections is to ask them to answer reflection questions like: How is what we learned today related to what we learned yesterday? How is this problem we solved today like the problems we solved last week? What did we learn today that we can probably generalize and use to solve other problems? At the very least while planning, make sure you can answer these questions yourself.
A major disadvantage of the second approach to teaching mathematics is that it takes much more work to organize curricular resources into the general themes and to make the connections between ideas explicit. Rare is the classroom teacher who has time to do this all herself. This is one of the reasons why I think well-organized curriculum of some kind is always going to be a helpful resource.
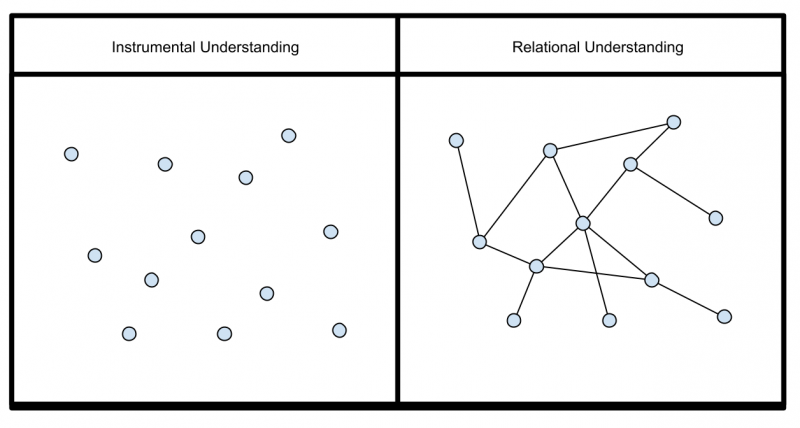
There is a gradient between the two approaches to teaching mathematics.
For further reading on a related topic, check out this post on instrumental versus relational knowledge.

Xavier B. (@somenxavier) says:
Absolutely I agree with you. The problem is how to design your application of the curricula for doing this.
Just solving problems leads to a trouble: how to introduce other ways of solving problems. Almost 100% of the problems in Maths could be solved with proportionality. So how to introduce equations? for example
February 7, 2016 — 9:37 am
Carmel Schettino says:
Such a great post, David – thanks for sharing this. To me, it’s the biggest difference between PBL and what I’ve called Relational PBL. I don’t know if read a lot about relational pedagogy, but it is the key to allowing students to focus on the relationships between the content and the community in the classroom. Excellent posts and it’s great to hear someone of your expertise talking about it!
February 7, 2016 — 3:31 pm
Gary Davis says:
David, very nice discussion of an important issue. Have to say I find word problems like #1 somewhat ridiculous – only in math class would we do this: most people would just ask Jamie how old she was!
Q 3 seemed more meaningful
February 12, 2016 — 2:27 pm
David Wees says:
Hi Gary,
Yeah, that is a different point than I am making but an equally valid one. There’s no point in making this a problem about ages, you might as well strip the context because it actually interferes with thinking about the numerical relationships because as you said, no one ever thinks about age relationships like this question suggests.
As for question 3, I asked and answered a very similar question many times as a student, but in my case I was interested in what score I needed on the upcoming test to get an A.
Thanks for commenting.
February 12, 2016 — 2:38 pm
David Wees says:
Hi Carmel,
I have not heard it called ‘relational pedagogy’ but I kind of like the phrase. It captures both the idea that students are working toward common goals together and that we should work to build their community in doing this AND that teaching is about helping kids find and articulate relationships between different ideas, rather than teaching individual ideas in isolation.
David
February 12, 2016 — 2:40 pm
David Wees says:
Hi Xavier,
I find Dan Meyer’s posts on intellectual need to be a helpful framework for thinking about generate a need for a different type of mathematics.
Yes, you can solve many problems by thinking about the relationships between numbers and trying out different values that satisfy the relationships you can identify and see if they work to satisfy other constraints of the problem, but this quickly becomes time consuming and tedious for some problems, making other types of mathematics more useful to know.
David
February 12, 2016 — 2:42 pm
J Guadagni says:
I am in the process of creating a 9th grade MathLab to supplement my daily Algebra I class. 2 days a week 80 mins each. My goal is to teach problem solving, critical thinking, and perseverance. It will be PBL and it will push the envelope. I’m looking for resources that outline characteristic, qualities, and strategies of a good problem solver. Our kids give up too easily as soon as they see a problem that we haven’t covered in class, especially on the standardized test. Thank you ahead of time. Please follow my journey and contribute on Twitter @MrGuads. Blog to come shortly.
February 12, 2016 — 6:42 pm
David Wees says:
Hi Justin,
I recommend checking out these instructional activities we’ve been using in our project. I’d start with using Contemplate then Calculate several times with students (maybe 5 or 6 times in a two week time period) until you and your students feel really comfortable with the routine and then you can try it a little less frequently after that (maybe 1 or 2 times a week) or keep using it fairly frequently. After at least a month or so, you can try introducing Connecting Representations.
Examples and descriptions of both instructional activities can be found at the link above.
David
February 12, 2016 — 7:01 pm
Peter Smyth says:
A great question is at what grade level can we get this kind of teaching in place. I generally seem to hear mostly high school teachers talking the talk, but woebetide them when trying to change the inertia of students (and their parents)who arrive after eight or so years of instrumental learning.
February 13, 2016 — 11:57 am
Samantha Malaquias says:
Also going off of Peter’s comment, it is hard to transition from one form of teaching to another. Once a student learns to do thing one way, they do not necessarily want to learn a different way.
April 25, 2016 — 2:17 am
Robyn Matus says:
Hi David,
Great post, really helpful for textbook publishers (like us).
Hearing educator’s thoughts on how to make the connection between units and ideas explicit in problem solving is very important. This sort of information you share is so helpful to us developing better learning material.
Thanks for your insights.
Robyn Matus
ContinentalPress.com
September 30, 2016 — 1:40 pm
David Wees says:
Hey Robyn,
Thank you! You might also find this post I wrote on Ambitious Mathematics Curriculum useful then.
David
September 30, 2016 — 3:07 pm