This diagram represents a problem in education which is, by no means, the ONLY problem in education.
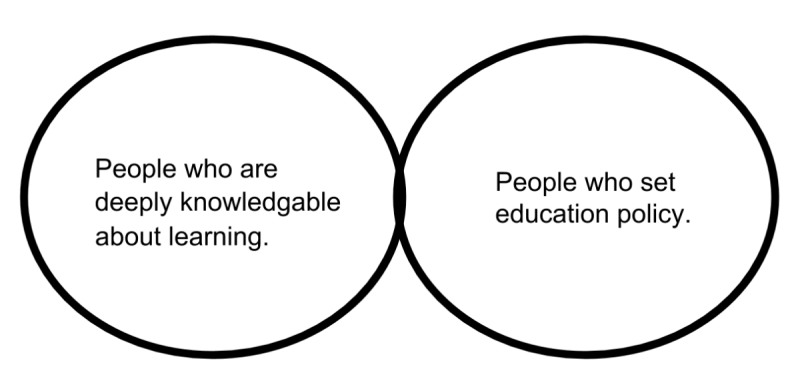
How do we change this paradigm?
Education ∪ Math ∪ Technology
This diagram represents a problem in education which is, by no means, the ONLY problem in education.

How do we change this paradigm?
This is part two of a three part series on formative assessment. This post deals with some things you can do between individual lessons based on formative assessment and during a lesson. You can read part one here.
Introduction
The objective of this post is to describe two possible procedures teachers can use for ongoing, day-to-day formative assessment. The first of these procedures is easier to implement, but gives teachers less information on what students understand. Remember that a primary objective of formative assessment is to create a feedback loop for both teachers and students into the teaching and learning process.
Example 1
At the end of your last class you gave an exit slip. One strategy, which is not too time-consuming, is to take the exit slip and first sort it into No/Yes piles, and then sort these piles into 3-4 solution pathway piles, essentially organizing all of the student work by whether or not it is correct and what strategy students used. It may be useful to have an other group, with students whose strategy which are unable to decode.
These groups of student can be used to decide on student groups (recommendation: group by different strategy) for the following day, decide if you need to try a different strategy for tomorrow, and/or find examples of student work to present to students. It can also be used to decide on re-engagement strategies1 for the lesson from the previous day, or just decide that you can move onto the next topic in your unit sequence.
Example 2
Part of my current role is to help teachers use formative assessment in their teaching. This has turned out to have some interesting challenges, and has helped me grow tremendously as a teacher.
Dylan Wiliam and Paul Black define formative assessment as “as encompassing all those activities undertaken by teachers, and/or their students, which provide information to be used as feedback to modify [emphasis mine] the teaching and learning activities in which they are engaged.” (Black and Wiliam, 1998a, p7)1 Another definition I have used is, “A formative assessment or assignment is a tool teachers use to give feedback to students and/or guide their instruction.” Black and Wiliam’s definition is superior because it includes the important “what next” aspect of formative assessment. If the purpose of education is to cause change in a student, formative assessment is the tool that is used to measure and adjust the direction of that change.
My observation is that it depends on how the information collected by teachers is used that ensures if the assessment is formative in nature or not; assessment information not acted on is not formative in nature. The two challenges I have observed in the use of formative assessment are knowing how to act on the information gathered, and being able to find (in an unbiased way) evidence that student thinking has changed based on our instruction.
First, information collected from students can come in a variety of ways. There is the more formal written formative assessment information a teacher can collect, for example: a quiz, an exit slip, a homework assignment, a project, etc… There is also the less formal formative assessment information a teacher can collect (aside: I recommend a clipboard and using a template for quickly recording this kind of information), for example: which students raised their hands to answer a question, how able is a student to explain their reasoning, how does a student respond to another student’s thinking, etc… Each assessment type has its advantages and disadvantages. Formal, written assessment has the advantage that a teacher can look at and think about it when they have time outside of the classroom. The informal assessments have the advantage that a teacher can listen to, make sense of, immediately clarify, and make use of the information.
There are three main ways teachers can effectively respond to assessment information from students.
It is most challenging to use formative assessment information immediately, and least challenging to use it to guide an overall unit plan. It is probably worth looking at these opportunities to respond from the most general response, to the most specific.
Formative assessment at the unit level
Imagine you have given a pre-assessment to your students on their knowledge of, and the ability to apply, the Pythagorean theorem to solve for missing lengths in right triangle problems. You discover that the distribution of results for 30 students on the pre-assessment looks something like this, where 4 is given as the cut score2.

Remembering that this assessment is at best a proxy for what students have learned3, what do you do? You can see from the distribution of scores that most students did not achieve the cut-score for the task. The situation is more complex however, because a significant percentage of the students did!
You could teach a mini-unit on this topic with the intention of reviewing the material in more depth for students who reached the cut-score for the assessment, and to teach the material as new for students who did not. This is problematic because many students will feel they know the content, and a common reaction to when teachers teach material that students have been told about before (but not necessarily learned) is that students tune out.
If you do choose to teach a mini-unit, you could monitor progress of all students during it. This will help direct your unit toward the most important sub-skills of the unit, and not cover tasks that students are already fairly able to do. For example, if students are all able to consistently apply the Pythagorean theorem to find the hypotenuse of a right triangle, further explicit instruction in this area is not necessary, but it could be a good way to start a task in order to build on strength.
You could also use re-engagement as an alternative to reteaching. This will allow the students who almost meet the proficiency level for this standard a chance to revisit the work that they did and reflect on it and compare their work with other students. All of your students will hopefully increase their understanding of the focus content during re-engagement, but a potential drawback is that not all of them will necessarily improve their mental models to meet our required proficiency level.
You can also use tasks that target the weaknesses of students (or alternatively build upon their strengths) while still allowing all of your students a chance to grow. A task that has a low entry to accessing the task, but has a high ceiling can be an excellent way to differentiate instruction without having to do a huge amount of planning. This also gives students with more background knowledge a chance to deepen their knowledge by thinking about and discussing other people’s misconceptions. During these tasks, it is also possible to confer with individual students and give targeted support to them.
You could return the work to students but give feedback questions instead of scores on the work itself. This way all students, including those that “mastered” the standard have something to work toward. The research suggests that written comments on student work, without numerical grades, are best to produce the desired outcome in students, which is to reflect on their work.
Remember in your unit planning that every time you decide that “enough students get it, and that it is time to move on”, if this concept is critical to understanding future concepts, you’ve left some students with no support. You should plan to find ways to allow students to re-engage with prior concepts and be able to move forward with the rest of the group. You could, for example, spiral back to previous topics through-out the year (which is good practice for all students).
The overall point you should take away from this section is that formative assessment can, and should, be used to modify (or at least justify) your unit plan. If your unit plan is a map through a section of mathematical territory, formative assessment is a bit like your GPS.
In part two of this post, I will outline some examples of day to day formative assessment.
What other suggestions do you have for teachers who are looking to embed formative assessment in their unit planning process?
Information:
1. Black, P.J., & Wiliam, D. (1998a). Assessment and classroom learning. Assessment in Education: Principles, Policy & Practice
2. A cut-score refers to a score which is used in standards-based assessment that indicates what level students need to reach on a performance task to be considered proficient in the associated standard.
3. All assessment can best measure is a subset of what students are able to do, based on the knowledge and skills they have constructed in their heads. Therefore, all assessments are proxies for what students know. A student who achieves 100% on an assessment does not necessarily understand how to apply a concept 100% of the time, you are best able to say that they were able, on this day, at this time, to write down scribblings we call language which matched your expectations of what those scribblings should look like. This is relevant because you may sometimes find examples of contradictory information, where a student appears on one task to have mastered a standard, and yet appears on another assessment to have not mastered the standard. It also suggests that we can only make the claim that a student has mastered a standard if they have demonstrated proficiency in at least a few contexts.
4. For other examples of formative assessment, see this presentation that I curated. It has 54 different possible formative assessment strategies in it, some of which are more appropriate for a class focused on literacy skills, and some of which are useful for a mathematics classroom.
Here are seven questions my son asked today.
Kids are scientists. My job with my son is to teach how to answer his own questions.
A few days ago, my wife told my son that he should do some mathematics from a 2nd grade workbook we had, and told him he could choose what he worked on. My son opened up the book to near the end of the workbook and decided to try some 2 digit subtraction exercises.
Here is an example of his work.
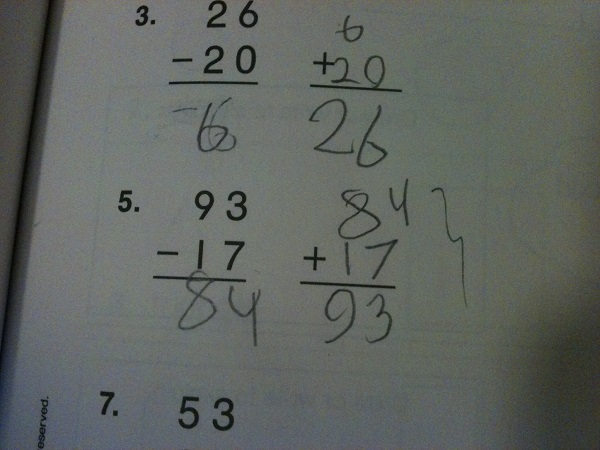
As I often do, I sat down with him and asked him to explain his work (note: I do this whether or not the work is correct). He told me, “Okay. Ninety take-away ten is eighty and seven take-away three is four, so the answer is …” and then he paused, “Okay. Mommy is right the answer is seventy-six.” I asked him why he changed his answer, but he was not able to articulate what made him change his mind.
We talked next about possible strategies we could use to solve this problem.
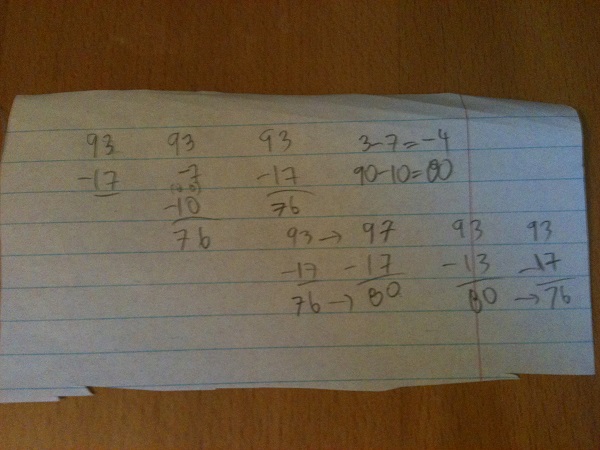
My son said that one way to find the answer would be to subtract seven from ninety-three, which would give eighty-six, and then subtract ten more, which would result in seventy-six. Another strategy he said he could use would be to take seven away from three first, which is negative four. Ten subtracted from ninety would be eighty, and eighty plus negative four would also be seventy-six. I suggested that another strategy could be to change ninety-three to ninety-seven, noting that this should increase the answer to our subtraction by four. Next we would subtract seventeen from ninety-seven, which my son said, “Obviously 97 take-away 17 is 80.” Finally, we need to reduce our answer of 80 by 4, to get a final answer of 76.
You may notice that I have not yet introduced the standard subtraction algorithm that includes borrowing a ten from the ninety, and then doing the subtraction as eighty take-away ten, and thirteen take-away seven is six, leading to a final answer of seventy-six as well. This is because I want to make sure that my son has a good understanding of how subtraction works first, so that I do not end up confusing him with what might other-wise feel like an arbitrary procedure.
Teaching is a learned activity. As such, the act of teaching requires that the teacher have a mental model of what it means to teach. When teachers teach in ways which appear to an outside observer to be ineffective or poorly thought-out, it is because they are using a flawed model for understanding teaching and learning. Blaming teachers for having flawed models is like blaming students for not knowing things; it doesn’t solve the problem, it may even exacerbate it.
Teaching is also incredibly complex. Once a teacher starts teaching, it can take ten years before they begin to plateau in terms of their expertise. Unfortunately, most educators work towards improving their practice in isolation, and receive little direct feedback on their work. Many of the colleagues I have taught with over the years have never received formal feedback on their teaching! Often the feedback educators do receive is inconsistent, haphazard, and hard to utilize. The best feedback most educators currently get about the effectiveness of their work is the direct impact it has on student learning in their classroom.
If we want to improve education, aside from continue to work on issues of inequity and division in our society, we must plan schools so that teachers are given more time to collaborate and plan their work together. We must also build in an expectation that the job of teaching includes the job of learning more about teaching, and that constructive feedback about one’s work is the norm, rather than an oddity. We must embed learning about teaching into what it means to be a teacher.
The following are studies which were all featured in the media in 2013. I am posting them here in the hope that they will be read more widely than they are, and that educators will examine the research themselves, and think about how this may affect their current practice.
I’ve included a link to the study as well as either an abstract or the summary of the research as presented by the author of the article linked. These are all studies which either support current hypothesises about the importance of recognizing social and cultural issues in teaching and learning mathematics, relate to the importance of early mathematics education (and the role parents can play), or observe that the style of instruction that is used has an impact on student learning.
Finally, I’ve included a couple of studies I read which were not specifically done in the area of mathematics education itself, but which I think are obviously related.
Socio-emotional and cultural issues
“This study draws upon social cognitive career theory and higher education literature to test a conceptual framework for understanding the entrance into science, technology, engineering, and mathematics (STEM) majors by recent high school graduates attending 4-year institutions. Results suggest that choosing a STEM major is directly influenced by intent to major in STEM, high school math achievement, and initial postsecondary experiences, such as academic interaction and financial aid receipt. Exerting the largest impact on STEM entrance, intent to major in STEM is directly affected by 12th-grade math achievement, exposure to math and science courses, and math self-efficacy beliefs—all three subject to the influence of early achieve- ment in and attitudes toward math. Multiple-group structural equation modeling analyses indicated heterogeneous effects of math achievement and exposure to math and science across racial groups, with their positive impact on STEM intent accruing most to White students and least to under- represented minority students.”
Women do better on math tests when they fake their names
“Unsurprisingly, and as the title of this post already suggests, women do indeed perform better on math tests when they assume a name other than their own — and this happens regardless of whether they take a male or female name.
As a recent study by Shen Zhang has shown, using another person’s name is a kind of hack to overrule the self-reputational threat — the fear some women have of doing poorly when they’re concerned that it’ll be taken as proof of a stereotype. But removing this pressure seems to alleviate the fear and the distraction.
For the study, Zhang recruited 110 women and 72 men — all of them undergrads — and had them answer 30 multiple-choice math questions. Prior to the test, and in an effort to instill the stereotype threat, all participants were told that men typically outperform women at math. Some of the volunteers were told to write the test under their real name, but some were told to complete the test under one of four different aliases, either Jacob Tyler, Scott Lyons, Jessica Peterson, or Kaitlyn Woods…”
Early Nervousness Over Number Impacts Future Performance
“According to a recent study by Rose Vukovic, NYU Steinhardt professor of teaching and learning, math gives some New York City students stomachaches, headaches, and a quickened heartbeat. In short, math makes these children anxious.
“Math anxiety hasn’t really been looked at in children in early elementary grades,” said Vukovic, a school psychologist and researcher of learning disabilities in mathematics. “The general consensus is that math anxiety doesn’t affect children much before fourth grade. My research indicates that math anxiety does in fact affect children as early as first grade.”
Vukovic’s first study, “Mathematics Anxiety in Young Children,” will be published in the Journal of Experimental Education. It explored mathematics anxiety in a sample of ethnically and linguistically diverse first graders in New York City Title I schools. Vukovic and her colleagues found that many first grade students do experience negative feelings and worry related to math. This math anxiety negatively affects their math performance when it comes to solving math problems in standard arithmetic notation…”
Female teachers’ math anxiety affects girls’ math achievement
“People’s fear and anxiety about doing math—over and above actual math ability—can be an impediment to their math achievement. We show that when the math-anxious individuals are female elementary school teachers, their math anxiety carries negative consequences for the math achievement of their female students. Early elementary school teachers in the United States are almost exclusively female (>90%), and we provide evidence that these female teachers’ anxieties relate to girls’ math achievement via girls’ beliefs about who is good at math. First- and second-grade female teachers completed measures of math anxiety. The math achievement of the students in these teachers’ classrooms was also assessed. There was no relation between a teacher’s math anxiety and her students’ math achievement at the beginning of the school year. By the school year’s end, however, the more anxious teachers were about math, the more likely girls (but not boys) were to endorse the commonly held stereotype that “boys are good at math, and girls are good at reading” and the lower these girls’ math achievement. Indeed, by the end of the school year, girls who endorsed this stereotype had significantly worse math achievement than girls who did not and than boys overall. In early elementary school, where the teachers are almost all female, teachers’ math anxiety carries consequences for girls’ math achievement by influencing girls’ beliefs about who is good at math.”
Early learning and parental involvement
“This study focuses on three main goals: First, 3-year-olds’ spatial assembly skills are probed using interlocking block constructions (N = 102). A detailed scoring scheme provides insight into early spatial processing and offers information beyond a basic accuracy score. Second, the relation of spatial assembly to early mathemati- cal skills was evaluated. Spatial skill independently predicted a significant amount of the variability in concur- rent mathematical performance. Finally, the relationship between spatial assembly skill and socioeconomic status (SES), gender, and parent-reported spatial language was examined. While children’s performance did not differ by gender, lower-SES children were already lagging behind higher-SES children in block assembly. Furthermore, lower-SES parents reported using significantly fewer spatial words with their children.”
What’s the earliest age that children think abstractly?
“Caren Walker and Alison Gopnik (2013) examined toddlers ability to understand a higher order relation, namely, causality triggered by the concept “same.”
The experimental paradigm worked like this. The toddler was shown a white box and told “some things make my toy play music and some things do not make my toy play music.” The child then observed three pairs of blocks that made the box play music, as shown below. On the fourth trial, the experimenter put one block on the box and asked the child to select another that would make the toy play music. There were three choices: a block that looked the same as the one already on the toy, a block that had previously been part of a pair that made the toy play music, and a completely novel block…”
Quality of early parent input predicts child vocabulary 3 years later
“Children vary greatly in the number of words they know when they enter school, a major factor influencing subsequent school and workplace success. This variability is partially explained by the differential quantity of parental speech to preschoolers. However, the contexts in which young learners hear new words are also likely to vary in referential transparency; that is, in how clearly word meaning can be inferred from the immediate extralinguistic context, an aspect of input quality. To examine this aspect, we asked 218 adult participants to guess 50 parents’ words from (muted) videos of their interactions with their 14- to 18-mo-old children. We found systematic differences in how easily individual parents’ words could be identified purely from this socio-visual context. Differences in this kind of input quality correlated with the size of the children’s vocabulary 3 y later, even after controlling for differences in input quantity. Although input quantity differed as a function of socioeconomic status, input quality (as here mea- sured) did not, suggesting that the quality of nonverbal cues to word meaning that parents offer to their children is an individual matter, widely distributed across the population of parents.”
What counts in the development of young children’s number knowledge?
“Prior studies indicate that children vary widely in their mathematical knowledge by the time they enter preschool and that this variation predicts levels of achievement in elementary school. In a longitudinal study of a diverse sample of 44 preschool children, we examined the extent to which their understanding of the cardinal meanings of the number words (e.g., knowing that the word “four” refers to sets with 4 items) is predicted by the “number talk” they hear from their primary caregiver in the early home environment. Results from 5 visits showed substantial variation in parents’ number talk to children between the ages of 14 and 30 months. Moreover, this variation predicted children’s knowledge of the cardinal meanings of number words at 46 months, even when socioeconomic status and other measures of parent and child talk were controlled. These findings suggest that encouraging parents to talk about number with their toddlers, and providing them with effective ways to do so, may positively impact children’s school achievement…”
“Do individual differences in the brain mechanisms for arithmetic underlie variability in high school mathematical competence? Using functional magnetic resonance imaging, we correlated brain responses to single digit calculation with standard scores on the Preliminary Scholastic Aptitude Test (PSAT) math subtest in high school seniors. PSAT math scores, while controlling for PSAT Critical Reading scores, correlated positively with calculation activation in the left supramarginal gyrus and bilateral anterior cingulate cortex, brain regions known to be engaged during arithmetic fact retrieval. At the same time, greater activation in the right intraparietal sulcus during calculation, a region established to be involved in numerical quantity processing, was related to lower PSAT math scores. These data reveal that the relative engagement of brain mechanisms associated with procedural versus memory-based calculation of single-digit arithmetic problems is related to high school level mathematical competence, highlighting the fundamental role that mental arithmetic fluency plays in the acquisition of higher-level mathematical competence.”
Young Children’s Interpretation of Multi-Digit Number Names: From Emerging Competence to Mastery
“This study assessed whether 207 3- to 7-year-olds could interpret multi-digit numerals using simple identification and comparison tasks. Contrary to the view that young children do not understand place value, even 3-year-olds demonstrated some competence on these tasks. Ceiling was reached by first grade. When training was provided (based on either base-10 blocks or written symbols), there were significant gains, suggesting that children can improve their partial understandings with input. Our findings add to what is known about the processes of symbolic development and the incidental learning that occurs prior to schooling, as well as specifying more precisely what place value misconceptions remain as children enter the educational system.”
Instructional strategies
Study shows new teaching method improves math skills, closes gender gap in young students
“When early elementary math teachers ask students to explain their problem-solving strategies and then tailor instruction to address specific gaps in their understanding, students learn significantly more than those taught using a more traditional approach. This was the conclusion of a yearlong study of nearly 5,000 kindergarten and first-grade students conducted by researchers at Florida State University.
The researchers found that “formative assessment,” or the use of ongoing evaluation of student understanding to inform targeted instruction, increased students’ mastery of foundational math concepts that are known to be essential to later achievement in mathematics and science…”
Academic music: music instruction to engage third-grade students in learning basic fraction concepts
“This study examined the effects of an academic music intervention on conceptual understanding of music notation, fraction symbols, fraction size, and equivalency of third graders from a multicultural, mixed socio-economic public school setting. Students (N = 67) were assigned by class to their general education mathematics program or to receive academic music instruction two times/week, 45 min/session, for 6 weeks. Academic music students used their conceptual understanding of music and fraction concepts to inform their solutions to fraction computation problems. Linear regression and t tests revealed statistically significant differences between experimental and comparison students’ music and fraction concepts, and fraction computation at posttest with large effect sizes. Students who came to instruction with less fraction knowledge responded well to instruction and produced posttest scores similar to their higher achieving peers.”
Non-traditional mathematics curriculum results in higher standardized test scores, study finds
“James Tarr, a professor in the MU College of Education, and Doug Grouws, a professor emeritus from MU, studied more than 3,000 high school students around the country to determine whether there is a difference in achievement when students study from an integrated mathematics program or a more traditional curriculum. Integrated mathematics is a curriculum that combines several mathematic topics, such as algebra, geometry and statistics, into single courses. Many countries that currently perform higher than the U.S. in mathematics achievement use a more integrated curriculum. Traditional U.S. mathematics curricula typically organize the content into year-long courses, so that a 9th grade student may take Algebra I, followed by Geometry, followed by Algebra II before a pre-Calculus course.
Tarr and Grouws found that students who studied from an integrated mathematics program scored significantly higher on standardized tests administered to all participating students, after controlling for many teacher and student attributes. Tarr says these findings may challenge some long-standing views on mathematics education in the U.S…”
Duke Study Finds Improving ‘Guesstimating’ Can Sharpen Math Skills
“You may not have heard of it, but it’s a skill you probably use everyday, like when choosing the shortest line at the grocery store or the toll booth with the fewest number of cars. Approximate number math, or ‘guesstimating,’ is the ability to instinctively estimate quantities without counting. Researchers at Duke University set out to discover whether practicing this ability would improve symbolic math skills, like addition and subtraction.
They discovered that study participants who were given approximate number training sessions did dramatically better on symbolic math tests than those who were not. Those who received training also received significantly higher scores on the math tests after the training than before…”
Related research
What Science Teachers Need to Know
“The researchers (Sadler et al., 2013) tested 181 7th and 8th grade science teachers for their knowledge of physical science in fall, mid-year, and years end. They also tested their students (about 9,500) with the exact same instrument.
Each was a twenty-item multiple choice test. For 12 of the items, the wrong answers tapped a common misconception that previous research showed middle-schoolers often hold. For example, one common misconception is that burning produces no invisible gases. This question tapped that idea:
But the researchers didn’t just ask the teachers to pick the right answer. They also asked teachers to pick the answer that they thought their students would pick…”
Research: Improving Test Scores Doesn’t Equate to Improving Abstract Reasoning
“A team of neuroscientists at MIT and other institutions has found that even when schools take instructional steps that help raise student scores on high-stakes tests, that influence doesn’t translate to improvements in learners’ abilities to perform abstract reasoning. The research, which took place a couple of years ago, studied 1,367 then-eighth-graders who attended traditional, charter, and exam schools in Boston. (All were public schools.)
The researchers found that while some schools raised their students’ scores on the Massachusetts Comprehensive Assessment System (MCAS) — a sign of “crystallized intelligence” — the same efforts don’t result in comparable gains in “fluid intelligence.” The former refers to the knowledge and skills students acquire in school; the latter describes the ability to analyze abstract problems and think logically…”
Classes should do hands-on exercises before reading and video, Stanford researchers say
“A new study from the Stanford Graduate School of Education flips upside down the notion that students learn best by first independently reading texts or watching online videos before coming to class to engage in hands-on projects. Studying a particular lesson, the Stanford researchers showed that when the order was reversed, students’ performances improved substantially.
While the study has broad implications about how best to employ interactive learning technologies, it also focuses specifically on the teaching of neuroscience and underscores the effectiveness of a new interactive tabletop learning environment, called BrainExplorer, which was developed by Stanford GSE researchers to enhance neuroscience instruction…”