A few days ago, my wife told my son that he should do some mathematics from a 2nd grade workbook we had, and told him he could choose what he worked on. My son opened up the book to near the end of the workbook and decided to try some 2 digit subtraction exercises.
Here is an example of his work.
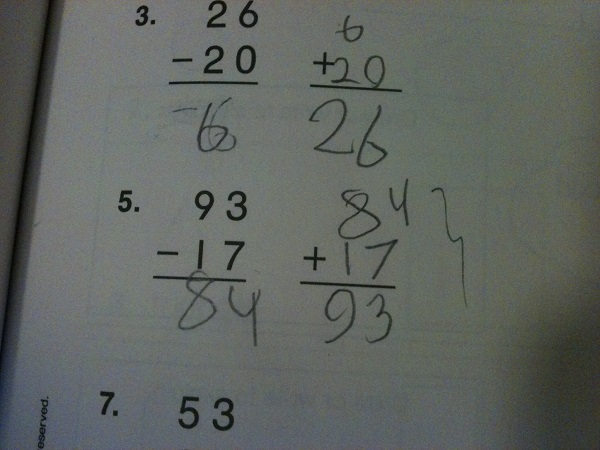
As I often do, I sat down with him and asked him to explain his work (note: I do this whether or not the work is correct). He told me, “Okay. Ninety take-away ten is eighty and seven take-away three is four, so the answer is …” and then he paused, “Okay. Mommy is right the answer is seventy-six.” I asked him why he changed his answer, but he was not able to articulate what made him change his mind.
We talked next about possible strategies we could use to solve this problem.
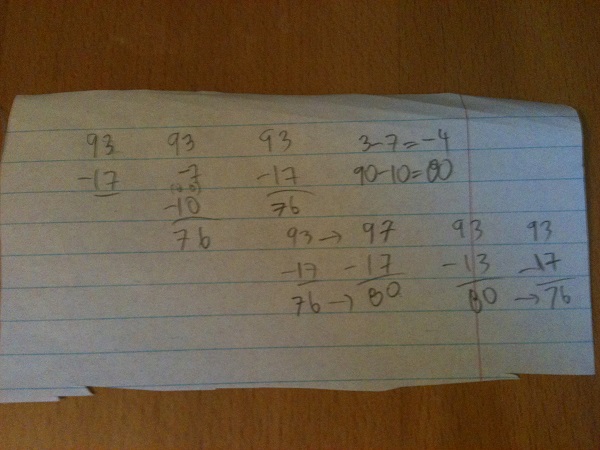
My son said that one way to find the answer would be to subtract seven from ninety-three, which would give eighty-six, and then subtract ten more, which would result in seventy-six. Another strategy he said he could use would be to take seven away from three first, which is negative four. Ten subtracted from ninety would be eighty, and eighty plus negative four would also be seventy-six. I suggested that another strategy could be to change ninety-three to ninety-seven, noting that this should increase the answer to our subtraction by four. Next we would subtract seventeen from ninety-seven, which my son said, “Obviously 97 take-away 17 is 80.” Finally, we need to reduce our answer of 80 by 4, to get a final answer of 76.
You may notice that I have not yet introduced the standard subtraction algorithm that includes borrowing a ten from the ninety, and then doing the subtraction as eighty take-away ten, and thirteen take-away seven is six, leading to a final answer of seventy-six as well. This is because I want to make sure that my son has a good understanding of how subtraction works first, so that I do not end up confusing him with what might other-wise feel like an arbitrary procedure.