Tonight my wife asked me why 4 – (-3) = 7. Apparently my son had "explained" it to her earlier tonight, but she hadn’t really understood his explanation. So I gave it a shot.
First I tried the same explanation that seemed to work for my son when he asked me what 4 – (-3) would be earlier today.
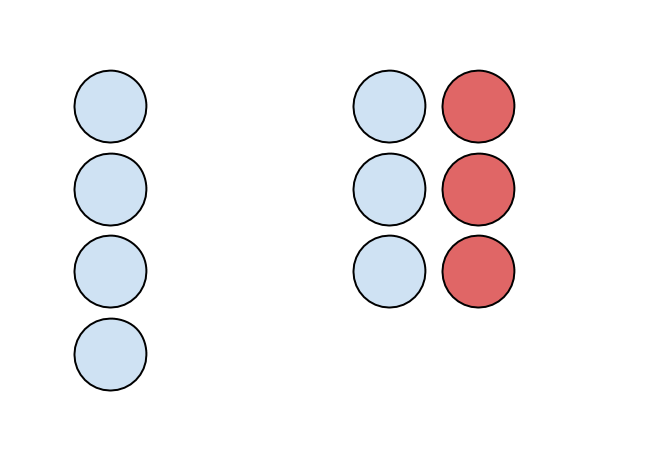
Me: "Imagine you had 4 blue circles, representing 4 positive 1s or 4 total. To this you add 1 positive circle and one negative circle. What would be the new total?"
My wife: "Still four. You added 0."
Me: "Okay, so let’s add 0 like this 3 times so the total will still be 4, right?"
My wife: "I get it. I don’t know why we are doing this, but okay."
Me: "So now, I take away the three negative circles, and therefore I am taking away a total of negative three from this picture and I’m left with 7. Therefore 4 – (-3) = 7."
My wife: "I don’t get it."
I tried a number line representation.

My wife: "I like looking at things on the number line."
Me: "Now imagine I’m on the number line at 4. If I subtracted 3, I’d end up at 1, so if I subtract -3, I must do the opposite, and so I end up at 7."
My wife: "I don’t get it."
Next, I tried operation consistency.

Me: "Okay, let’s try again. You agree that 4 + -3 = 1, right?"
My wife: "Yes. I understand that."
Me: "And 4 + 3 = 7 is obvious to you, as is 4 – 3 = 1. 4 – (-3) can’t be the same as 4 – 3, so it must be that 4 – (-3) = 7."
My wife: "That makes no sense."
I tried going back to the number line.

Me: "Okay, so what’s the distance between 5 and 2 on the number line?"
My wife: "3."
Me: "Right, since 5 – 2 is 3. Basically, one way to think of subtraction is that it gives you the distance between two points on the number line."
My wife: "Aaaaaah, I get it now."
Me: "So what’s the distance between 4 and -3 on the number line?"
My wife: "7. I get it, thank you so much. Who invented this rule anyway?"
(Aside: This is not quite true. -5 – -3 is a pretty good counter-example, but I’ll talk to my wife about that tomorrow.)
I decided to go back to mathematical consistency in a different way.

Me: "Okay, let’s look at the following pattern. 4 – 3 = 1, 4 – 2 = 2, 4 – 1 = 3, 4 – 0 = 4. What do you notice?"
My wife: "Well the thing you are subtracting is getting smaller, and the answer gets bigger."
Me: "What do you think would happen if I subtracted -1? What would make this pattern consistent?"
My wife: "Well 4 – (-1) would have to be 5 then."
Me: "Right. And so then 4 – (-2) = 6, and 4 – (-3) = 7."
My wife: "Okay. I’m going to ask our son to try and explain this to me tomorrow, pretending I don’t get it. I’ll let you know if his explanation makes more sense then."
Do you have any other models I can use, should this question come up again?