Tonight my wife asked me why 4 – (-3) = 7. Apparently my son had "explained" it to her earlier tonight, but she hadn’t really understood his explanation. So I gave it a shot.
First I tried the same explanation that seemed to work for my son when he asked me what 4 – (-3) would be earlier today.
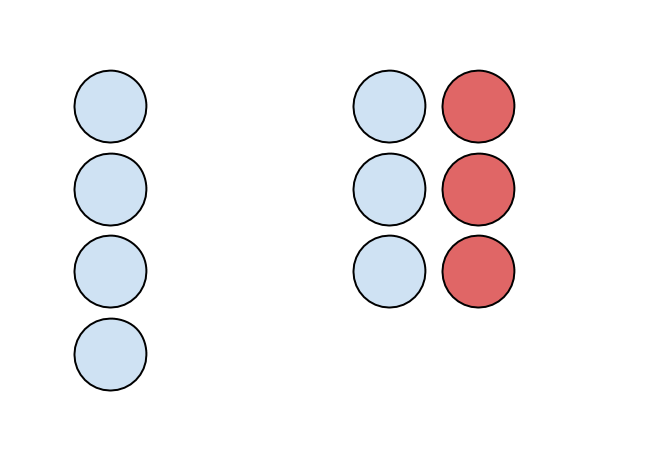
Me: "Imagine you had 4 blue circles, representing 4 positive 1s or 4 total. To this you add 1 positive circle and one negative circle. What would be the new total?"
My wife: "Still four. You added 0."
Me: "Okay, so let’s add 0 like this 3 times so the total will still be 4, right?"
My wife: "I get it. I don’t know why we are doing this, but okay."
Me: "So now, I take away the three negative circles, and therefore I am taking away a total of negative three from this picture and I’m left with 7. Therefore 4 – (-3) = 7."
My wife: "I don’t get it."
I tried a number line representation.

My wife: "I like looking at things on the number line."
Me: "Now imagine I’m on the number line at 4. If I subtracted 3, I’d end up at 1, so if I subtract -3, I must do the opposite, and so I end up at 7."
My wife: "I don’t get it."
Next, I tried operation consistency.

Me: "Okay, let’s try again. You agree that 4 + -3 = 1, right?"
My wife: "Yes. I understand that."
Me: "And 4 + 3 = 7 is obvious to you, as is 4 – 3 = 1. 4 – (-3) can’t be the same as 4 – 3, so it must be that 4 – (-3) = 7."
My wife: "That makes no sense."
I tried going back to the number line.

Me: "Okay, so what’s the distance between 5 and 2 on the number line?"
My wife: "3."
Me: "Right, since 5 – 2 is 3. Basically, one way to think of subtraction is that it gives you the distance between two points on the number line."
My wife: "Aaaaaah, I get it now."
Me: "So what’s the distance between 4 and -3 on the number line?"
My wife: "7. I get it, thank you so much. Who invented this rule anyway?"
(Aside: This is not quite true. -5 – -3 is a pretty good counter-example, but I’ll talk to my wife about that tomorrow.)
I decided to go back to mathematical consistency in a different way.

Me: "Okay, let’s look at the following pattern. 4 – 3 = 1, 4 – 2 = 2, 4 – 1 = 3, 4 – 0 = 4. What do you notice?"
My wife: "Well the thing you are subtracting is getting smaller, and the answer gets bigger."
Me: "What do you think would happen if I subtracted -1? What would make this pattern consistent?"
My wife: "Well 4 – (-1) would have to be 5 then."
Me: "Right. And so then 4 – (-2) = 6, and 4 – (-3) = 7."
My wife: "Okay. I’m going to ask our son to try and explain this to me tomorrow, pretending I don’t get it. I’ll let you know if his explanation makes more sense then."
Do you have any other models I can use, should this question come up again?
Manan Shah says:
I have always been partial to explaining this via money. Revenue is positive. Expenses are negative. Profit = revenue – expenses. Losing an expense increases profit.
October 15, 2013 — 12:28 am
Howard Phillips says:
Do be careful!!! Say I have an expense of$100. So that is -100 ?? If so then profit = income + expenses. This might be considered as nitpicking!
October 15, 2013 — 10:50 am
Manan Shah says:
You are correct to be nitpicky. I was being fast and loose with the semantics since I was on my phone. So … here’s something a bit more elaborate and hopefully more clear.
The money example is to get the student to understand that the loss / reduction of a “bad” thing (negative) is good. (In the following example let’s ignore all the craziness with accounting rules since that will truly be nitpicky 😀 .) If I have (assume a currency), revenue of $100$ and expenses of $25$, I have net profit of $75$. This is $100 – 25 = 75$. Now suppose, I decrease my expenses by $10$. This would lead to $100 – (25 – 10) = 100 – 15 = 85$. But, $100 – (25 – 10) = 100 – 25 – (-10) = 100 – 25 + 10 = 75 + 10 = 85$.
October 15, 2013 — 11:43 pm
Howard Phillips says:
This is mathematically correct…
BUT …. you are now left with the need to explain $ 100 – (25 – 10) = 100 – 25 – (-10), the bit where you have expanded the bracket !!!!!!!!
I am still looking for a real world situation in which it is necessary to subtract a negative number.
Howard
October 16, 2013 — 3:26 pm
Manan Shah says:
Sure, you have to explain the -(-10). But one can relate it to the other statement, $100 – (25 – 10) = 100 – 15 = 85$. Since $100 – 15 = 85$ so must $100 – 25 -(-10)$ and since $100 – 25 -(-10) = 75 -(-10)$ what else should $-(-10)$ be other than $+10$ if the equations are to balance?
We could go down the path of explaining $-(-10)$ as $(-1)*(-10) = (-1)*((-1)*10) = (-1)*(-1)*10$ but then I think “explaining subtracting negative numbers to my wife” may lead to “my wife divorced me because I tried explaining subtracting negative numbers”. But perhaps the explanation I gave may lead to the same consequence, for better or worse.
October 17, 2013 — 10:48 am
David Wees says:
Fortunately for me, my wife is not likely to divorce me because of a poor explanation of something. She has plenty of prior experience in this area. Apparently she thinks my verbal communication skills need work.
October 17, 2013 — 11:57 am
Dan Pearcy says:
One conceptual way: Draw a timeline from 500BC to 2000AD.
What’s the difference between 2000AD and 1600AD. Same thing as 2000 – 1600 = 400 years.
Now, what’s the difference between 2000AD and 100BC. Same thing as 2000 – -100 = 2100 years.
That’s helped my wife! 🙂
October 15, 2013 — 1:56 am
Jason Mestinsek says:
I made a clip on my YouTube channel ‘MrMeznik’ to explain this to my students that I call ‘happy/sad number line ‘
Also try James Tantons explanations using ‘holes’ and ‘piles ‘ on jamestanton.com.
Cheers!
Jason
October 15, 2013 — 2:38 am
Jim Doherty says:
David
What I think I like the most about this is that it hints at how often students will say that they ‘get it’ when they do not. Bravo to your wife for being persistent in saying that she was not comfortable with this until she finally was. Bravo to you for being patient and trying again and again. I have to imagine that almost any student will give in after two or three explanations, stop trying to really understand and simply parrot the pattern in front of them.
October 15, 2013 — 7:08 am
Howard Phillips says:
The trouble with numbers is that they arise from two different real world situations: Counting and Measuring. Negative numbers arise from a particular type of measurement, relative position. We do not have -3 apples, we do not have -10lb of sugar, we have created negative numbers to deal with temperature, height above sea level, voltage and other such things that are measured relative to an (often arbitrary) zero. Consequently the original notion of subtraction which is ‘take away’ is meaningless in this new situation. Finding a real (not artificial) example of subtraction of negative numbers is almost impossible. In mathematics the situation 5-(-7) only turns up once you are in algebra, and the ‘explanation’ can come from a sensible interpretation of straight line graphs etc. Best to leave the thing alone until it forces its attention on one.
October 15, 2013 — 9:54 am
Howard Phillips says:
Alternatively, 4-3 is a meaningful subtraction but 3-5 is not. What it really means is 3+(-5). So 3-(-5) means 3+(-(-5)), which leaves the need to find a meaning for -(-5). This leads to multiplication, in particular the reasonable assertion that -5 is (-1)*5, and the multiplication sign is highly desirable here. So -(-5) is now (-1)*((-1)*5), or with fewer brackets, (-1)*(-1)*5. Consequently the whole business is based on the meaning ascribed to (-1)*(-1)……….
October 15, 2013 — 10:37 am
David Radcliffe says:
I’ve had limited success with the number line model. For me, it comes down to the fact that subtraction is the inverse operation for addition. What must be added to -3 to get a sum of 4?
I tell students that there are two ways to interpret subtraction: “take away” and “how many more?” We can subtract 10 – 7 to answer the question “How much is left when 7 is taken away from 10?”, but it also answers the question “How much bigger is 10 than 7?”. The second interpretation is often more useful for subtraction of integers.
October 15, 2013 — 1:50 pm
Krystine says:
I’ve seen it explained as positive being true and negative big false… It took me a minute, but the kid said “If positive is true and negative is false, then a plus plus means it’s true that it’s true, and minus minus means it’s false that it’s false, so those are both true (or positives). If you have a plus minus it’s true that it’s false and for minus plus it’s false that it’s true, so those are both false ( or negative). True means it’s right so it goes right on the number line and false means it goes left.” It was quite convoluted, but the kid had a point 🙂
October 16, 2013 — 1:57 am
Bryan Meyer says:
Not sure if you quoted the conversation exchange verbatim (or at least as close as you remembered it), but I couldn’t help noticing that in the last example you ASKED “what do YOU notice” and “what do YOU THINK the next one would be” instead of trying to explain it. I wonder if that had any impact on her making connections?
October 30, 2013 — 2:54 pm
David Wees says:
It’s a good question Brian. I’m not sure if this is exactly what was said. I wrote down a few hours later. I know that these are the examples I used because I had the scrap paper to look at when recording them.
October 30, 2013 — 9:48 pm
Ronald Fischman says:
I always used money. I have seven dollars in my wallet, but I have to pay you three when I see you later in the day. This means that I only have four dollars f’real, unless I’m willing to face down your friends in a back alley. My uncle runs into you, and pays off my three dollar debt.
He took away (that’s a subtraction) my debt (that’s a negative number). So now I get to keep all seven of my dollars. So, $4 minus (-$3) is $7.
Q.E.D. (I hope)
August 26, 2014 — 4:22 pm
@mr.leiss says:
Hi David,
The distance model still works as long as you begin at the second number and move to the first. The direction of travel can be used to interpret positive or negative numbers.
4-2=2, moves two to the right; while -4–2=-2, as -2 would move two to the left.
I don’t have a lot if experience teaching this to students yet, but I try to keep consistent to this as the model of number line subtraction and use counters or other physical objects for the adding / removing models.
I also like the counter model, but I think it helps to start with the question and then try to build a specific model of, say, subtracting 2 red (-) from a pile of 3 yellow (+) counters. We can’t take away what we don’t have, but we can add some reds to our pile as long as we balance with yellows, then we can subtract and see what’s left.
August 28, 2014 — 8:24 pm
Harold Rene' Mancini says:
I usually go with what I now see is a complicated way: I say that 1 is a shy number that doesn’t like to show itself, but still we can make it appear. This way i re write 4 -(-3) as 4 -1(-3), then I recall that the moltiplication sign is lazy so some times it appears sometimes not, thus I can make another change 4 -1*(-3). At this point I have to recall that minus time minus equal plus, so we have 4 + 3 = 7. [My analysis I teacher said that I have a very complicated brain ^^ ]
May 5, 2021 — 2:15 pm
Santika Scruggs says:
2+16 =18
May 6, 2023 — 9:03 pm