Here are at least six problems that often make inquiry-based lessons fail.
Some Problems
- Students have too much information to process when attempting to solve a problem which can quickly overwhelm their working memory.
- When given a new problem type, students do not always have all of the prerequisite knowledge necessary to approach the new problem successfully, leading them to need to make leaps of logic larger than they are able.
- When students are sharing their ideas and strategies for solving a problem, other students are either not really listening or hearing what they want to hear rather than what is actually being said.
- Students sometimes focus on the short-term “How do we solve this type of problem?” rather than “What mathematical principle can I generalize to be able to solve other problems?”
Alternatively, students attempt to generalize and run out of working memory since they often have to hold both their solution and the generalizations from their solution simultaneously in their heads in order to generalize. - The goals and/or structure of inquiry-based lessons are often unclear. When students need to remember the goal of a lesson and the structure of an activity in order to be successful, they have less working memory available to actually be able to focus on the task at hand – the problem they are working on.
- Students often use “means-end analysis” when problem solving which means they tend to focus less on what process they are using (and improving that process) and more on what answer will get them out of needing to continue problem solving.
Some solutions
Note: The solutions described below assume that your lesson structure is still inquiry-based. It may be that the best solution to whatever goal you have for the day is not to use inquiry at all, but have students study worked examples instead.
There are a variety of solutions to problems 1, 2, 4, and 6 which are all based on problem-structure and task selection.
For example, in the instructional routine Connecting Representations, the goal of any given task is not to come up with answers to problems but to name connections between two representation types. Students are focused on a small amount of information at any given time, which is given students in a deliberately staggered way in order to reduce the amount of information to process all at once. Connections between representation types are also easier to generalize than solutions to problems.
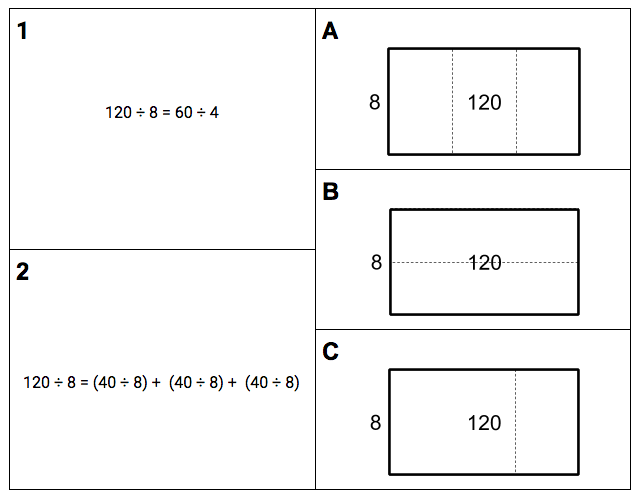
A sample Connecting Representation task
To improve the odds that students can generalize from their problem-solving experience, make generalizations a focus of any whole group discussion following the problem-solving time and have students reflect (in writing, perhaps in a regular journal) on what they learned today that they think they may be able to use in the future. Sentence prompts like “Today I learned to pay attention to … because …” can scaffold these reflections for students.
Another suggestion is to select tasks for which students can use a lot of what they already know to solve the problem and only have to make small leaps. We want to balance our students’ use of their long-term memory to aid them in solving problems with their working memory to make the small new leaps or connections necessary. A good rule of thumb is that if students need to make 3 or more small discoveries or new connections in the course of solving any particular problem, they probably won’t.
We’ve also noticed in our work that it can be helpful to distribute problem solving tasks both over time and over a group of people.
Distributing a problem solving task over time means giving out portions of the problem to learners in smaller chunks rather than all at once. For example, it can be really helpful to give students some independent time to first consider a problem on their own before working with a partner. Or you can divide a more complex problem solving task into smaller pieces so that students can “chunk” their earlier work into their later, more complex solutions. The Math Forum’s “Notice and Wonder” protocol is one example of this principle being used in practice.
Distributing a problem solving task over a group of people means giving learners deliberate access to each other as resources while they are problem solving.
In Peter Liljedahl‘s “Building Thinking Classrooms” work, this looks like students working at vertical whiteboards in small groups or with a partner, during which I have often noticed groups borrowing ideas from each other.
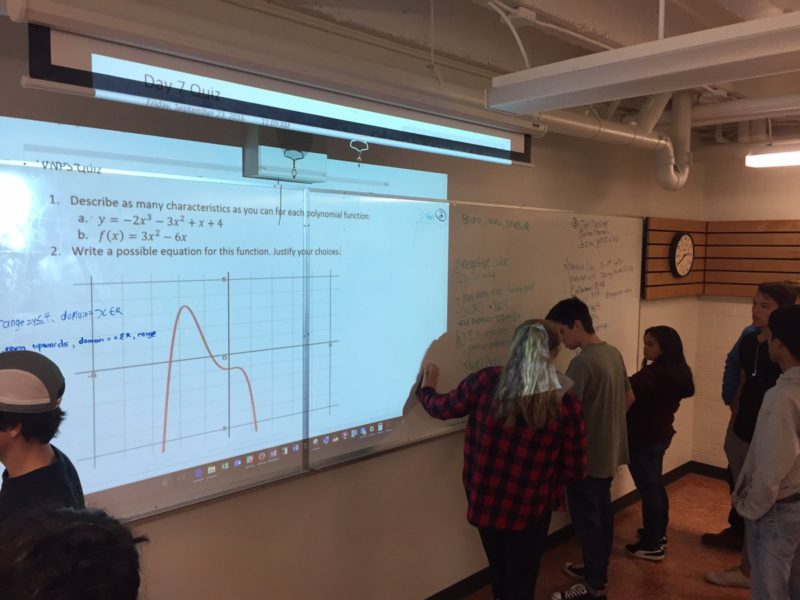
An example of the use of vertical nonpermanent surfaces, shared with permission from Michael Pruner.
In our work with instructional routines (with lots of help from Grace Kelemanik and Amy Lucenta) this means making problem solving sessions short and/or interrupting an unsuccessful problem solving session with whole class opportunities for students to share observations and ideas. In order to improve the odds that students actually listen to and understand each other (and solve problem #3 listed above), we have students first share a strategy/idea while we or a student points, then another student restates a strategy/idea while we either continue to point, another student points, or we annotate the strategy using color/symbols/small amounts of text. We have also found it helpful to press students to provide complete explanations, especially when there are missing details/jumps in logic in their explanations.
To get a sense of how this supports students, try watching the following two videos to see how the use of restating and annotation makes a huge difference in your own clarity around a strategy being shared.
Student sharing a strategy: no gesturing or annotation
Student sharing a strategy: with gesturing and annotation
In terms of the 5th problem with inquiry, around the goals and structures of a lesson being unclear, I’ve written extensively here about how instructional routines support students (and their teachers) in minimizing unnecessary extraneous cognitive load focused on “what am i doing next?” If you don’t have time to read that other post, tl;dr: routines free up working memory by allowing students to delegate questions about what their role is, what they are doing next, and why they are doing it, to their long-term memory.
Conclusion:
In many schools around the world, learning how to use inquiry-focused lessons in mathematics class is a focus of the school or mathematics department. However, inquiry-focused lessons come with their own set of challenges, raised above.
I have some proposed solutions to those challenges listed above, but I’d love to hear what other people are doing to tackle the same problems or what other problems people have noticed occur when they try to implement inquiry-focused lessons.
Ben says:
Here’s my recent riff on the same subject: http://mymathclub.blogspot.com/2017/02/making-explorations-successful.html
I use inquiry all the time but what I notice is hard is that pacing is difficult. Everyone does not end in the same place without a group discussion at the end to distribute knowledge. I’m not entirely happy with that structure since I do want everyone to make breakthroughs.
I’ll also note that Peter Liljedahl always pairs white-boarding with visible random groupings.
May 26, 2017 — 7:16 pm
Eric Nelson says:
Cognitive science emphasizes that conceptual understanding is vitally important in mathematics and it needs to be taught (Siegler and Lortie-Forgues 2015).
In the National Mathematics Advisory Panel Report, Chapter 4, Geary et al. (2008) write:
“[T]he cognitive processes that facilitate rote retention (e.g., of over-learned arithmetic facts), such as repeated practice, can differ from the processes that facilitate transfer and long-term retention, such as conceptual understanding.”
At the right time, Clark et al. (2012) note that less-structured problem-solving activities can be useful:
“Independent problems and projects can be effective – not as vehicles for making discoveries, but as a means of practicing recently learned content and skills.”
The key is: Facts must be well memorized BEFORE conceptual frameworks can be constructed by inquiry or other means.
For how this applies to the US Common Core math standards, see http://www.ChemReview.Net/ccms.pdf
May 26, 2017 — 11:10 pm
Jen says:
You mention that some students don’t listen but the other HUGE component is that the social interaction itself takes up working memory. Any issues that may exist between certain student that the teacher is unaware of can completely undermine any learning that is supposed to take place.
May 27, 2017 — 1:53 am
David Wees says:
Those are both true, but there is significant research into the benefits of cooperative learning, which often has no supports given to it at all. We’ve found that the use of instructional routines which embed students understanding their role, having sentence prompts to use to discuss ideas, etc… all of which helps improve the quality of the peer to peer interactions that occur in small groups (or ideally partners since this raises individual accountability), and there are parallel supports for when students are sharing their work in a whole group setting.
May 27, 2017 — 4:02 am
Peter Smyth says:
These are great ideas.
I think the greatest challenge is to find the teachers who have or are willing to change their relationship to their own mathematics. Deb Ball talked about MKT, the Mathematical Knowledge for teaching.
Fot me, inquiry – thinking – has to underlying all mathematics teaching; otherwise we’re teaching something else.
So the deep question is how do give teachers to opportunities to transform themselves?
May 27, 2017 — 3:54 pm
David Wees says:
In our project, we teach teachers the inquiry-focused instructional routines we use by first modeling them as teachers with the teachers in the workshop playing the role of students. This helps give teachers some experience learning math in a way often very different than how they were taught. Early in our work Grace Kelemanik suggested modeling an instructional routine three times with teachers so that they get a sense of what is fixed within the routine and what depends on the mathematical task and teacher goals.
I always try to include at least one example task with any particular routine where it seems likely to me that a majority of teachers will learn some new math, even if the task itself may not be especially helpful with their own students, so that they get the experience of what it feels like to learn math in our inquiry-focused environment.
May 29, 2017 — 9:46 pm
John Golden says:
David, what a helpful post. So often the discussion stops at inquiry or not, rather than inquiry, now what? It also makes some non-blaming space for teachers who have tried inquiry and not found it to be helpful.
The main problem I’d add is student expectations. They have been conditioned to expect I’ll show you how, then you’ll repeat. That makes these lessons frustrating for them (“I just don’t learn that way”) as well as misleading them as to what learning and understanding is.
May 27, 2017 — 6:39 pm
David Wees says:
I think student expectations can be managed by starting with tasks that they can do on their own, so that they experience success, and then learn how their role works within the inquiry-routine you use.
May 29, 2017 — 9:41 pm
Henri Picciotto says:
Great topic. In my own teaching, inquiry is guided, by which I mean (more or less):
– start with an overarching question that students understand (not that they know how to answer it — but they know what is being asked)
– provide some guidance in the worksheet (see examples on my Web site — MathEducationPage.org)
– provide hints as needed as groups are working
– interrupt group work whenever more than one group is stuck, for whole-class sharing and discussion
Unguided inquiry only becomes possible after students have developed the needed habits of mind with much practice in guided inquiry.
May 27, 2017 — 11:49 pm
David Wees says:
Hi Henri,
Do you have any structures in place to help groups work together and actually listen to each other? So often I sit down and listen to kids working in a group and many times they all but ignore what each other is saying and doing. I think this may be related to the demands of the task but if they know really well how to best work with each other, then when the work gets tougher, I feel like it will be easier for students to work productively together.
David
May 29, 2017 — 9:40 pm
Michael Pershan says:
Great post! Lots of good advice.
One thing I’ll add is that I like to tack on a bit of related practice to the end of my ‘inquiry’ tasks. This is aimed at assessment but also at the generalizing that you mention.
I don’t think that’s special advice about inquiry-based lessons, though. Ending a whole-group ANYTHING with some practice seems like it might often be a good generalizing move.
May 28, 2017 — 7:41 pm
David Wees says:
I agree, Michael. You can also embed some practice into the inquiry lesson itself. Here’s an example of that.
May 28, 2017 — 8:06 pm
Dan Meyer says:
What is the definition of “inquiry” you’re operating with in this post?
May 29, 2017 — 6:13 pm
David Wees says:
That’s a really great question. I’d say, any time students are presented with problems that they haven’t been shown how to solve the problems is a form of inquiry.
This definition of ambitious teaching might be helpful:
Another useful essay that describes the kind of inquiry I imagined when writing this post is Cathy Seeley’s “Essay #12: The Upside-Down Classroom” or as Magdalene Lampert slightly modifies it, “You do, Y’all do, We do”.
May 29, 2017 — 9:22 pm
Michael Pershan says:
Honestly, I think this is a pretty good definition. But since I think it’s helpful to push on definitions and see whether they break, here’s a thought I had about this definition.
Say that I present students with a completely worked-out example for how to solve a linear equation. I present it to students. I say, here’s what I’d like you to do. I’d like you to study this, ask me questions, and try out using this same method for this related question over here.
I claim that this is inquiry-learning, seeing as I’ve never told students how to solve a linear equation before. They’ll have to discover how to understand this worked-out example all on their own.
Like I said, I know I’m being annoying here. But I was trying to think of an example that would capture my feeling that all understanding involves a moment of discovery and the attempt to understand deserves to be called inquiry. Have I succeeded?
May 29, 2017 — 9:48 pm
Michael Pershan says:
…aaaaaand, I just discovered that the ‘blockquote’ tag doesn’t work on your comments. Sorry!
May 29, 2017 — 9:49 pm
David Wees says:
I just noticed the blockquote issue, thanks for bringing it to my attention. I added some css to make blockquotes stand out better.
Now I’m thinking about your example. I guess the worked example in the way you suggested using it is a form of inquiry, in the sense that the student has to decide what elements of the worked example to pay attention to. Certainly we used worked examples all over the place in our curriculum work.
I wonder though if you told students what to pay attention to, and then checked several times to make sure that they paid attention to it in the way that you suggested, and then gave students feedback on their ability to pay attention to the features you think are important, this would be less-inquiry focused on some sliding scale between “no inquiry at all” (which maybe is never completely possible) and “here’s some blank paper, invent all of math on your own.”
May 29, 2017 — 10:00 pm
Henri Picciotto says:
Helping groups work better: my strategy, far better in my view than assigned roles or general teacher speeches, is direct intervention.
If a student is not being listened to, say “wait! Lucy said something important. Listen to her. Lucy: say it again” If a student doesn’t listen to anybody and sits away from the table: “Joey, pull your chair in and lean in. You can’t participate sitting like this.” And so on. It is not a good idea to just watch groups as they flounder,
But also: not all tasks require groups to work as groups. In my class, group work often means working individually, with the option to ask for help from neighbors or teacher, and the responsibility to offer help when asked. That too works as training for activities that require participation of all four kids.
May 30, 2017 — 2:00 pm
Piers says:
Great post – thank you.
Point 3 is a tricky one, I find, not least because of the pros and cons of different make-ups of groups (friends, abilities etc).
The 2 strategies I’ve found most effective are Think-Pair-Share (http://www.readwritethink.org/professional-development/strategy-guides/using-think-pair-share-30626.html) and the Envoys one described here:
May 30, 2017 — 7:21 pm