Here is a question I was asked recently.
A student asks you why 0 to the 1st power is 1. What do you do to help the student understand?
Any time a student comes to me with a question, I try and see if I can figure out what’s going on by paying careful attention to the student’s explanation of the thinking that led to come to their current conclusion. In other words, I make an attempt to assess what they understand and use this to diagnose what’s going on.
Depending on what issues I discover the student has, I might address this by addressing their pre-requisite misconceptions, create an activity for them to do, ask them questions to help them draw out a better understanding of the problem, or by involving a peer to have them help explain the concept.
In this specific case, if the student asks this question, chances are they are misremembering the "rule" that says that x0 = 1 for all x except x = 0 (at x = 0, the expression is undefined, which could possibly lead to a really interesting investigation for students). A student who misremembers this rule has probably learned it by memorizing it, and may lack understanding of where this rule comes from. It may also be that they do not really understand what exponents are. It may also be that the student does not yet understand division and multiplication thoroughly, as these are pre-requisites to really understanding exponents.
A simple investigation that may address this is as follows.
First we look at this pattern:
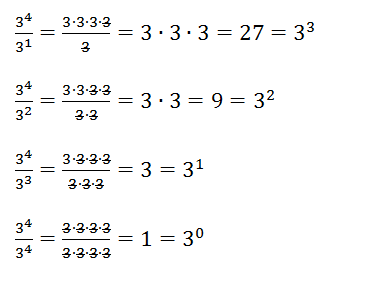
Next we ask the student, what do you notice about this pattern? What would happen if we changed all the threes to 7s or 2s? Would the result still be true? How could we generalize this pattern we have discovered? At this stage, the student might recognize their misconception and be able to move on. If the student is not proficient with exponents at this stage, they may need a more broad investigation into the other exponent rules.
According to this summary of research on student understanding of exponents, they often feel that exponents lack connection to the real world (Senay, 2002), and do not understand the point of studying them. A student who struggles to to understand a concept involving exponents may be resistant to the concept simply because they cannot see the value in it. One way to address this is to choose specific examples where exponents make the problem or idea in the real world much more easy to understand. The Powers of Ten website may address this to some degree, as may the story of the farmer and the king. There are also many other resources available which may help students see the value in learning more about exponents.
Another option, if the student has a good understanding of graphs, is to try and have the student produce the graph of a function like y = 2x for x > 0. They can do this with a table of values using x = 1, x = 2, x = 3, x = 4, x = 5, etc…, and then attempt to fit a nice exponential curve to the existing points. Extrapolating the curve back to x = 0 should lead the student to see that the result is not likely to be 0, and if they are lucky, they may get close to the actual value of 1. This may make another approach, like the experimental one given above, seem more realistic.
Another option is to look at decreasing values of exponents.
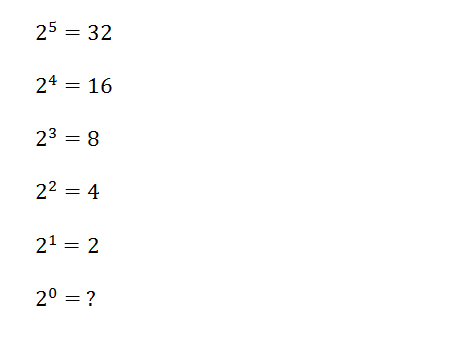
Again, the purpose here is to get the student to look at the pattern and try and draw some conclusions. What value of the question mark would make this pattern work nicely? This will help students see that the rules we are using are intended to create consistency within our use of exponents, and preserve some of these patterns.
While I am working with the student, I try to use good questions. If the student asks questions, I try to respond in such a way so as to make them continue thinking. My objective is to provide students with tools they can use to figure out the solution to mathematical problems themselves so that we can work them toward being independent from their teachers.
Can you recommend some other ways I could help this hypothetical student understand exponents better?
Shawn Urban says:
I learned the pattern using the rule that exponential numbers, sans base 0, always had 1 as a factor. So 2^3 = 8 = 1 x 2 x 2 x 2, 2^2 = 4 = 1 x 2 x 2, 2^1 = 2 = 1 x 2, 2^0 = 1 = 1. Exploring base 0 is always a challenge, but also informative. I like going back to patterns to explain algorithms.
By the way, I like the new blog look.
December 20, 2012 — 2:45 am
Sue Jones says:
I’ve been wondering whether to include the zero power earlier in instruction, for starters, tho’ I’m disinclined because, in general, we throw too much at people at the same time, especially since saying 3^1 was 1 x three would reinforce the misconception that the power number shows up in the process.
I usually talk about the temptation to say the answer is zero, and if I’m in proper “get the student to talk” mode I’ll see if I can get the student to acknowledge that multiplying by zero gets an answer of zero… and then I’ll remind them of that odd thing about exponents: that 5 to the second power isn’t being multiplied by two, is it? There’s no two in there at all… that you’re not multiplying by zero, either.
Then I’ll do one of those logical progressions you outlined… trying to emphasize the math that is happening — that to drop down a power, you divide by that number.
Then, for my folks who like a drama with everything, I’ll note that zero has a *ton* of power in multiplying — it turns things into zero! The number in multiplication that has no power and doesn’t change anything is one. When we raise a number to the zero power, we are zapping away the power of that number and reducing that poor thing to one.
December 20, 2012 — 10:41 am
Scipi says:
I show this same pattern to demonstrate what happens when the exponent is negative.
January 16, 2013 — 10:29 am
David Wees says:
I do this as well, and I also use the "rule" (subtract the exponents when dividing numbers with equal bases) as a justification for negative exponents. However, an investigation approach is very useful here as I feel students will have a way to refigure out a rule if they forget it later.
January 16, 2013 — 11:40 am