Here is a transcript from part of a classroom discussion.

Student: “So, I think.. well we believe, we noticed that expression number two combines with vision number B because it’s parenthesis x plus two, right?So all the visions and all the squares are repeated three times because it’s being multiplied by three. And so the x I believe, well we believe, would be the rectangle and the squares would be the two.”

What do you think is being discussed in this example? It’s impossible to understand this conversation without a visual representation. So, let’s look at the task the students are talking about.

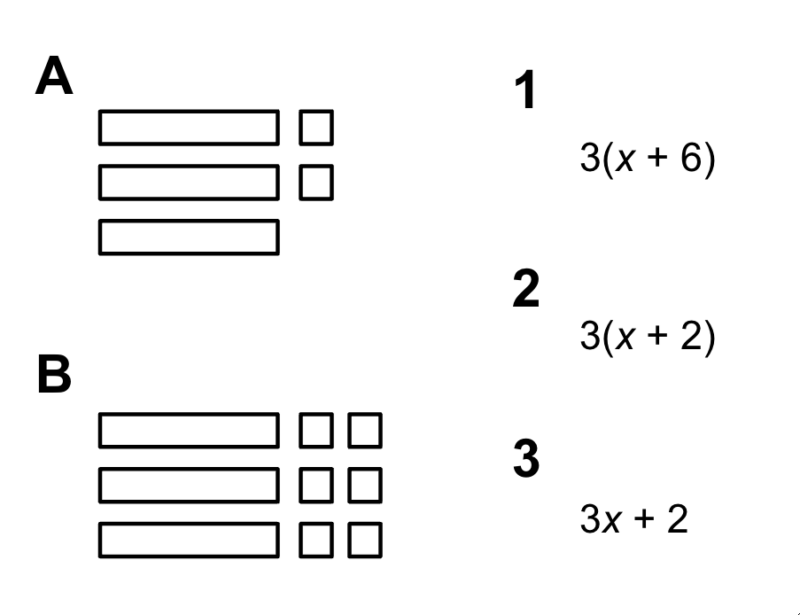
2 visual representations are present. The first visual, A, shows 3 rectangles and 2 squares. The second visual, B, shows 3 rectangles and six squares, with 1 rectangle being paired with 2 squares, three times. There are also 3 expressions, numbered 1, 2, and 3, which are 3(x+6), 3(x+2), and 3x+2, respectively.

Now, consider the same questions. What mathematics is being discussed?

Let’s look at the task again but with some annotation meant to draw students’ attention to the salient details of the explanation.

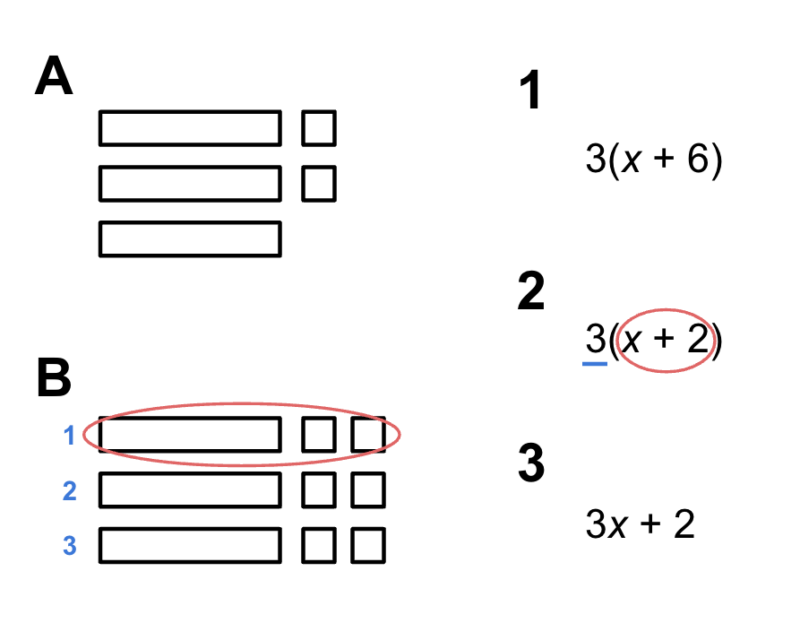
2 visual representations are present. The first visual, A, shows 3 rectangles and 2 squares. The second visual, B, shows 3 rectangles and six squares, with 1 rectangle being paired with 2 squares, three times. There are also 3 expressions, numbered 1, 2, and 3, which are 3(x+6), 3(x+2), and 3x+2, respectively. A red oval is drawn around both the x+2 in the 2nd expression and one rectangle and a pair of squares in visual B. A blue underline is under the 3 in the expression 3(x+2) and the 3 rectangle plus 2 squares are numbered 1, 2, and 3.

Now imagine the conversation. What is being discussed? What strategy is being shared?

Here is a generalizable principle: if one doesn’t have a visual way for students to track a conversation, one should assume they cannot.

Facebooktwitterredditpinterestlinkedinmail