Tag: The Reflective Educator (page 2 of 43)

From Facebook:

“my daughter and I were brought in to talk about her ” learning disabilities ” and how she was not applying herself . They talked about punishments and incentives . After listening to everyone I asked . ” If I asked you to build a nuclear power plant could you do it ?” They all answered ” no ” So I ask well what if i took a way all your free time at work , and did not allow you to go to the ofice party because you could not build it ? Could you build it then ?” Again the answer came back No . So I ask ” Okay then how about if I promise you a huge reward , could you build it then ?” Again they all answered no . So I say ” what if I read you a manual on how to build a nuclear power plant , gave you people who were educated and worked building nuclear power plants to show you how to build one , gave you every tool , all the materials to build one , could you build one now ” one said no still , but the rest said maybe . well I said to them my kid cant do this work if you punish her for not doing it ,or promise her a pizza party. She will only do this work if you put her with people who can help her understand . The world is a power plant to her .” [sic] ~ Adriene Kimiko Pauley

Could you build a nuclear power plant given the right reward? Or would you need support just to be able to get started?

I was not born a technology person. 

I am a person who does not accept that he does not know how to do something related to technology and explores how he does it until he figures it out. I am a person who will occasionally search to the fifteenth page of a Google search until I find the right piece of knowledge that helps me figure out my problem. I am a person who believes that I can eventually figure out any technological problem I am given, even if the answer sometimes is to find someone with more expertise. I am a person a who has been exploring the use of technology since I was inspired by the gift of my first personal computer at eight years old.

I was not born a mathematician.

I am a person who has been exploring numbers since before he started school, supported by a home environment rich in numbers and geometry. I am a person whose parents never told me that math was hard. I am a person who found solace in exploring ideas when he found out that kids can be cruel. I am a person who had a pair of exceptional mathematics teachers from grade four to grade six who taught me that mathematical ideas weren’t just meant to be written down and forgotten later but discussed and explored. I am a person who has studied mathematics for nearly 35 years.

I was not born to teach.

I am a person who often dreaded going to school as a young child either because I was bored or bullied. I am a person who struggled to make friends at school and never really understood other people. I am a person who decided to take musical theatre just to be part of the cool crowd in middle school. I am a person who needed to fill a block in eleventh grade and got pushed into peer tutoring by his guidance counsellor. I am a person who learned that he loved it when he could help other people understand. I am a person who worked hard every moment he was in his teaching program to the point of being called driven by his friends. I am a person who nearly gave up teaching in his first year because of how hard it was. I am a person who only survived his first year of teaching because he found out other people in his school were struggling as much as he was. I am a person who has dedicated a large portion of his life to learning more and more about the relationship between teaching and learning for the last twelve years of my life.

When we see someone who seems to do something well, we have the tendency to assume that they have special talent, rather than they had a set of experiences that prepared them to be successful.

Much of the research on formative assessment suggests that grades are not effective as feedback because they do not provide students with actionable information they can use to move their learning forward. Comments and questions are much more useful to students when grades are not included.

Unfortunately, if you have 180 students, providing individualized feedback to each student regularly is time-consuming and difficult, maybe even impossible. Grades are much easier to produce. 

One partial solution to this is to produce a list of descriptive comments and select the comments you want for each student from this list. Since students often require the same feedback, this provides enough individualization that is still helpful for the student without being over-whelming for teachers to actually do. One way to do this is to create a 1 or 2 page list of the comments and then check-off the comments that actually apply to the individual student, and then give each student their individually selected comments. Unfortunately, while not as time-consuming for teachers, this leaves students having to read a bunch of comments or questions that do not actually apply to them. (Aside: One interesting activity here would be to provide students with the complete list of possible comments and ask them to figure out which comments probably apply to their work.)

It is possible to do both; provide students with an uncluttered list of comments that apply to their work and not have it take an enormous amount of time. The best part of the process I’ve come up is that you get to keep a copy of the comments you actually gave to students for further reference.

This process uses Google Spreadsheets and the Autocrat add-on from New Visions to turn a template for comments into individual comment documents for each student. If you are using a non-Google Apps for Education account for this process, you should probably not include identifying student information in your personal Google account and just print these documents to share with students.

The first step is to create a Google Spreadsheet and enable the Autocrat add-on. For more information on the Autocrat add-on, see this page. I also recommend creating a folder for each assignment to keep all of the comment documents in. You may also find that this process plays well with Doctupus if you are already using it.

The next step is to enter in names and email addresses for each of your students as in this sample spreadsheet. If you want to avoid storing student information in a Google Spreadsheet, you could use pseudonyms at this stage and enter your own email address, and then print the comments once they are created. Otherwise, you can choose either to print the comments or share them with students electronically.

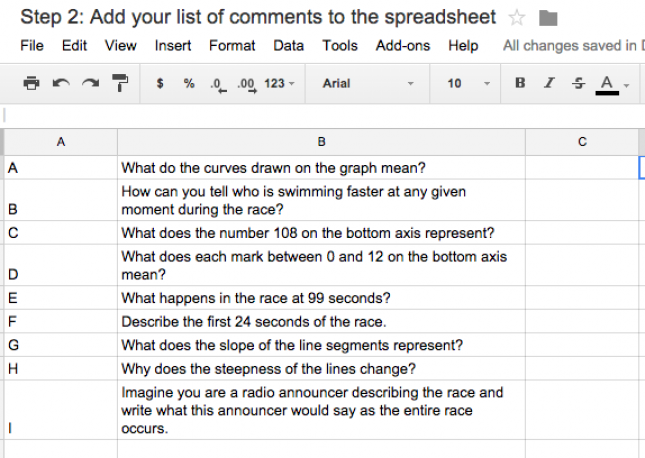
Now, in this spreadsheet create another tab. Into this new sheet, enter letters from A to Z as necessary into column 1, and enter comments, questions, or other feedback into column 2. These comments should be relatively generic but apply to specific common issues you have noticed in the student work. Remember that every one of your students, even the ones who did very well on the assignment, need constructive feedback to move their learning forward. The comments shown below are associated with with this mathematics task.

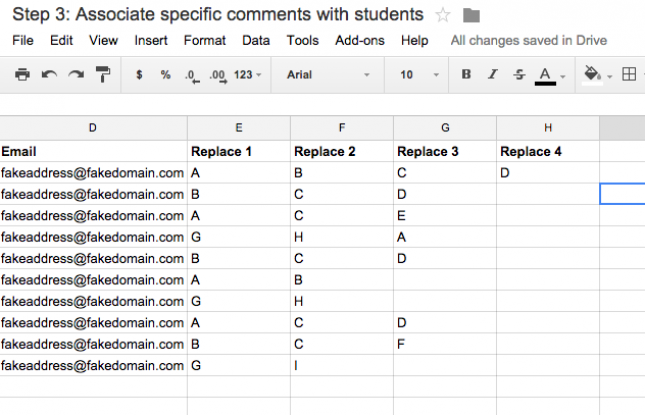
Now it is time to associate these comments with specific students. Create a number of columns equal to the maximum number of comments you think you will give to any individual student. The title of these columns doesn’t matter, but I used Replace 1, Replace 2, Replace 3, etc… to help remind me that these comments are not the ones I intend to share with students. Instead, in these columns place the letters associated with the comments you want to give students instead. You may find it helpful to print the sheet of comments and their associated letters from step 2 to help enter comments when you look at student work. Notice that I have left some of the cells below blank since I only have 2 or 3 comments for those students.

The next step makes those letters useful for students. Instead of sharing the letters with students, you want to share the comments. Here is where I used a Google formula to take the letters and substitute them for comments in another cell. The actual formula itself will depend on the name you used for the comment sheet you created in step 2 and the number of comments intend to share with each student.

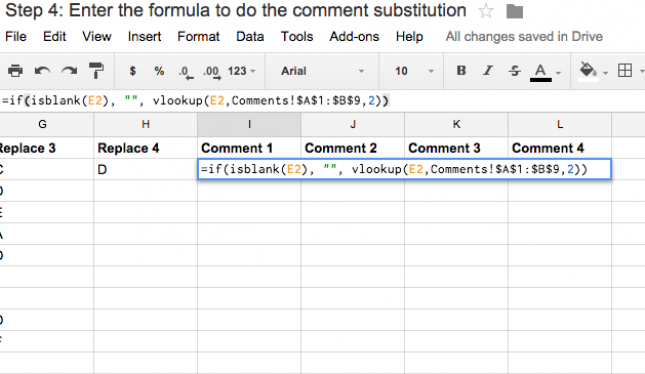
The formula I used is =if(isblank(E2), “”, vlookup(E2,Comments!$A:$B,2)) which you can copy and paste into the top-left most cell of your comment columns as shown above, and then edit to meet your needs. Basically what this formula does is check to see if the associated cell (E2 in this case) is empty, and if it is not empty, it looks up the comment in the sheet you created in step 2 that is next to the letter entered. If you need to edit this formula, E2 refers to the top-left most cell where you entered the letters corresponding to the comments, and Comments! refers to the name of sheet with the comments in it that you entered in step 2, and finally $A:$B refers to the two columns from the Comments sheet where you entered the letters and comments. Once you have the formula entered into this cell, you can drag it over and down to fill all of the relevant comments, as shown in the brief video below.

You will also need a template document like this one. Autocrat will take this template document you create, make a copy of it as either a PDF or Google Doc for each student, and replace the variables entered into the template (which look like <<Comment 1>> in this sample) with the comment information you entered into the spreadsheet.

Now you have all of the preparation work done that you need to run Autocrat. Launch Autocrat from the menu above (if you have not added Autocrat to the spreadsheet, you will have to do this now).

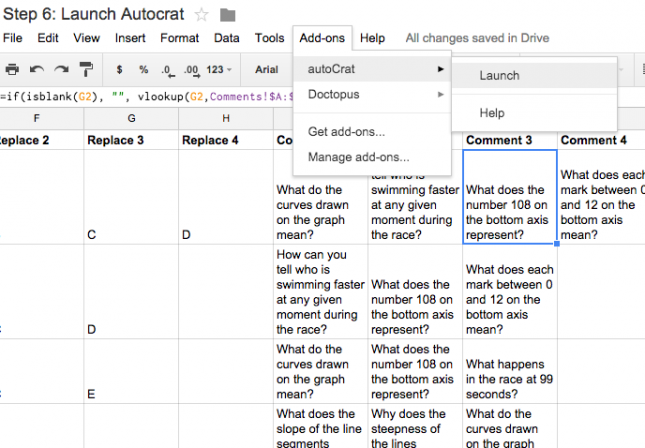
Click on New Merge Job in the new Autocrat sidebar.

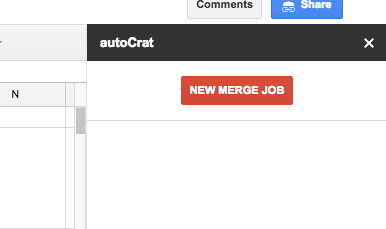
Click on Drive in order to select the Google Doc template you created and then give the merge job a name.

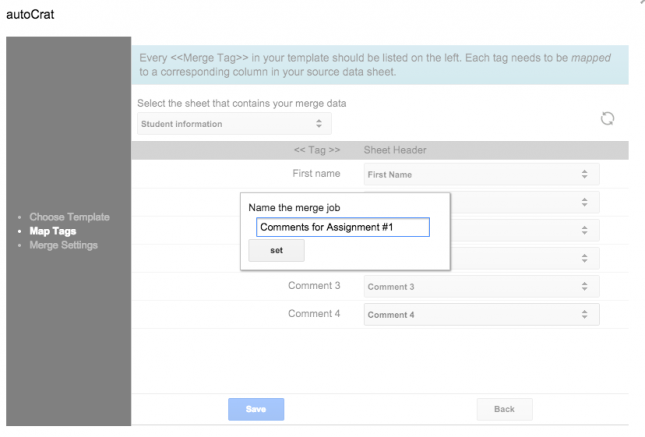
Confirm that the <<tag>> and Sheet header information is correctly set. Here Autocrat has attempted to match the headers of this spreadsheet with the variables you entered into the Google Doc template.

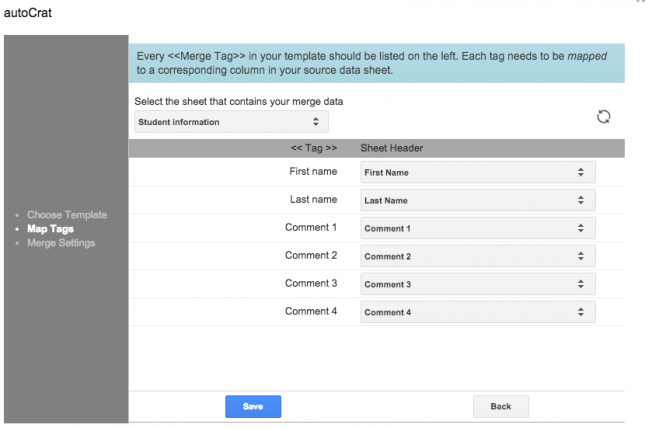
Click Save, and then enter the naming format each document to be shared with students should have. You may also want to open up the advanced settings here and select a folder for these documents to be created in.

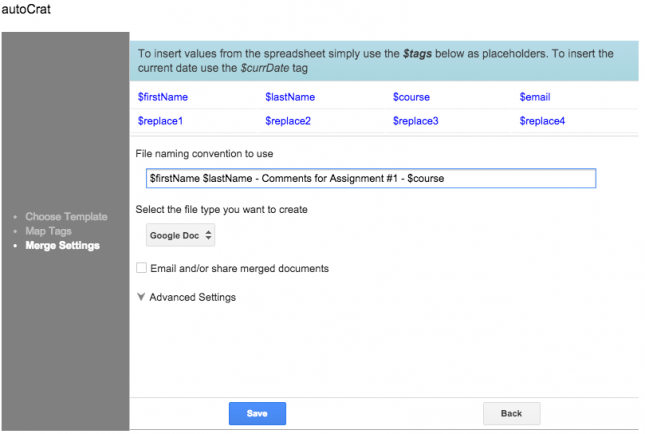
Now you should be able to click on the Run Merge button on the right. Autocrat will share a copy of the template with each email address entered into the email column with the comments entered instead of the variables. You may want to click on Preview before running the merge, just to see what the documents will actually look like before they are created. Once the merge is done, the documents will exist, be shared with students (assuming you entered their email addresses and not your own), and there will be links to the documents in this spreadsheet.

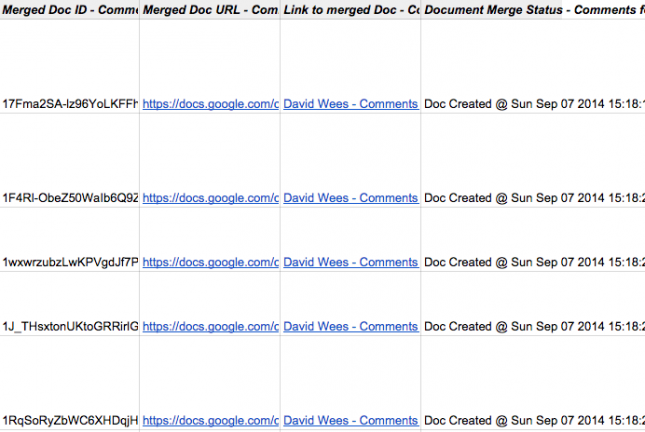
Here’s what a folder of these comment documents looks like. At this point you can download these documents (you can download all of the files in this folder as a zip archive, and then once you extract them from the zip, print them out for students – you can do batch printing in both Windows and Mac OS) and then print them out for students or students can access the documents themselves online.

The good news is that once you have set up this process once, replicating it again is fairly easy. The part that will always take a while to do is creating the list of feedback comments and/or questions for students. For more examples of good feedback comments and questions, check out the feedback pages of the Classroom Challenge lessons from the Mathematics Assessment Project.

Hopefully this process will make it a bit easier to give students individual feedback in the form of comments. Let me know if you have any questions.

Formative assessment means more than just giving a quiz or an exit ticket. An assessment is only formative if the teacher (or her students) respond to the information gathered.

However coming up with an appropriate response is typically hard to do. After all, the most common finding in formative assessment is that a significant, but perhaps minority, group of students still do not understand a concept, after the teacher gave her best shot at helping students understand. No teachers save their best strategy for teaching a topic until later.

I’m working on a menu of possible responses teachers could come up with. Some of these responses depend on the nature of the formative assessment gathered, but most of them can be applied in many different contexts.

If you have other possible strategies teachers can try, please feel free to add them here or comment below.

Here’s an approach to teaching about the relationships between the different forms of the equation of a line that is based on constructivism.

1. Be clear with students what the objective for the lesson is today.
2. Give students a tool for looking at the relationships between the different forms of the equation of a line.
3. Ask them to write down what they notice and what they wonder after they have played around with the tool themselves. Circulate around the room to see what they write down so you can better make use of it in the whole group discussion.
4. Next, as a group, discuss what students notice and what students wonder about the graph, or use a different talk protocol.
5. As a group summarize what appear to be the most important observations made, and everyone (including the teacher) writes them down. If important points about these representations of a line are not brought up, either ask questions to prompt students to realize these points themselves or make a note to yourself to structure a task that will help draw out these points next time.
6. Come back to this concept multiple times in a variety of different ways over the next few weeks, and even find ways to connect to this topic through-out the rest of the year.

Here’s an approach to this same lesson based on cognitive load theory.

1. Be clear with students what the objective of the lesson is for today.
2. Give them notes on the different forms of the equation of a line and some worked examples.
3. Give students twenty or so practice problems to do themselves. Circulate around the room while students do this and give them timely, efficient, and useful feedback.
4. Quiz students on their understanding of the concept. Use this to guide your planning in subsequent lessons.
5. Review this concept with students at spaced intervals over the course of the rest of the year.

My recommendation is that if you are unclear on how either of these approaches is helpful for students, then you should try it at least once. I have in fact tried both of these approaches myself, and I’m quite clear on which approach helps students make better connections to other areas of mathematics, and which approach did not work.

Which approach is more likely to lead to an instrumental understanding of mathematics? Which approach is more likely to lead to a relational understanding of mathematics? For reference, here’s a comparison of instrumental to relational understanding.

This is a video of Magdalene Lampert taking about Ambitious Math Teaching. I’m sharing it mostly so I don’t forget where it is.

I read an important passage in Elizabeth Green’s book “How to Build a Better Teacher” and decided that I had missed something important when reading about Magdalene Lampert’s teaching. Below is a summary of some of the important features of her teaching as I see them. The first tweet is the thing that I had misinterpreted as students talking to justify their reasoning, which is similar but not exactly the same as students talking to prove their reasoning is correct.

I’m tired of having to search all over the place to find the-link-to-that-mathematics-resource-I-really-want-now-and-bookmarked-a-year-ago and so I created a spreadsheet to keep track of the various mathematics resources as I learn about them. Yes, I know I could have done this with Diigo or Delicious, but I prefer the portability and simplicity of a spreadsheet.

I’ve opened the spreadsheet up for editing and will curate it to ensure it only includes what I consider to be the highest quality resources. The spreadsheet contains the categories of websites, mobile apps, software, books, research, and organizations. If you have a suggestion for a resource you think I should include, please offer it below, or add it to the spreadsheet. Note that I have currently protected the first sheet (the list of websites) so that you can comment on it, but not edit it directly.

This is by no means complete and will continue to evolve over time as I learn about new resources.

NCTM recently asked for Grand Challenges that are ambitious but feasible, positively impacting many people, and which should capture the public interest. Here is my grand challenge:

• Develop a comprehensive, national professional development model that supports the high quality mathematics instruction they have been promoting for many years.

Here’s what I think that could look like:

• We start by norming between a fairly large team of mathematics educators a core set of high quality mathematics teaching practices are, and what they look like in a real classroom.
• We then carefully study (to ensure that the practices work) and implement these practices in model classrooms where the educators who have previously normed continue to study their practice while continuing to discuss and collaborate with the original group of educators.
• These classrooms should be substantially open to the public (perhaps through video cameras, one-way glass, etc…) so that other educators, parents, and policy makers could come and visit the classrooms.
• Once each original educator has established clear evidence (from evidence of student learning) that they are able to consistently and reliably use the set of core practices (along with whatever other practices they have developed), they start norming their practices with another group of educators.
• This process continues until we have created a substantially similar core set of instructional practices that fairly large group of mathematics teachers consistently use.
• Two of the core practices we would establish are the teacher as researcher into their own practices and the collaboration with other educators to study each others practices to see what works.

There are some other core practices that I think that every mathematics teacher should do, but the most important core practices are to study your own practice and to collaborate with others in doing the same. Once this is established, then at least when each of us is experimenting with a different practice it will be easier for us to see the connection between what we do and student learning.

Here are some other ideas I think are also worth pursuing.

• Develop teacher training models at scale where teachers spend at least six months in close apprenticeship with an experienced classroom teacher with time to reflect on their emerging practice during this time. Follow this up with at least two years of additional support.
• Support many (one in every major city) smaller TMC-like mini-conferences with the overall aim of building local communities of mathematics teachers. Continue support of these groups by creating online space for these educators to continue their conversations and share resources with each other.
• Actively support the use of online professional development to increase the number of mathematics educators connecting with each other.

Imagine you are asked to learn about something, and the only way someone can help you understand it is with words, because there are too few examples of it around to actually see it for yourself. You think you know what it is they are talking about, but you keep getting confused because your image of what it is seems so much different than what the other person is describing.

It gets worse because most of the other people you talk to haven’t really seen it before either, and are relying on a story they read about it once before in a book or occasionally on their attempts to tell the story to other people. They sometimes contradict each other, and then other people come in and start telling a totally different story. In fact you aren’t listening to just one story, but many different stories all at once.

When you were growing up the story you were told was pretty different. None of your friends or family knows this new story. In fact, you were never told this story in school or even university. You don’t even really understand why you are being asked to listen to this story because as far as you are concerned, the story you had growing up was a perfectly nice story. Why come up with a new story?

You try and tell the story yourself, but it turns out the story is so different from any stories you have ever heard that it is hard to remember all of it at the same time. You make a lot of mistakes telling the story and feel discouraged and decide you should just stick with your old story. It’s a lot easier to do, and virtually everyone you know seems to value it a lot. Gradually you stop trying to tell the story, and stick with the older story that you undersntand very well.

This description pretty much exactly summarizes a reason why I think math education is so hard to change. The narrative around the changes necessary is often just too different than people’s personal experiences of learning mathematics.