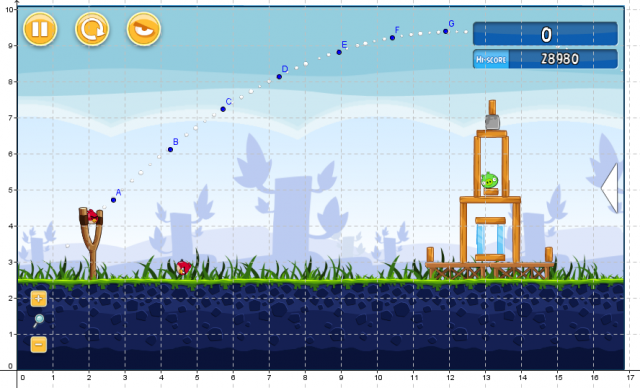
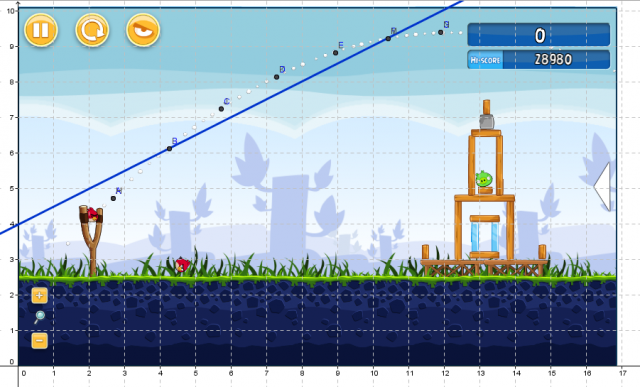
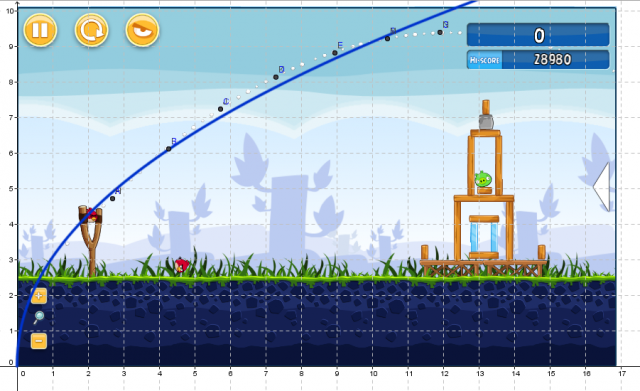
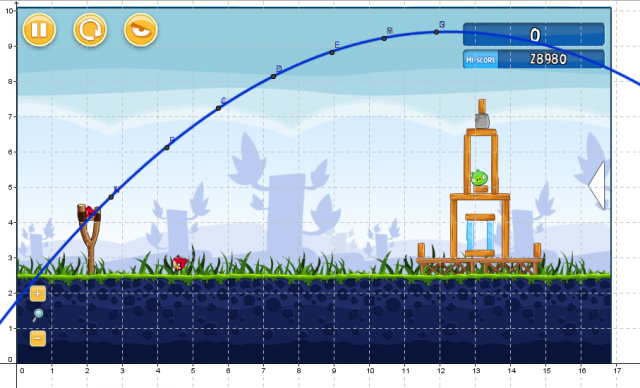
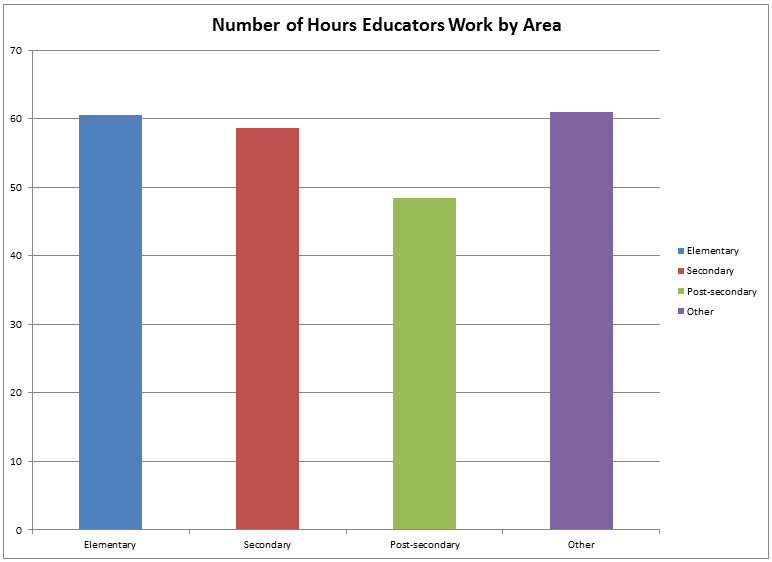
Mathematics is not medium neutral. What we call the mathematics that we can do with pencil and paper is different than what we can do with a computer and call mathematics, which is different again than the mathematics we can do with origami. The medium defines the mathematical space, in the same way that Marshall McLuhan talks about the medium being the message.
There is certainly overlap between pencil & paper mathematics and computer mathematics, but there are also differences, and more importantly, each medium has mathematical constructs which are either more difficult or even impossible to express in the other medium. In the same way that people switch between languages to express ideas that cannot easily be expressed in another language, the same is true of mathematics. It is perfectly natural that some mathematics is more easily represented in one medium, and some mathematics is more easily represented in another medium. This is the nature of mediums for communication.
Dan Meyer gives as an example of something which is challenging to create with a computer:
Use a computer to compose a clear proof that a triangle’s medians create similar triangles and send it to me for assessment.
As another example of this challenge of mathematical representations in different mediums, I offer this:
Draw the Mandelbrot set with pencil and paper.