How can a networked community could be embedded in the design of authentic learning experiences in math or science?
Part of my ETEC 533 course is to examine networked communities, such as Second Life (as an example of a multipersion world simulation), using resources such as PBS Nova Adventures (which provides the ability to hold virtual field trips), and Western’s Integrated Laboratory Network (which allows students to complete a variety of lab experiments online). What these different systems have in common is that they provide a simulation of a real-life learning experience, accessed through the internet.
One immediate question I have is, do these networked communities have any value? This question is relevant because before one can decide on the "How" one really needs to engage the "Why" question.
It is hotly debated for example whether Second Life is in fact a useful teaching tool1. Having explored Second Life myself, it seems to me that with proper preparation (read here a LOT of time) one could construct a number of simulations for this faux-world that students could explore. One could easily represent socio-dynamics and economics using Second Life, but as for Mathematical applications, I think these might be few and far between, and end up being contrived. There are a number of science communities formed within the Second Life platform, which from a cursory inspection seem to have educational value. Our instructor had us run through a tour of an astronomical observatory, and although I’ve seen better simulations of the solar system, the ability to communicate live with other students about the simulation probably makes this a valuable learning experience.
The discussion in class of the Integrated Laboratory Network (ILN) brought up some useful points. The first point, brought up by Nancy was that the fact that the lab time needed to be booked ahead of time meant she really felt like she had to be prepared. A number of other students in my class agreed with this point, and it would be interesting to see if this effect would happen in a high school settings since of course the preparation would involving learning. Another valid point, brought up by Ian, was that the simulation felt more like "following a recipe instead of doing science", suggesting that the experiment wasn’t as valuable as a result. Another student, Tris, reflected that at his school the design portion of a lab was an extremely important part of the experimental process. My thought was that the use of this equipment physically would be extremely unlikely at the high school level and that if a student created an experiment which required highly specialized equipment, an ILN might be the only way to do it.
As for the simulated field trips, one of the greatest values I can see here is the ability to "explore" a location which is otherwise inaccessible. I can imagine a time in the not-too-distance future where students would be able to book time using a highly durable robot, and explore Antarctica or Mars, both of which are places that are either extremely expensive or improbable places to visit. Already there are excellent video field trips of many places in our world which are highly fascinating and learning rich experiences. One obvious flaw with a virtual field trip is the lack of a tactile experience. Without taste, smell and touch, the experience would be sensory deprived.
Of these three examples, it seems that only Second Life has a true social learning aspect built into its design. An ILN or a virtual field trip really lacks that social context which benefits the learning for so many of our students. It will be fascinating when computer processing becomes powerful enough to allow for multiple users to experience a virtually life-like simulation of a place caught on camera only. When this happens, and if the people can communicate during the experience, then social learning affordances will be relevant to this type of learning.
Now suppose we wanted to design an actual classroom learning experience which would use one of these tools. The easiest to do this for would be the ILN, since it has been specifically designed to be an instructional aid for laboratory science. One would have students design detailed experiments, and then have a wide variety of different tools available to them to complete their experiments, through the use of the Integrated Laboratory Network. Students would have to discuss their experiments ahead of time and reflect on their experiments afterward to allow for a social context for the activity.
To use the Second Life platform effectively, I think that a simulation could be constructed for the students to access, and then students would be given free reign to experiment within the science simulation (the orbiting of the planets seems like a good example for instance) and discuss their discoveries. One would lack much control over the specific information learned by any particular student, but it could be a valuable learning experience, particularly for the students who need help visualizing three dimensional objects.
The virtual field trips would allow for hostile locations to be examined by students. For example one could use footage of an exploration of the deep sea bed and show students how even in an hostile environment, life thrives. This would make for an excellent learning opportunity in a biology classroom.
None of the resources we have been shown looks like it would be useful for a mathematics classroom without an enormous amount of preparation. One could imagine that one could show a highly specialized simulation of a concept which involves a fair bit of mathematics, but it seems to me that any such simulations would be too contrived to be useful learning activities.
It is clear that there are uses of these networked communities within education, and even within science education there are opportunities for powerful learning to occur through these communities. One doesn’t have to look very hard to find examples of things in science worth learning which are for various reasons completely inaccessible for students (imagine setting up a virtual black hole for students to look at for instance). For this reason alone, I think these network communities are worth exploring, but I think that the inclusion of community needs to be stronger in most of these online systems (Second Life excluded) as this will allow for a strengthening of the learning opportunities available.
References:
- Aldritch, C. (2006) Second Life is Not a Teaching Tool, accessed from http://learningcircuits.blogspot.com/2006/11/second-life-is-not-teaching-tool.html on March 31st, 2009.
- Cancilla, D. A., Albon, S. P. (In Press) Moving the Laboratory Online: Challenges and Options, Journal of Asynchronous Learning Networks.
There are a lot of good open source programs out there, but not many of them have direct application to a mathematics classroom the way 
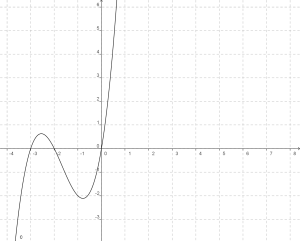There are 2 cool things I like about Geogebra. The first is that you can export your working file as a dynamic worksheet on a web page, which means you can easily make what you are working on web ready. The second feature which I use all of the time is the ability to export my current file as a picture in PNG (and a few others) format. This allows me to use Geogebra to create graphs for inclusion in my online posts, something my students and I use Geogebra for all the time.
over the domain from 0 to 2 for x. Very handy.
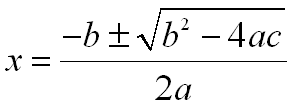One difficulty faced by any mathematics teacher who wants to present material online is formatting of their documents. Ideally, you’d like to be able to add equations to your online documents as easily as you can to Microsoft Word. Unfortunately, this is not the case.
. Fortunately on the page in question their editor allows you to modify the LaTeX using some buttons, which simplifies the process. You can also preview the result of your LaTeX to make sure it is correct. You then save the resulting preview image to your computer, and upload and insert it into your post.
A project I have done with my 9th grade students now for 4 years in a row, is to have them do some quadratic modelling. When I worked in London, I was really lucky because the students were creating trebuchets and catapults in their Design class. So we had a class where the students took their models they created in Design up to the nearest park, and we took digital footage of the trebuchets in action.