
What you teach should either have relevance in your students lives, either now or in their future, or it should be engaging. If neither of those is true, don’t teach it.
Education ∪ Math ∪ Technology

What you teach should either have relevance in your students lives, either now or in their future, or it should be engaging. If neither of those is true, don’t teach it.
I recently contacted Derek Stolp, author of Mathematics Miseducation: The Case Against a Tired Tradition and shared with him Paul Lockhart’s essay entitled "A Mathematician’s Lament." With his permission, I’m sharing his thoughts below.
Lockhart’s argument is very compelling, and I certainly share his concerns about the state of mathematics education in this country, if not the world! The traditional approach to teaching mathematics, however, is only part of a much larger problem: the widespread acceptance of the transmission model of learning (as opposed to the constructivist model). Educational practices continue to be dominated by the principle that, if I may state it baldly, children just need to be told what to know and how to think, and this is true to some extent in nearly every academic discipline. (And I believe that this authoritarian model is, in the long run, inimical to the development of democratic values and practices!) I won’t belabor these points here but I do discuss constructivism and the tool metaphor on about pages 50 – 60 in my chapter entitled “Whose Knowledge Is It?”
Despite the power of Lockhart’s argument, I do think he needs to go beyond a lamentation. When I wrote my own book, Mathematics Miseducation, my wife read the opening chapter and said that she found it to be too negative. (As a kindergarten teacher, her preference is for the positive approach.) I told her that, as a math teacher, my habit is to identify the problem and to be certain I understand its contours before trying to solve it. In subsequent sections of the book, I do try to present possible solutions that solve the problem. But the book itself does not provide enough detail for the average teacher to change her/his practice so I decided to set up a web-site with lessons that teachers could use that would be consistent with my approach. I’m not entirely happy with all of the contents of that site – I’ve had to compromise my ideals with the practical reality of the school in which I teach. My 8th graders go on to secondary schools so I have to teach them algebraic fractions and radical expressions in my algebra course, as distasteful as it is to do so. And when they ask me, “Why do we have to learn this?” I try to be honest and say something to the effect, “If it were up to me, I wouldn’t teach these things. Math education is very slow to change, and it’s stuck on 19th century practices. But you’re going on to a school that will require you to learn these things, so I’m trying to get you started in a way that will diminish the pain for you next year.”
Here’s another example of a compromise I’ve had to make: About 15 years ago, when I was chairman of the math department at Milton Academy in Massachusetts, some of my colleagues and I introduced mathematical modeling courses as alternatives to traditional symbol-manipulating abstract pre-calculus and calculus courses. We taught the same fields of concepts – in trigonometry, for example, modeling studied the rotation of a Ferris wheel and the shifting of tides whereas the traditional course found it more important to develop all those unnecessary trig identities – but at the end of the year, we devoted three weeks to SAT Math Level II review because these kids and their parents, while they loved the course, were not about to sacrifice their standardized test scores.
So here’s my point: Dr. Lockhart has, in his paper, identified the problem very clearly. His next step is to offer an alternative that will remain true to his ideals but that will realistically fit in a more traditional environment. He does suggest a way:
“So how do we teach our students to do mathematics? By choosing engaging and natural problems suitable to their tastes, personalities, and level of experience. By giving them time to make discoveries and formulate conjectures. By helping them to refine their arguments and creating an atmosphere of healthy and vibrant mathematical criticism. By being flexible and open to sudden changes in direction to which their curiosity may lead. In short, by having an honest intellectual relationship with our students and our subject.”
But how could he be more specific for those teachers who are sympathetic to his arguments but need guidance and resources? One way he could do that is to create a web-site with problems he has posed, indicating the levels at which they are appropriate. He’s been teaching high school, I gather, so he must be developing some materials. (I would love to see the day when textbook publishers are out of business because real teachers put their materials on-line for other teachers to access for free.) This, of course, will require considerable compromise on his part, compromise that he might feel destroys his objective. But I see no alternative.
The reality is that our schools are captive to an authoritarian trend to top-down standardization, and neither political party believes in a democratic form of education – Arnie Duncan has merely put old wine in new bottles – because we don’t really have a progressive political party – just a Republican Party and a Republican Lite Party. Progressives in education will have to chip away at the edges a little at a time and that will require distasteful compromises.
I’ve been asked to look at the Upper Elementary (Grades 4 – 6) math program at our school, and I’ve recommended using a program called Everyday Math. While I am not a textbook fan and haven’t used any for more than fifteen years, these teachers are teaching every subject and they need a resource. Here are excerpts from my memo to them:
"I know that it’s normal for every teacher to think about what needs to be accomplished by the end of the year so that his/her students will be ready for the next level and, since the kids are coming up to middle school, I thought I should let you know what skills, habits, and understandings I’d love to see among the incoming children. At http://www.maa.org/devlin/LockhartsLament.pdf is a paper entitled A Mathematician’s Lament which has been expanded into a book. This article was sent to me just this week from a math teacher in Vancouver and, while you’re certainly welcome to read the whole thing, I’d encourage you to read at least the first two or three pages – it will give you a flavor for the author’s point of view and, since I agree with him in principle, mine as well. His goals are lofty if unrealistic in today’s educational context, but they are certainly worth keeping in the back of one’s mind.
So, here are some of the important qualities that I would hope each child would possess coming into the middle school:
– Enjoys doing math
– Feels confident about approaching new problems
– Likes to make conjectures about patterns and is comfortable about being wrong
– Can talk about methods of solution with classmates
– Is resourceful about finding a solution method if he/she had learned it before and has forgotten it.
You’ll notice that there’s nothing here about knowing his/her times tables or knowing how to add fractions. Naturally, I’d love for each child to know these things but, to me, they are secondary. If a child has to take timed quizzes on multiplication facts (mad minutes?) or do pages of drills on adding fractions to master these, then the price is too high because it hampers the development of the qualities that I believe to be more important. So, that’s my bias. In the process of teaching math, we want to expose them to the many concepts and skills in your curriculum but, if they aren’t ready to master some of them, that’s fine – they’ll master them later.
One thing to keep in mind about the program: it’s not important for each and every child to achieve mastery before moving on. Some will, some won’t, and those who won’t will have chances later on to achieve it. And if they don’t by the seventh grade, don’t worry about it – I’ll address it then, and maybe they still won’t achieve mastery. (Several years ago, I had a conversation with a parent at Milton who was also a child psychologist working at MIT’s Department of Brain and Cognitive Sciences and she told me that several of her colleagues used to joke about the fact that they had never been able to learn their times tables. Somehow, these people managed to get by!!) The program has a good balance between skills practice and review on the one hand, and investigations and games, on the other. And I would lean heavily in the direction of investigations and games."
This memo to my colleagues reflects the kinds of compromises that I believe are necessary; the road to progressive education can be walked only one step at a time. Anyway, these are my thoughts regarding Dr. Lockhart’s excellent article, and thanks for allowing me to share them with you.
Derek Stolp
Is this mathematics?
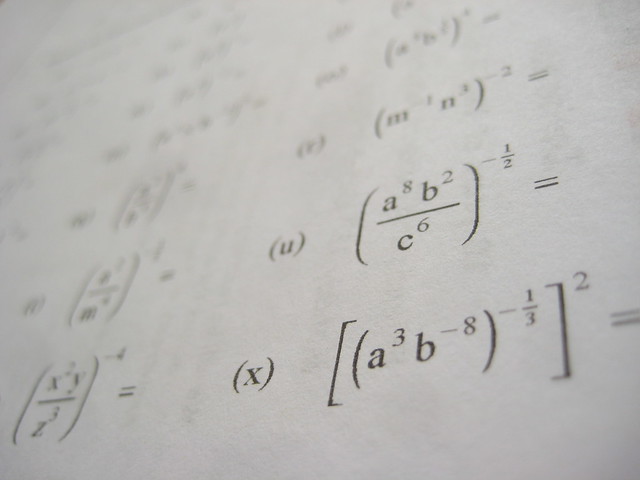
Join us this coming Thursday, at noon Pacific time, Richard DeMerchant, and I will be hosting an online book study of "A Mathematician’s Lament" which is an absolute must read for all mathematics educators. One of the questions we will try to answer is the one above, and you can ask more questions either on this blog post, or on Richard’s original announcement.
‘I don’t see how it’s doing society any good to have its members walking around with vague memories of algebraic formulas and geometric diagrams, and clear memories of hating them.’ (emphasis mine) ~ Paul Lockhart, A Mathematician’s Lament, p33
Paul Lockhart, first in his essay, and then in the extended version of his argument in his book, makes the case that current practices in mathematics education are fundamentally flawed because students spend much time learning the language of mathematics, without ever getting to actually do mathematics. I recommend reading his work in full, even if you are unable to participate in the upcoming book study.
Our plan is to work through his book and discuss the ideas in it, using quotes from the book as ways to kick-start conversation. Here’s my favourite quote from his book. What do you think of it?
‘Everyone knows that something is wrong. The politicians say, “We need higher standards.” The schools say, “We need more money and equipment.” Educators say one thing, and teachers say another. They are all wrong. The only people who understand what is going on are the ones most often blamed and least often heard: the students. They say, “Math class is stupid and boring,” and they are right.’ ~ Paul Lockhart, A Mathematician’s Lament, p21
I had an idea for a proposal which I put in the TED-ED forums for a TED talk on Math in the Real World. Here’s my presentation, notes are below the presentation.
Presentation notes:
Slide 1:
Hi all. My name is David Wees, and I’m a learning specialist for technology and mathematics teacher for Stratford Hall, in Vancouver, BC.
Slide 2:
I want to first state that I don’t believe that doing mathematics is the same as doing computations or following algorithms.
Many math teachers seem to be stuck on the notion that teaching kids how to do computations out of context is the same as learning how to do mathematics.
Slide 3:
So what exactly is a mathematician, and what is mathematical thinking?
Mathematicians think. A lot. They spend much more time thinking about problems than doing computations to solve those problems.
Slide 4:
A mathematician is someone who problem solves using mathematics as their tool.
Slide 5:
As proof that change in how we teach mathematics is necessary, we can look at the overall numeracy of our society. Numeracy levels in Canada are pretty abysmal, despite years and years of formal mathematics instruction occurring in schools.
It is a badge of honor in our society to admit that you are bad at mathematics. Almost no one would admit that they are illiterate, why do so many people celebrate their lack of numeracy?
Perhaps it’s time to try something new?
Slide 6:
The problem, I see, with most mathematics instruction, is that we start by choosing the mathematics curriculum we want covered, and then find problems to suit this curriculum.
The flaw with this plan is that choosing a compelling problem to fit a particular area of mathematics is really difficult, and many math teachers don’t even try.
As a result, much of mathematics instruction lacks motivation in the eyes of the learner.
Slide 7:
Here’s the crux of my argument. We’ve had curriculum which is mostly unrelated to experiences in kid’s lives for multiple generations which has only compounded the problem.
Slide 8:
What I suggest instead is that we look at the world, and we find problems kids find compelling, and then we tease out the mathematics which is relevant to those problems. This is more difficult for math teachers to do, but will result in kids never asking the question, "Why do we need to know this."
Note that we can teach most of what we teach now to a motivated kid in a few years, rather than spreading it over all 12 years, so this way of exploring mathematics shouldn’t stop kids who are really interested in mathematics from exploring it further.
Slide 9:
It is clear that our world has some deep mathematical structures. Which of those structures do we share with our students? Why isn’t more of the world we live in shared throught the lens of mathematics? If mathematics truly is the language of the universe, our current approach has kids learn some of the vocabulary, but never construct any sentences.
Slide 10:
Trees for example have a fractal structure which is worth investigating. It is not hard to see that there is a mathematical formula of some kind which helps determine tree growth, but we can also see the idea of replication errors, and environmental factors that play a role as well. It also means that kids get a better connection between nature and the mathematics they learn.
Slide 11:
Dan Meyer suggests finding "real" examples, rather than pseudo-context is key to developing student understanding of the world. The questions about the world have to be real, and from the students. The textbooks we use today include lots of "word" problems but for what purpose? Most of the textbook word problems are too poorly constructed to be obvious representations of the world, so why bother? What purpose does exposing kids to a bunch of pretend problems serve?
Slide 12:
Outside of our own world, the whole universe has a strong mathematical structure on a large scale.
How often is this mathematical structure shared with students?
Slide 13:
Or the relationship between this fractal and the previous picture of the galaxy?
Fractals and chaos theory are an important part of our world, mathematically speaking, yet neither one sees much "playing time" in our curriculum.
Slide 14:
This is a complex project I’m working on where I am attempting to model mathematically the transfer of information in a classroom, and hence compare a didactic classroom to a cooperative learning classroom.
It’s not near done yet, so I can’t share any results, but if I do manage to complete it, the project will involve percentages, probability, graph theory, statistical distributions, geometry, Cartesian coordinates, and algorithms.
Slide 15:
Flash card apps and other ways to memorize computations and algorithms aren’t going to improve our problems with numeracy. In fact, I don’t think these are really examples of technology at all, since they do nothing new. If you are going to use technology in your teaching, you should at least be using it effectively. Graphing programs, computer assisted algebra and calculus, multimedia to emphasize patterns, all of these are much more effective uses of technology than the current generation of apps for education.
Slide 16:
To summarize my argument so far. Most people lack sufficient numeracy skills for our complex world. Our mathematics instruction really hasn’t changed in most schools for decades. Perhaps it’s time for a change? I’d recommend a focus on relevance to the real world, rather than a hierarchy of algorithms.
Slide 17:
First, put aside that useless textbook with all of the prepackaged problems.
Start by finding an interesting problem that your students find compelling and look at the mathematics involved in that problem.
Better yet, turn your kids into investigators and have them find the problems and bring them to class. Finding interesting mathematics problems isn’t hard.
Don’t worry about that test so much. If your kids can solve real problems, and those problems are in some way related to your curriculum, they will do fine on the tests.
It would be nice if we could dump our current curriculum and replace it with something more aligned to the world views of our students, but that’s not really possible, so in the transistionary stage, we should find ways to include more of what kids experience in your teaching. Don’t be so afraid to experiment, if even a few of your kids recognize math outside of your classroom, you’ve done the world a huge service.
Slides 18 through 21:
So what does this look like? I did a project with my students last year where we explored the cost of owning a cell phone, based on the number of minutes used.
First we graphed the initial cost to join a cell phone plan, and then we graphed the cost of the cell phone plan. This got us talking about graphs, equations of lines, horizontal lines, and slope. As we went through the unit, I introduced the mathematics in pieces as the students needed more to explain the problem. For example, when students asked how we could find out exactly where the two lines met, we did a couple of lessons on algebra.
Then we recognized the optimal solution was actually the green line. We ignored the negative numbers, since they didn’t represent real values, and we focused on the part of the graph which was actually our solution to the problem. We discussed domain and range, within the context of a problem the kids understand. Notice also that our solution wasn’t a single number.
Finally, we needed to tidy up our solution so that we only represented what was actually the solution the problem. Clearly, without labels on the axis, the graph of our solution to the "what is the cheapest cell phone plan" didn’t make a lot of sense. I had the kids keep the first steps, so they can talk about their solution and communicate the reasoning they went to solve the problem.
Slide 22:
There are lots of other examples like this one of real things kids want to know that involve challenging mathematics. We don’t need to dumb down the curriculum for students, we need to reenvision it. If we had a curriculum which emphasized the purpose of mathematics much more, I think we’d see a change in a single generation of students.
Slide 23:
Here’s my contact information and the license for this presentation.
Karen Cheng demonstrates fairly convincingly that music and mathematics are linked. This video is definitely worth watching.
How could this be incorporated into the classroom? Any ideas?
This is a great video from the Alberta Ministry of Education. I definitely see it as explaining the purpose of mathematics in a way that kids can understand. I also think it gives mathematics educators something to think about when they watch it. Have they done enough to embed what they are teaching in contexts which are recognizable and important to their students?
I saw on the TED blog that they were accepting applications to do a TED talk in May in Long Beach, so I thought that it was worth trying to create a video application. This isn’t the most amount outstanding video I’ve created, but give me a break, I had limited time. 🙂
Here’s an idea: How about each of your students creates their own TED-style 1 minute video to talk about their big idea?
During the Digital Learning conference this year, I ran a workshop on "Multimedia in the Mathematics Classroom" (warning large file) which was a huge hit. I started by giving a presenting giving answers to why one would want to use multimedia in math, what does it look like, and what tools I use to actually construct the multimedia with students.
I started the second part of the workshop and gave the participants a chance to escape if they did not feel like participating. I handed out Flip cameras, and gave the very lose instructions, "Create a math video word problem." Some people left the session right away, but about 20 people stayed and worked on videos, while I circulated around the room and helped trouble-shoot.
Here are three of the videos created by the participants in about 40 minutes. A fourth video was created by another group but due to technical issues, we just shared it during the session.
(Note: If you are in one of these videos, and uncomfortable being shared online, let me know via the contact form, and I’ll take down the video.)
Here are some tools which I’ve either used (or explored) for mathematics education. They aren’t all open source, but they are all extremely useful, and they are all free to use (free as in free beer, some of them are also free as in free speech).

This program lets you explore algebra and geometry, much like it’s proprietary cousin, Geometer’s Sketchpad. Having used both, I actually prefer Geogebra because I find it to be more flexible and easier to use. It will run on many different platforms including Windows, Mac, Linux, Android, and iOS.
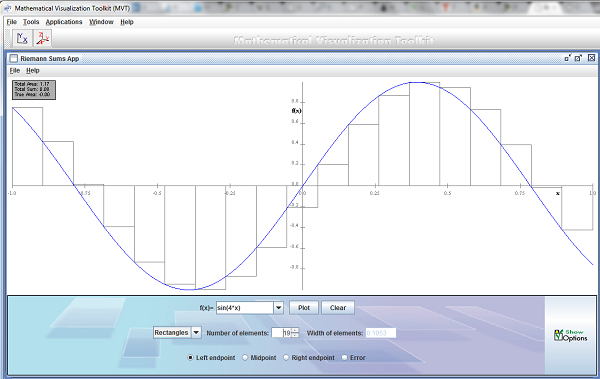
The Mathematics Visualization Toolkit is exactly that, a program which lets you visualize mathematics. You can use it to build complex visualizations, or you can use the visualizations which are already included (which are awesome by themselves). You can either use the web start version of the toolkit, or download an offline installer.
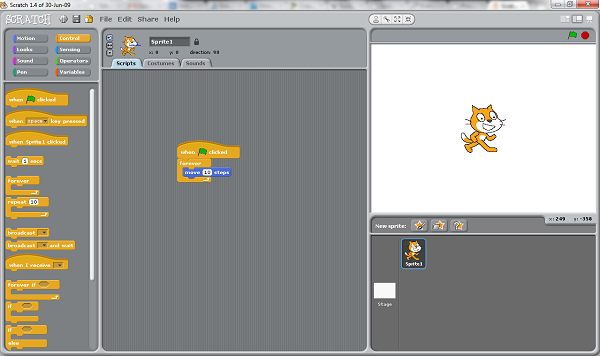
Scratch is an excellent program for learning programming but also mathematics like variables, sequences, Cartesian coordinates, and other useful mathematical concepts. Developed at MIT, it is a free download and includes a strong user community to seek help, and see what else can be done with the program.
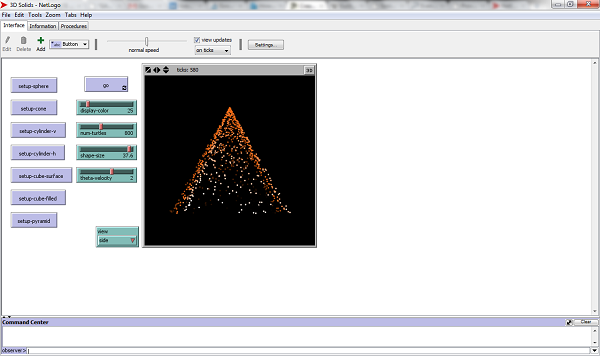
Netlogo is “a multi-agent programming modelling environment” (According to the Netlogo website). It comes with hundreds of models for all areas of science and mathematics preprogrammed. It is a free download and will work on any computer which has Java 5 or later installed.

Audacity is an open source audio editor and recorder. One example use in mathematics is to record a bouncing ball, and use the visual data from audacities recording to turn this into a graph of bounce versus time between bounces. You can also use it so students can record 60 second podcasts explaining some aspect of mathematics.
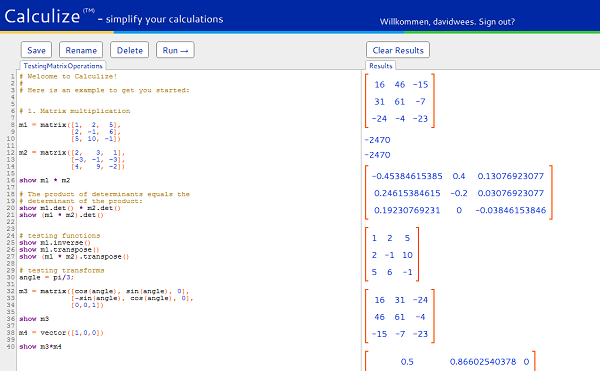
Calculize is a free (currently) web app which lets students perform mathematical computations using a reasonably simple programming language.
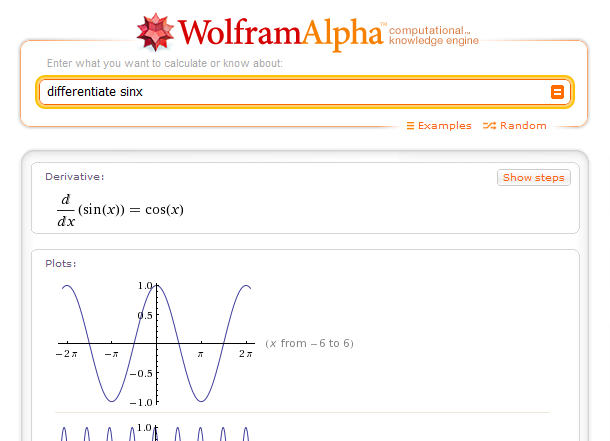
Wolfram Alpha is a computational engine built on top of the Mathematica architecture. It is amazingly powerful, and turns some homework assignments into a breeze. Recommendation: change your homework assignments, or do away with them all together.
Desmos
This is a free online graphing calculator. It emulates a lot of the functionality of a typical graphing calculator but with a much easier to follow user interface and without much of the non-graphing functionality of a graphing calculator. It is easy to create graphs, and then share those graphs with other people. It is also currently in development, so it is still improving over time with new features being added every couple of months.
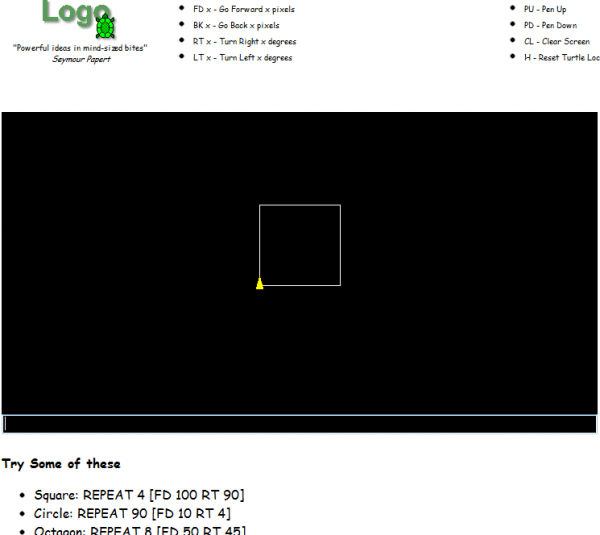
This Logo emulator lets students play with the classic programming environment Logo, built for kids by Seymour Papert and his colleagues at MIT, all online. It requires Java, but should run on most computers (sorry, no iPads…).

Google Earth is free (but proprietary) software that allows students to explore the world in 3d. One could use it for GIS applications, or even to explore the relationship between our 2d mapping system (longitude/latitude) and 3d space.

Google Sketchup (another free, but proprietary program) that allows students to create highly complex (or very simple, if they prefer) models. I’ve used it to have students construct their “ideal” school, and then from this model, they calculate the cost to build their school.

Screenr is a free (for up to 5 minute recordings) screen-casting (think record your screen as a video) software. Some possible uses of it are for students to use it to create video tutorials, record their process of solving a problem, or create their own video word problems. Another alternative for screen-casting is Jing, but it publishes to a format which is harder to share in the free version.
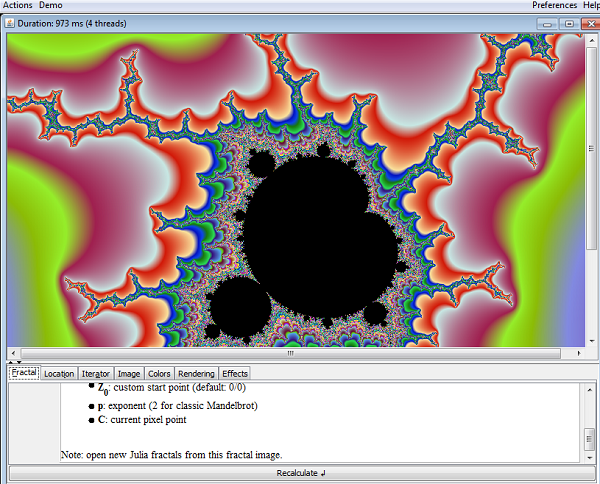
Endlos is an open source fractal generator which I’ve found runs very fast. It runs in Java, so it should run on any computer capable of supporting Java. The ability to experiment with, and explore fractals is a very interesting thing for students to do, but very tedious to do by hand…
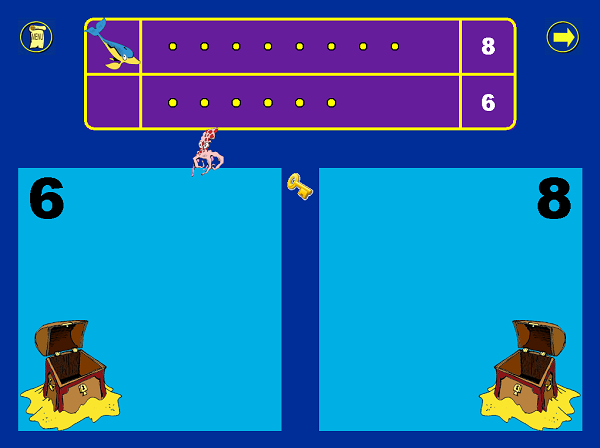
The Number Race is an open source program intended to help students who have dyscalculia develop their number sense. It has many levels of difficulty, and runs in Java, which means it should run on a wide variety of computers.
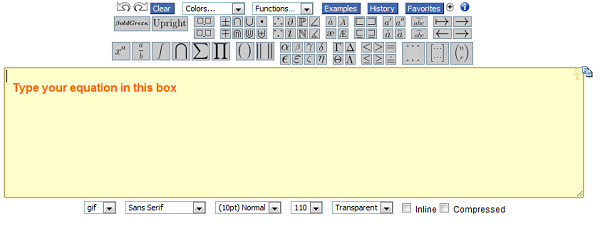
This free to use online equation editor could be a nice way for students (and teachers potentially) to construct equation images for use in a website.

Eigenmath is an open source program for symbolic manipulation in math. It runs either in Windows or on a Mac. Some examples of what it can do are shown above.
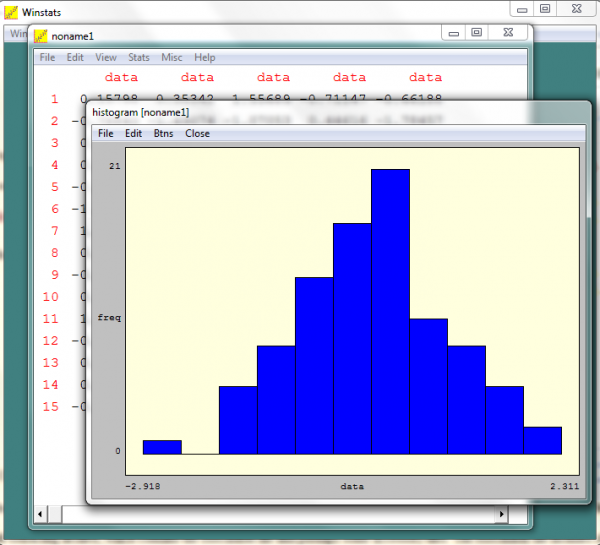
These 9 free programs cover a wide range of different types of mathematics. Above is the popular statistics calculation and visualization program included in the package.
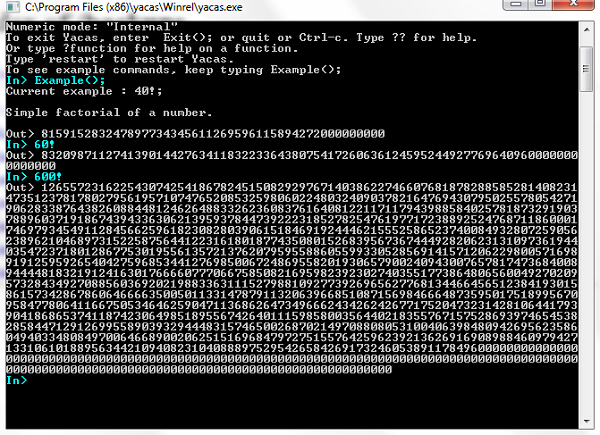
Yacas (Yet Another Computer Algebra System) is a command line program which allows for the symbolic manipulation and calculation of mathematical expressions. One thing I like about it is that it calculated 600! in a fraction of a second, so it is very fast (an aside, ever wondered what 6000! factorial is?)
Free CAS programs
Update: Just found an open source implementation of LOGO (as described in Seymour Papert’s Mindstorms) here: http://www.softronix.com/logo.html
Other free programs which I have used either for constructing mathematical diagrams/simulations or with students in some way include:
The Gimp, Programmer’s Notepad, Flex Builder (free with an education license), Open Simulator, VLC PLayer,
Wolfram Demonstrations (requires a free browser plugin), and Project Euler.
You might find these programs as useful alternatives to the “free apps” which “help” students memorize formulas & algorithms. For an enormous list of other free programs see this helpful list.
What other free programs for mathematics education do you use with or for your students?
This graph, taken from Coca Cola’s Water stewardship page, presents a very misleading picture on how effectively Coca Cola has improved their water efficiency.

This graph for me highlights an important reason that we need to teach critical analysis of graphs and statistics. Do you see the problem with the graph? (Hint: check the scale of the graph).