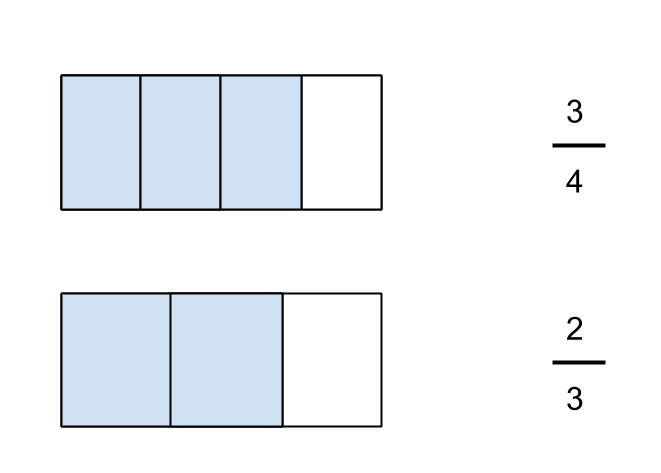
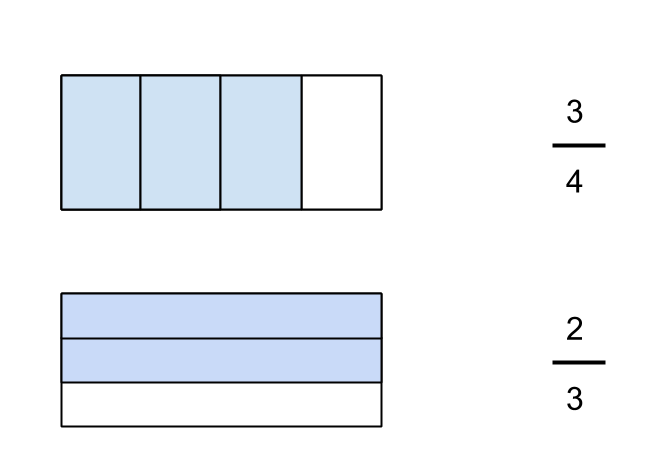
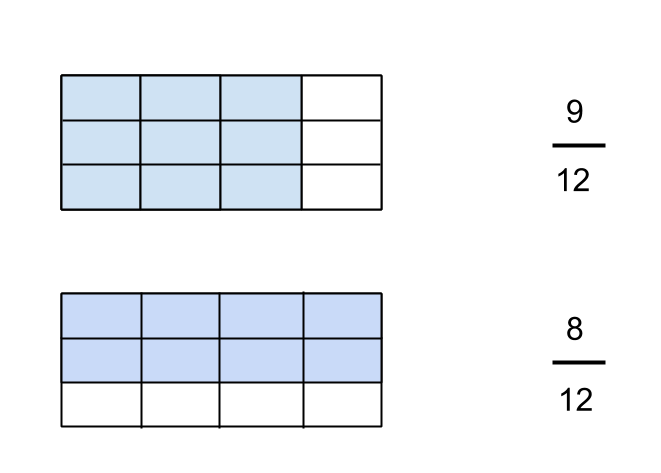
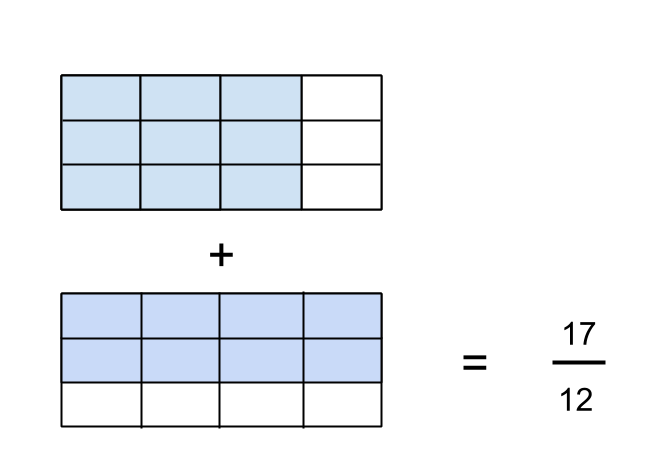
PARCC recently released some sample computer-based test items for ELA and high school mathematics, so I thought I would check them out since NY state is still officially planning (eventually?) to use the PARCC assessments.
First, some kudoes to the team that created these assessment questions themselves. In general I found that the questions were looking for evidence of mathematical reasoning, and would be difficult to game with classroom test-preparation. What I think is missing is an opportunity for students to demonstrate the complete range of what it means to do mathematics, including asking questions themselves that they answer, but for an assessment with this function, this seems much better than the current generation of standardized tests.
If you want to stop reading this and preview the questions yourself, feel free to do so (if you are only interested in looking at the sample math questions, you’ll have to skip through the sample ELA questions).
Here’s my preliminary thoughts from attempting the first few problems myself.
-
Use of space is critical. The first assessment question does not do this very well. Look at the video below that explains my reasoning on this.
-
The second question has two issues, one of which is really very minor, the other of which is something PARCC should make an effort to fix.
I’m okay with questions that use approximate models for mathematics, but it might be at least worth noting to students that these models are approximations.
Taking a test on a computer is already extremely distracting as compared to taking a test on pencil and paper. Given that there is research that shows that people generally read slower and with less understanding on a computer, PARCC should make an effort to mitigate the platform issues as much as possible. Imagine if your work flickered in and out of existence while you were writing it down on paper?
-
I put the wording for the third question through a reading level estimation calculator, and it estimated that the reading level was grade 10. While it is reasonable to expect a certain amount of competence from students in this respect, we have to be careful that our assessments of the mathematical thinking of students aren’t actually measuring whether or not they can read the prompts in our assessment.
-
Question 5 assumes a certain amount of cultural knowledge, specifically knowledge of playing golf. Having worked with students who do not have the this sport in their cultural background, I found assessment items like this frustrating. Usually, the questions are doable without the cultural knowledge, but imagine you are a student who comes across a question that contains an idea with which you know nothing. Regardless of whether or not the knowledge is required to do the mathematics of the problem, it impacts student confidence and therefore their performance.
-
The sixth question assumes that students have some minor technical knowledge, which I would classify in the same genre as my fourth point; students with a minimal technical background may struggle with the mechanics of this task. This may not affect a huge number of students, but the assessment instrument should be as neutral as possible to allow the greatest number of students to interact with the mathematics of the task, not the mechanics of the task.
- The seventh question has a video. It’s probably between 4 and 10 megabytes in size. Can you imagine what this will do to your school’s bandwidth if every student in a particular grade is accessing the resource at the same time?
There are some things which I think are obvious to me about the computer based assessment that PARCC is working on.
The first is that many of these questions are still going to require actual math teachers, with some experience looking at student work, to look at. Most of these questions are not just reformated multiple choice questions (although some of them are). While this increases the per-student cost of the assessment, I do not think that there are computer programs (yet) that exist that can accurately capture and understand the full range of possible mathematical reasonings of students.
Next, some of the more adaptive and social aspects of the work Dan Meyer and company have put together, are not present in this work. This assessment is intended to capture what students think now, rather than what students are able to do once given more information. This is still an assessment of the content students have learned, and does not appear to do an ideal job of making sense of how students make sense of problems and persevere in solving them, attend to precision, or any of the other standards for math practice (SMP). While it is clear to me that students will have to use these standards when doing this assessment, I do not see how anyone looking at the resulting student work is going to be able to say with any accuracy what is evidence of each of the SMP.
Unfortunately, unless the standards for math practice get captured somehow by an assessment (a goal of ours during next year with our project is to make an attempt to do this systematically), it is unlikely that teachers will use them.