Month: December 2018 (page 1 of 1)

I have been to perhaps a dozen national conferences and to two dozen or so regional conferences across the United States and Canada. With the exception of one or two of these conferences, I regret having ever attended.

My regret stems not from finding the conferences uninteresting or not enjoying meeting people face to face that I had only ever met previously online, my regret stems from the fact that I think these conferences are fundamentally immoral when our world is in crisis.

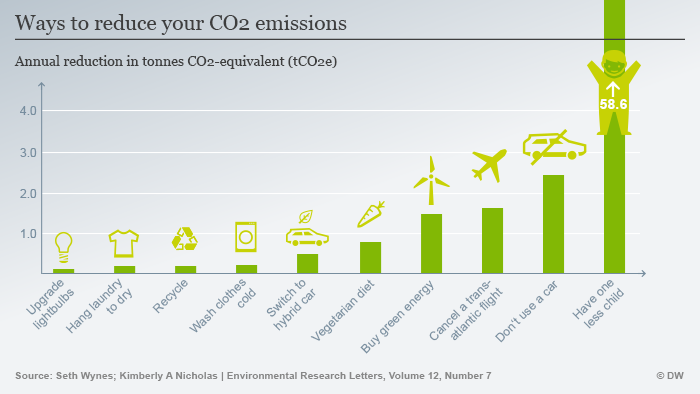
Conferences that draw people from all over a country or all over the world require participants to fly to a single destination. This results in thousands of people flying to destinations whom otherwise would not be flying. Unfortunately, flying in an airplane carries with it a huge carbon footprint. One flight across a continent or across the Atlantic has roughly the same carbon footprint as using a car for an entire year.

Here is an aggregated list of conferences across the United States. I counted 1374 conferences occurring next year, each of which may have many hundreds to thousands of participants. That’s potentially millions of flights each year for people to attend these conferences.

Maybe these conferences would be worth their carbon footprint if people learned something significant from them that changed their practice. But my experience is that this is not true. In most cases, I suspect that if a few people took two days off from work and read the same good book about teaching and then planned together based on that book, they’d get as much (or more!) out of those two days than they learn from attending 10 different scatter-shot presentations. Sessions are just not typically long enough to result in tangible learning and presenters often just don’t know the actual audience of teachers they end up with well enough to plan a session that meets those teachers’ varied needs.

It’s true that once in a while I’ve attended sessions that really made me think. A few years ago, I attended the NCSM and NCTM conferences back to back, focusing only on sessions on instructional routines, only attending sessions by a group of people who worked closely with Magdalene Lampert on these routines. That was a hugely valuable conference for me! But 1 hugely valuable conference out of the 18 or so I have attended does not justify the environmental cost of these conferences.

I think that we might be able to replace national conferences with the following and to some degree, this may produce similar learning for participants:

• Virtual conferences: Sessions are run via web conferencing software. These are ideal replacements for non-interactive (or minimally interactive) presentations that dominate most conferences.
• Book study groups: Grab 2+ friends and take two days off from work. Everyone reads the same book on day 1, on day 2, everyone convenes to first describe what things they learned and then make plans to implement some of the suggestions.
• Run smaller regional conferences: I know everyone wants to see Fawn Nguyen, Jo Boaler, or Dan Meyer speak at conferences, but I believe there is lots of local expertise in most parts of the world that could be drawn upon instead.

This year I cancelled my presentations at the NCTM annual conference, the NCTM regional conference in Seattle, and CMC South in Palm Springs. I went to one conference that I could drive to up at Whistler, the Northwest Math conference (it was really good). I do not intend to submit proposals to conferences in the future that require me to fly to the conference.

Geometric constructions are amongst my favourite things to teach in Geometry. Why? I see each geometric construction as a puzzle to be solved and I love watching children solve puzzles and share their solutions to those puzzles.

Puzzle #1: Given a line segment, draw a circle with its radius as the line segment.

Many constructions build on earlier constructions so that as students figure out how to do earlier constructions, they build the pieces they need to figure out more complex constructions. Further, more complex constructions embed all sorts of opportunities for practicing earlier constructions.

Puzzle #2: Draw another line segment with the same length as the given line segment with an endpoint on either A or B.

The invention of dynamic geometry software, like Geogebra, means that students can learn these earlier constructions without their early challenges using a compass and straightedge interfering with their ability to learn the mathematical ideas behind the constructions.

Puzzle #5: Draw a line segment that is exactly three times the length of the given line segment.

It is super helpful for students to have their prior work with constructions visible for themselves as examples to work from, and so once students have figured out how to do a construction with the digital tool, I have them transfer their construction to paper (ideally in their notebooks for reference) so they can access it later.

Puzzle #10: Draw three overlapping circles on the same line such that two of the circles have their centers on the middle circle.

Another advantage of the digital geometry tools is that you can provide partial constructions for students. This way students can work on the part of the construction that is new. This doesn’t give students practice with the earlier part of the construction but it is a subtle way to give hints to students for particularly complex constructions.

Puzzle #11: Use the circle below to help you draw a regular six-sided shape (regular hexagon).

When a student shares their constructions with the class, I usually call up a volunteer that is not that student to come up to the front of the room and perform the construction, following the verbal instructions from the first student. This means that the pace of the construction is likely to better match the pace other students can follow or copy the construction which leads to more students understanding the construction. After the construction is complete, I can ask another student to restate the instructions while I annotate important features of the construction.

Puzzle #17: Construct an octagon (regular 8 sided shape).

The last few constructions, I provide the least amount of support for students since a goal of mine is to see if students can do these constructions independently. However, note that in the instructions for the constructions, I try to make sure that the language of the constructions isn’t a barrier for my students.

Constructions #1 through #17 are available in this Geogebra book and a paper copy of these instructions is available as Lesson 2 of this Core Resource.

Let me know if you have any questions and please share other ideas you have about introducing students to constructions.

Great teaching is more than putting good tasks in front of students because a good task enacted with terrible pedagogy is still terrible teaching. While I think hardly any teachers are terrible, every teacher can be better than they are.

I see a lot of sharing of tasks, games, and activities via Twitter and blogs, but I see much less sharing of pedagogical strategies teachers would use with those tasks, games, and activities, which means a lot of people are losing potential opportunities to learn about pedagogy.

Often people share routines like Which One Doesn’t Belong or Connecting Representations which on the surface look like pedagogical strategies, but while the names themselves are somewhat descriptive, they aren’t sufficient to understand the routines they describe.

That’s part of the reason we created videos of the two main instructional routines embedded in our curriculum, Contemplate then Calculate and Connecting Representations.

Here is a (compressed) video of Kit Golan enacting Connecting Representations with his 6th grade students.

We also created slides, a pre-planner, a lesson plan, and a description of the routine to go along with these videos.

A new project we are working on is to share the instructional components that make up the routines. Here is a video showing different talk moves that can be used by teachers, either within the routines or whenever they are needed.

Here is another video showing Kit that focuses on the annotation he did while another student restated the strategy of another student, showing that these different instructional strategies can be used together and towards specific instructional goals.

It is important that explanations in the math classroom are clear and complete so that all students can follow the mathematical arguments presented. Here is one of our teachers describing how she supported students in creating clear mathematical arguments for each other to follow.

Are videos like these helpful? Would more videos sharing some of these strategies be helpful (if so, which)? And can we share more math pedagogy with each other?

A friend of mine has been fostering a child that has been diagnosed with both autism and cerebral palsy. They have seen him grow from a child who could not talk and who had a great deal of difficulty using his body to a child who asks for help when he needs it, communicates his needs and interests with others, and who can climb up a climbing wall without difficulty.

My friend shared that they were quite shocked during recent parent-teacher interviews when they were shown her foster child’s “work” from the term. They were blissfully unaware during the first couple of months of school, during which their foster child enjoyed going to school and they believed he was also getting an education, that the he was in fact not being educated. Their biggest concern was that the work he did do, circling a few answers on 2 or 3 review worksheets each day, was not helping him progress. They wondered, what does he do all day?

Their position is that while it is true that this kid is behind, not giving him any productive work to do is not going to help him catch up. They are very worried that his needs are not being met, and I agree with them. I worry that his teacher is “meeting him where he is at” and that this means that he has little to no opportunities to grow. When this child has been supported and pushed to grow, he has responded by learning and growing immensely. The extremely low expectations that this child’s school has for him risk his future.

So what would you do if you were this foster parent?