Year: 2017 (page 1 of 2)

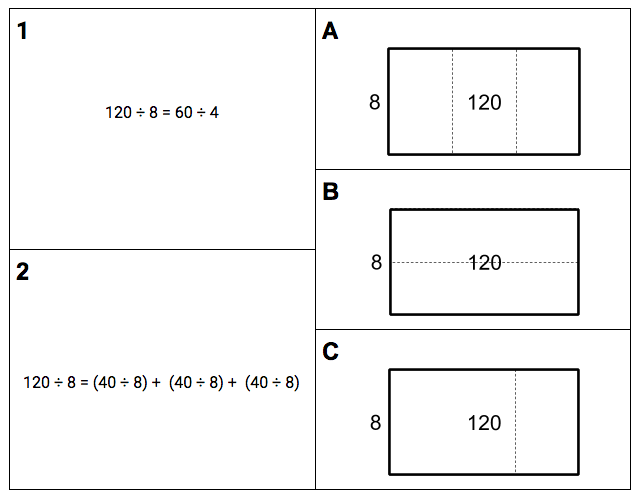
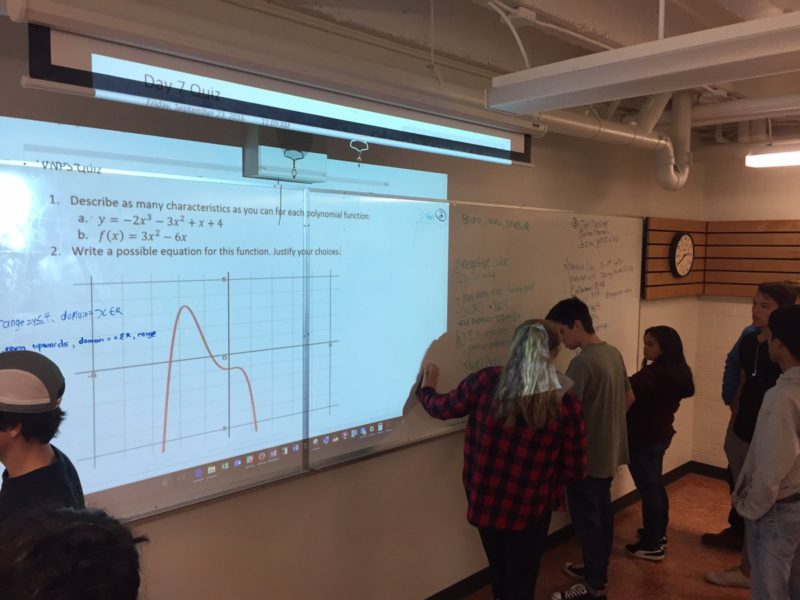
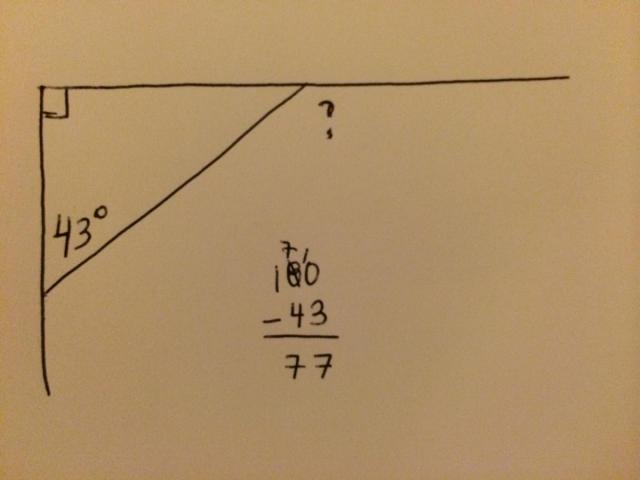A very common situation in many classrooms is that there is only one computer and it is usually attached to a projector. How can one meaningfully use technology under these circumstances?

An example of an interactive tool

Here is a strategy that may help when you want students to use an interactive tool but either have limited access to devices or do not want to waste a bunch of classroom time handing out devices.

1. Introduce the goal of using the technology to students.

We introduce the goal first so that students have some sense of what they are trying to accomplish. The goal can be somewhat vague so that it doesn’t take any of the magic out of the lesson, but ideally upon reflection students should be able to see either how they reached or did not reach the goal.

2. Have a pair of students come up to use the tool and demonstrate in front of the class.

The pair of students will problem solve with direct access to the computer. They can manipulate sliders, drag things around, etc… and use the interactive tool as designed. Everyone else works with a partner to do the same thinking and discussion about the interactive tool but without the direct access that the one pair has. The rest of the class is relying on the pair at the front of the room to manipulate the interactive tool in ways that are useful to their own learning.

This also frees the teacher up to circulate around the room and listen in on the conversations students have. This will give you some formative data on what students are thinking about during their discussions.

Note that it is best if the pair at the front of the room takes enough time to finish using the tool so that everyone in the room has sufficient time to notice relationships (if that is the goal). Therefore the pair that comes to the front of the room should be a pair of students that you can rely on to move deliberately enough that everyone has access to the range of possible things noticeable via the tool.

3. Have someone else describe their thinking.

Have someone, other than the pair of students already at the front of the room, describe relationships they noticed while the pair already at the computer manipulates the interactive tool under their direction in order to demonstrate the thinking being described. At this stage, it may be helpful to annotate or otherwise record a representation of what is being discussed so that it is clear for all students. You may decide to ask a few different students to present and you may want to select which students to present based on circulating around the room earlier.

During these presentations, you may want to use a variety of strategies to make the thinking of the pair of students clear for everyone.

4. Have students reflect on or apply what they learned.

Students should have opportunities to reflect on experiences that they have, either by trying to apply the ideas to other problems or by writing about those experiences.

Here is a good point from David – if you have a document camera you can use this same principle with anything that you have.

Yeah, provided you have some way for everyone to be able to clearly see the thing. Maybe could use with manipulatives underneath a document camera as well?

I should add this point to the blog post.

— David Wees (@davidwees) December 20, 2017

Take a look at this video of an interactive tool being manipulated so that you can experience what it is like to watch something being changed without being able to change it yourself.

(For those who are interested, the tool in the video is available here).

A while ago, I had something very similar to the following shared with me. The student was given the diagram and asked to find the measure of the angle marked with the question mark.

The student has clearly made a mistake. Why did they do it? I asked on Twitter and here are some theories:

Using stacked subtraction, how could a student subtract 43 from 180 and get 77 as answer? What are they thinking?

— David Wees (@davidwees) January 12, 2015

@davidwees My guess: they brought down the 7 (70) from after regrouping and forgot their hundred and their 40.

— Andy Mitchell (@gadfly1974) January 12, 2015

@davidwees Got the ones column right. Then crossed out the 8 and wrote 7 in the tens place instead of above. Then said "I'm done."?

— Josh Fisher (@sineof1) January 12, 2015

@davidwees Crossed out the 8 to borrow the 1 but wrote down a 1 next to the 8 instead?

— Michael Jacobs (@msbjacobs) January 12, 2015

@davidwees I think this sort of thing happens when the calculation ends up being demanding and we just default to associations w/numbers.

— Michael Pershan (@mpershan) January 12, 2015

@davidwees So 10-3=7 and then 7 is present in their memory for whatever reason (because they were just thinking about it?) so 77.

— Michael Pershan (@mpershan) January 12, 2015

@mpershan @davidwees If they "borrowed" from the 8 there's a 7 sitting there?

— Chris Robinson (@MrCBRobinson) January 12, 2015

—

@davidwees Maybe as they borrowed 1 from the 8, they wrote 1, so subtracted 4 from 11?

— Chen Mingi (@chen_mingi) January 12, 2015

@davidwees when the stu borrowed 1 from the 8, the 7 s/he wrote looked like a 1. So sloppiness.

— Steven Francis (@SFrancismath) January 15, 2015

I think all of these are possible answers. Only one of them is possibly correct for this particular student but any of them could potentially be reasons a student might do this calculation incorrectly.

But do each of them have the same instructional response? I’m not clear on that. I think we need to know more than what students did right or wrong, I think we need to know what thinking students were doing. And I think we need to know what students are thinking whether a student has done a problem correctly or incorrectly. I also think we should focus on learning, not just individual performances.

If all we know is if students go an answer right or wrong, the best instructional approach we can imagine is to essentially repeat our prior instruction, except maybe slower and louder than before. If we know more about student thinking, then we can focus on experiences that will change the information students are using to make decisions, which I think is far superior feedback to students than x’s or checks on a piece of paper or the digital equivalent via a computer.

If my theory that our responses could vary depending on different student thinking, then adaptive computerized systems have a long way to go before they are really going to meet student need. None of them currently has any hope in gaining better insight into student thinking than a teacher asking the simple question, “Can you explain to me what you did here?”

One of the ways computers are being used in math education is to provide students with online practice. There are a bunch of serious problems with most of these programs.

Here is one example from the Khan Academy (apparently at least one of the flaws outlined below no longer applies to the Khan Academy. But that same flaw still applies to IXL. And Prodigy Math. And a thousand other practice apps out there.)

Feedback is terrible or nonexistent

How does everyone feel about those online maths practice things that only let you progress if you get a streak of several completely correct in a row? #MTBoS

— David Butler (@DavidKButlerUoA) November 27, 2017

Many programs will, as David points out above, only allow a student to progress after they have gotten a certain number in a row correct. But if a student is struggling to complete an activity and the feedback to the student is terrible, how exactly are students meant to achieve the streaks necessary in order to advance?

Note: Watching a video of a concept isn’t feedback if the learner has already watched that video before. That’s information the learner already has.

Impossible to see patterns

One way that people learn math is by observing patterns in their work or solution strategies as they work on a set of problems in a row.For example, what pattern do you see if you try the following exercise:

5 x 3 = ?
4 x 3 = ?
3 x 3 = ?
2 x 3 = ?
1 x 3 = ?
0 x 3 = ?
-1 x 3 = ?
-2 x 3 = ?
-3 x 3 = ?

I’ve tried this with students and most of them notice that they are subtracting each time to find the next product, and so then they make a leap and decide that -1 x 3 must be -3.

But if an online practice program only ever shows one question at a time and the numbers for these questions are selected randomly, there will be very limited opportunity for students to notice and subsequently use any patterns that emerge.

Blocked practice

Except for a handful of studies, there is a lot of research that suggests that for most people, if the goal is to remember some mathematical idea, practicing topics in blocks will take longer than if different topics are interleaved together. Almost all of the programs out there focus on students practicing discrete topics. Caveat: I did read a study recently that suggested that for students entering a course with weak prior performance, while interleaved instruction was beneficial, interleaved practice was less effective for these students than blocked practice. Further caveat: I cannot find the link to this study.

Too easy or too hard

For some students the exercises are too easy. Sometimes this is because kids select easier problems for themselves, sometimes this is because students already know a bunch of mathematics and do not need this particular practice activity. Either way, needing to work through a streak of 5 or 10 problems just to be able to move on is ineffective for these students.

For other students the exercises are too hard. A student who really doesn’t know a particular area of mathematics doesn’t benefit from practice in that area – they need teaching or access to information.

Inappropriate medium

For many, many math problems, the best choice of a medium to work on the problem is a piece of paper. Or maybe the best choice for working on a particular problem is a programming language.

These online systems offer neither. This means students are often working in a possibly unfamiliar medium without the most useful tools available for them to work.

This also restricts the people who design questions for the system as they end up likely severely restricted as to what kinds of questions they can ask if they need the answer to the problem assessed by a computer.

It obscures information from teachers

If you are a teacher and you are using one of these online systems for your students to practice, there is usually a dashboard you can look at to see how well your students are doing with a particular exercise. But these dashboards truncate an enormous amount of information about the progress of learning and actually make it harder for you as a teacher to gather the information you need to be able to act to improve your students’ learning.

They also are likely to lead to teachers looking for students making mistakes instead of looking for student conceptions, which promotes a deficit view of students instead of treating students as sense-makers.

It can lead to bad practice

Virginia Tech has an online remedial math program where students go to sit at a terminal and watch videos on math and then take quizzes on what they learned, over and over again. There is a Facebook post where almost all of the students complain about how much they hate this mathematics class. If the online practice programs did not exist, neither would this course.

Teach to One uses a computer online practice program to inform teachers when small group instruction should occur. But in this middle to upper class neighbourhood, parents revolted and the program was scrapped. But what about districts where parents have less power?

Dan Meyer outlines the many problems with Rocketship Learning Labs, another personalized learning model, in this post.

It isn’t really mathematics

If you ask a mathematician or anyone who uses mathematics regularly what mathematics is, literally none of them will answer “it is a series of multiple choice questions or short response questions asked and answered on a computer screen.”  While practicing mathematics is a decent way to get better at what you know how to do, it isn’t really the goal of teaching students mathematics.

If answering a series of problems is the only experience of math that students have, they are likely to end up with a very limited definition of what mathematics actually is.

Note, I’m not opposed to students practicing math at all. This is obviously an example of good practice and there is plenty of research to support this claim. I’m opposed to this being the primary experience of math that students have.

Conclusion

If you can possibly avoid it, don’t use these programs. Or at least try the program yourself for a couple of hours to see what the experience is really like for students. And if you are a designer of one of these online computer practice systems, for the love of God please do a better job than the industry currently is.

There’s a list being shared of ten things that will disrupt US education and I agree with Dan Willingham.

My bold prediction: none of these 10 will disrupt education. None. https://t.co/pUAtmUOK7E

— Daniel Willingham (@DTWillingham) October 16, 2017

In no particular order, here are ten things that might actually disrupt US education.

Teachers being afforded respect as a profession by policymakers and others

You do not enact law like No Child Left Behind if you fundamentally believe that teaching is a profession. You know who primarily regulates lawyers, engineers, and doctors – that’s right, in many countries they do that themselves.

Teachers, especially elementary school teachers, having adequate time to plan

In some states elementary school teachers teach all subject areas and have a total of 45 minutes to plan AND are paid so little that many of them need second jobs.

Provide curated resources to teachers

Although increased planning time may reduce this tendency, designing ambitious curriculum is difficult and extremely time-consuming, so most teachers would benefit from curated resources that they can modify and adapt using their professional judgement. Surprisingly, many teachers have to use Pinterest and/or Google to find resources for their classroom because of a lack of curriculum resources aligned to their new state standards.

Paying teachers enough that they do not need second jobs and can afford to live in the communities that they work in

One way to make getting into teaching competitive would be to pay people enough that it makes teaching an attractive choice. It would also mean fewer people leaving the profession to find more lucrative careers and leaving vacancies, especially in harder to fill content areas.

Policies intended to improve teaching not teachers

As Jim Stigler and notes in the Teaching Gap, much of US policy is engineered at supporting individual teachers at getting better and that as soon as these teachers retire or quit, their professional knowledge leaves with them and the profession of teaching in the US remains relatively unchanged. It’s a good thing for individual teachers to get better at their practice, it is better that the professional benefits from what they learn.

Equitable funding across US schools

In some school districts, schools spend $9000 per student while a few miles away in a suburban district, schools spend $26,000 a student. While this inequity exists, resources are unevenly distributed across US education and in most cases the students who need the most support to be successful receive the least amount of funding.

Equitable access to teachers across US schools

In almost all large urban areas, it pays better to work in the suburbs than it does to work in the city. This results in teachers leaving the cities for high paying, lower stress jobs outside of the cities and in uneven amounts of teacher experience across the schools in the city.

Design school structures which are coherent and communicate across all levels of education

Imagine a system where the person who teaches teachers never sets foot in a school, the person who runs a school has no time to read research or even see their teachers teach, the person who runs research has never taught, the instructional coach who supports a teacher has their own idiosyncratic teaching style, and a teacher who has to listen to all of these people give them different advice on teaching. This is considered normal for teachers across the United States. But it does not have to be that way! It is possible to design systems where all of these people work collectively rather than individually.

End economic inequality in the United States

Income inequality in the United States is increasing and given that we know already that there exists a relationship between income and educational achievement, any shift toward more economically equitable society is likely to result in improvements in education for most students.

The end of systematic oppression of people of colour

The United States has a long dark history of oppressing people of color in various ways. One way this occurs in the US school system is that the schools attended by children of color are much more likely to be closed and/or labelled as failing than other schools. Ending this systematic oppression would transform the United States educational landscape.

My colleagues have long been frustrated sharing our work at conferences primarily because the work we do is complex and hard for people to understand thoroughly within the constraints of a conference session where we only have at most 75 minutes to work on an idea.

So we contacted the organizers of the two NCTM regional conferences and proposed a possible solution. Instead of running one session, we will run 4. Instead of 4 separate sessions, we will plan those 4 sessions to connect together. Given how closely my colleagues and I work, we were each able to be the lead speaker on a different proposal. Both the NCTM Orlando and NCTM Chicago conference organizing teams agreed to this proposal and scheduled our sessions both so they do not overlap and also sequentially as requested.

So although we have 4 separate workshops listed in the program guide, these sessions are actually one of our day-long workshops divided into four sessions. Our hope is that some participants will experience one workshop and be no worse off than before – they will still learn something even if it is not the complete picture – but that participants who attend multiple sessions will have more insight and ability to use our work.

Here is a video of Contemplate then Calculate in action, with Kaitlin Ruggiero as the teacher and some teachers from one of our courses playing the role of students.

If this teaser intrigues you, our four sessions are:

1. Experiencing Instructional Routines: 

   In this session participants will experience the same instructional routine three times with three different tasks to consider what elements of the teaching that occurs are part of the routine and what elements probably depend on the task and the students.

2. Unpacking Instructional Routines: 

   Next, participants will experience the routine again (this will give access to people for whom this is their first session) and name the parts of the routine, why those parts are helpful, and what questions they have about the routine.

3. Planning and Preparing Instructional Routines: 

   There is good evidence that a new teaching idea sticks better for participants if they have an opportunity to incorporate it into their existing teaching by planning and preparing to use the idea, so that will be the primary focus of this session. This will also connect the planning process for the instructional routines to the 5 practices for orchestrating productive mathematical discussions.

4. Rehearsing Instructional Routines: 

   There are two goals of this session. First that some participants will have an opportunity to apply what they have learned and actually practice using the instructional routine before trying it out with students. Second, rehearsal of teaching is a useful way to norm around teaching practice and to try things out in teaching in a lower pressure situation than with a group of students.

Here are the times and locations for these sessions in Orlando:

And here are the times and locations for our sessions in Chicago:

Further reading about instructional routines:

• Why instructional routines?
• Instructional Routines as Formative Assessment
• Ambitious Mathematics Curriculum

Here are some questions that I ask myself whenever I read through a mathematics curriculum:

• Does this curriculum assume that children will forget ideas over time?
• Does this curriculum provide instructional supports that increase the odds that all children have access to it?
• Does the curriculum assume all students are capable of learning and doing interesting mathematics?
• Are the connections between different mathematical ideas made explicit, both for me as a teacher, and for students who will experience the curriculum?
• Is it possible, based on the license and format of the materials, for me to extend / adapt / modify the curriculum based on student need?
• Does the material make it easier for me to use formative assessment practices each day?

If the answer to all of these questions is not yes, I don’t want to use that curriculum. A curriculum which is no more than a collection of tasks is no more useful to me than my ability to search for resources in Google.

What other questions do you ask yourself when reviewing curriculum?

There is evidence that students who have access to and understand how to use different mathematical representations of the same mathematical concepts are more successful learning mathematics than students who only have access to one representation type.

The issue is that mathematical representations are not intrinsically meaningful on their own. Some mathematical representations are completely arbitrary and for others it can be challenging to determine to what elements of the representation to pay attention.

Here is an example intended to highlight how some mathematical representations, even ones that are very familiar, are somewhat arbitrary. Check out the diagram below and ask yourself, “What is meant by each of these models for the less than, equals to, and greater than signs?”

The less than, equals to, and greater than signs are arbitrary. They are symbols to which we denote meaning and which otherwise do not contain any mathematical information without that meaning assigned.

Another issue is that students do not always attend to the critical features of a mathematical representation. For example, I have often seen a shape and a formula for calculating the area of that shape introduced together, possibly like it is shown below with a calculation of area alongside the visual.

But to what exactly in this representation do we expect students to attend? The most obvious features of the diagram of the rectangle that correspond to the area formula are the 5 and the 3. These refer to the quantities of length and width. But what is meant by the multiplication of those two quantities? How is this multiplication represented in the diagram? There is no special reason from diagrams like these that children will attend to the space occupied by the rectangle and match that to the area of the rectangle, so we need to find ways to draw their attention to this element of rectangles.

Mathematical representations have potential power to subtly introduce ideas to students as well. The number line is a good example of a representation that is often introduced early and may lead to some powerful questions by students.

What do those arrows on either side mean?
What does the space between the numbers represent?
What does going left on the number line mean?
When does the number line stop?

Each of these questions has a mathematical answer and the number line can again be used to represent this answer (warning: but not always very well).

I worked recently with a group of teachers, and we looked for shortcuts to solving the equation x + x = 116 – 84.
Here are some of their shortcuts.

But what if we tried to represent Strategy 2 and 3 on a number line? Here are a couple of different visualizations of these strategies. What information is captured differently by the different visualizations?

In our math curriculum, when introducing an area model for factoring and completing the square, we first introduce the representation itself before we do any other mathematical work using it.

Try out this applet and ask yourself, “What relationships between the visual and the expression do you notice as you change the value of a?”

In a classroom setting, we could ask students to share their answers to this prompt with a partner and then we could ask some students to share their answers with the entire class. After this, if necessary, we could add an observation from another class, so that students know to what elements of this representation to attend.

Next, after students practice writing out expressions for unaltered diagrams, we could ask students to write expression for the following altered diagrams:

In my experience, this geometric approach to completing the square results in more students in having access to the algebraic approach, and makes the name of the algebraic strategy more obvious.

Mathematical representations can offer explicit ways for students to make connections across different mathematical topics. In our Algebra I curriculum, we do not have a unit on graphing. Instead interpreting and using graphs is part of all seven units, increasing the odds students make connections in and between those units and also that students remember key ideas from the course.

To summarize:

• Don’t assume that mathematical understanding is transmitted by the representation.
• Some mathematical ideas are easier to introduce using some representations rather than others.
• Reusing a specific mathematical representation over and over again will both help students make mathematical connections and remember key concepts from the year.

On Big Mathematical Ideas, Cathy Fosnot writes:

Underlying these strategies are big ideas. Big ideas are “the central, organizing ideas of mathematics—principles that define mathematical order”(Schifter and Fosnot 1993, 35). Big ideas are deeply connected to the structures of mathematics. They are also characteristic of shifts in learners’ reasoning—shifts in perspective, in logic, in the mathematical relationships they set up. As such, they are connected to part-whole relations—to the structure of thought in general (Piaget 1977). In fact, that is why they are connected to the structures of mathematics. Through the centuries and across cultures as mathematical big ideas developed, the advances were often characterized by paradigmatic shifts in reasoning. That is because these structural shifts in thought characterize the learning process in general. Thus, these ideas are “big” because they are critical ideas in mathematics itself and because they are big leaps in the development of the structure of children’s reasoning. Some of the big ideas you will see children constructing as they work with the materials in this package are unitizing, compensation, and equivalence.

There are two pieces of evidence from cognitive science that support teaching to Big Ideas instead of teaching 180 discrete and perhaps haphazardly connected lessons.

1. It is much easier to remember ideas that are connected together in more complex schema.

This is why it takes many repetitions to remember meaningless information (like a string of randomly chosen numbers) and far fewer repetitions to remember meaningful information (like a poem).

Acronyms like SOHCAHTOA are far easier to remember than the three equations this acronym represents because the acronym provides some structure to the information to remember. The acronym allows us to chunk the information to remember into smaller, easier to manage pieces. The same principle applies to anything we want to remember.

I see Big Ideas as recursively being formed of many smaller ideas and that a Big Idea is a way of linking the smaller ideas together in the same way that the SOHCAHTOA acronym links together the words sine, cosine, tangent with opposite, adjacent, and hypotenuse.

2. It is much easier to remember information that we keep coming back to and are asked to repeatedly recall.

If I teach to Big Ideas, which may last more than a single session, the odds are greatly increased that the smaller ideas from which the Big Ideas are formed will be repeated across different learning sessions. This is critical because our brains are designed to forget information we don’t re-use and to remember information that is repeatedly helpful.

 
Suppose I want kids to remember Big Idea A, which is formed of smaller ideas A1, A2, A3, etc… and I teach this Big Idea over the course of a week. As I teach, I might ask kids to use idea A1 when working on idea A2, and then use ideas A1 and A2 while working on idea A3, all while asking kids to periodically attend to the relationships between A1, A2, and A3 as they are part of the Big Idea A itself. This means that during the course of a week, students may need to study idea A1 once, and recall idea A1 many times as they make connections to the other ideas of the week.

As the image also indicates, when teaching to Big Ideas means we can deliberately and explicitly make links between different Big Ideas, which means that across different weeks of instruction, the small ideas that make up Big Ideas can be referenced and repeated many times during the year. In our Algebra I course in our curriculum project, we don’t have a unit on graphing functions as graphing functions comes up in all seven units of Algebra I.

Here are some consequences of choosing to teach to Big Ideas instead of discrete small ideas:

1. You have to name both the Big Ideas and the small ideas from which they are formed.
2. Your curriculum can no longer be a collection of your favourite individual tasks as task selection and sequencing is far more critical.
3. Your lessons have to be designed to make the connections between big ideas explicit for children rather than implicit. A rich schema is unhelpful if it is woven invisibly into your curriculum.

Does this image represent a lesson or a task?

I’ve noticed that opinions are split on this question with some people calling the image above a task and others calling it a lesson. In my opinion, unless an image like this includes a description of how the teachers and students will interact with the image, it’s a task. (Aside: There’s too much variety in how lessons are described to have a very clear definition of lesson in this post, so I’ll have to save that for a future post, but this blog post by Annie Forest on different lesson structures is a great read).

One might be able to imagine how you would use this task with students and form a lesson plan based on a task, but without some insight into the intended use of a task there is enormous variation in how any particular task might be used.

This is not just pedantry. There is significant evidence that how one teaches matters and that there is far more to teaching than just putting tasks in front of kids. As a profession, if we are to have any hope of solving the problem of communicating nuance about teaching with each other, we should at least start with being clear about how we use some basic professional terms like task and lesson.

Here are at least six problems that often make inquiry-based lessons fail.

Some Problems

1. Students have too much information to process when attempting to solve a problem which can quickly overwhelm their working memory.
2. When given a new problem type, students do not always have all of the prerequisite knowledge necessary to approach the new problem successfully, leading them to need to make leaps of logic larger than they are able.
3. When students are sharing their ideas and strategies for solving a problem, other students are either not really listening or hearing what they want to hear rather than what is actually being said.
4. Students sometimes focus on the short-term “How do we solve this type of problem?” rather than “What mathematical principle can I generalize to be able to solve other problems?”

    
   Alternatively, students attempt to generalize and run out of working memory since they often have to hold both their solution and the generalizations from their solution simultaneously in their heads in order to generalize.

5. The goals and/or structure of inquiry-based lessons are often unclear. When students need to remember the goal of a lesson and the structure of an activity in order to be successful, they have less working memory available to actually be able to focus on the task at hand – the problem they are working on.
6. Students often use “means-end analysis” when problem solving which means they tend to focus less on what process they are using (and improving that process) and more on what answer will get them out of needing to continue problem solving.

Some solutions
Note: The solutions described below assume that your lesson structure is still inquiry-based. It may be that the best solution to whatever goal you have for the day is not to use inquiry at all, but have students study worked examples instead.

There are a variety of solutions to problems 1, 2, 4, and 6 which are all based on problem-structure and task selection.

For example, in the instructional routine Connecting Representations, the goal of any given task is not to come up with answers to problems but to name connections between two representation types. Students are focused on a small amount of information at any given time, which is given students in a deliberately staggered way in order to reduce the amount of information to process all at once. Connections between representation types are also easier to generalize than solutions to problems.

A sample Connecting Representation task

To improve the odds that students can generalize from their problem-solving experience, make generalizations a focus of any whole group discussion following the problem-solving time and have students reflect (in writing, perhaps in a regular journal) on what they learned today that they think they may be able to use in the future. Sentence prompts like “Today I learned to pay attention to … because …” can scaffold these reflections for students.

Another suggestion is to select tasks for which students can use a lot of what they already know to solve the problem and only have to make small leaps. We want to balance our students’ use of their long-term memory to aid them in solving problems with their working memory to make the small new leaps or connections necessary. A good rule of thumb is that if students need to make 3 or more small discoveries or new connections in the course of solving any particular problem, they probably won’t.

We’ve also noticed in our work that it can be helpful to distribute problem solving tasks both over time and over a group of people.

Distributing a problem solving task over time means giving out portions of the problem to learners in smaller chunks rather than all at once. For example, it can be really helpful to give students some independent time to first consider a problem on their own before working with a partner. Or you can divide a more complex problem solving task into smaller pieces so that students can “chunk” their earlier work into their later, more complex solutions. The Math Forum’s “Notice and Wonder” protocol is one example of this principle being used in practice.

Distributing a problem solving task over a group of people means giving learners deliberate access to each other as resources while they are problem solving.

In Peter Liljedahl‘s “Building Thinking Classrooms” work, this looks like students working at vertical whiteboards in small groups or with a partner, during which I have often noticed groups borrowing ideas from each other.

An example of the use of vertical nonpermanent surfaces, shared with permission from Michael Pruner.

In our work with instructional routines (with lots of help from Grace Kelemanik and Amy Lucenta) this means making problem solving sessions short and/or interrupting an unsuccessful problem solving session with whole class opportunities for students to share observations and ideas. In order to improve the odds that students actually listen to and understand each other (and solve problem #3 listed above), we have students first share a strategy/idea while we or a student points, then another student restates a strategy/idea while we either continue to point, another student points, or we annotate the strategy using color/symbols/small amounts of text. We have also found it helpful to press students to provide complete explanations, especially when there are missing details/jumps in logic in their explanations.

To get a sense of how this supports students, try watching the following two videos to see how the use of restating and annotation makes a huge difference in your own clarity around a strategy being shared.

Student sharing a strategy: no gesturing or annotation

Student sharing a strategy: with gesturing and annotation

In terms of the 5th problem with inquiry, around the goals and structures of a lesson being unclear, I’ve written extensively here about how instructional routines support students (and their teachers) in minimizing unnecessary extraneous cognitive load focused on “what am i doing next?” If you don’t have time to read that other post, tl;dr: routines free up working memory by allowing students to delegate questions about what their role is, what they are doing next, and why they are doing it, to their long-term memory.

Conclusion:

In many schools around the world, learning how to use inquiry-focused lessons in mathematics class is a focus of the school or mathematics department. However, inquiry-focused lessons come with their own set of challenges, raised above.

I have some proposed solutions to those challenges listed above, but I’d love to hear what other people are doing to tackle the same problems or what other problems people have noticed occur when they try to implement inquiry-focused lessons.