A while ago, I had something very similar to the following shared with me. The student was given the diagram and asked to find the measure of the angle marked with the question mark.
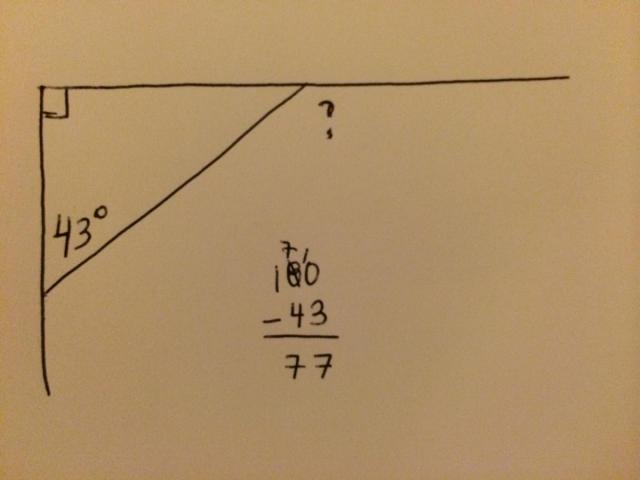
The student has clearly made a mistake. Why did they do it? I asked on Twitter and here are some theories:
Using stacked subtraction, how could a student subtract 43 from 180 and get 77 as answer? What are they thinking?
— David Wees (@davidwees) January 12, 2015
@davidwees My guess: they brought down the 7 (70) from after regrouping and forgot their hundred and their 40.
— Andy Mitchell (@gadfly1974) January 12, 2015
@davidwees Got the ones column right. Then crossed out the 8 and wrote 7 in the tens place instead of above. Then said "I'm done."?
— Josh Fisher (@sineof1) January 12, 2015
@davidwees Crossed out the 8 to borrow the 1 but wrote down a 1 next to the 8 instead?
— Michael Jacobs (@msbjacobs) January 12, 2015
@davidwees I think this sort of thing happens when the calculation ends up being demanding and we just default to associations w/numbers.
— Michael Pershan (@mpershan) January 12, 2015
@davidwees So 10-3=7 and then 7 is present in their memory for whatever reason (because they were just thinking about it?) so 77.
— Michael Pershan (@mpershan) January 12, 2015
@mpershan @davidwees If they "borrowed" from the 8 there's a 7 sitting there?
— Chris Robinson (@MrCBRobinson) January 12, 2015
—
@davidwees Maybe as they borrowed 1 from the 8, they wrote 1, so subtracted 4 from 11?
— Chen Mingi (@chen_mingi) January 12, 2015
@davidwees when the stu borrowed 1 from the 8, the 7 s/he wrote looked like a 1. So sloppiness.
— Steven Francis (@SFrancismath) January 15, 2015
I think all of these are possible answers. Only one of them is possibly correct for this particular student but any of them could potentially be reasons a student might do this calculation incorrectly.
But do each of them have the same instructional response? I’m not clear on that. I think we need to know more than what students did right or wrong, I think we need to know what thinking students were doing. And I think we need to know what students are thinking whether a student has done a problem correctly or incorrectly. I also think we should focus on learning, not just individual performances.
If all we know is if students go an answer right or wrong, the best instructional approach we can imagine is to essentially repeat our prior instruction, except maybe slower and louder than before. If we know more about student thinking, then we can focus on experiences that will change the information students are using to make decisions, which I think is far superior feedback to students than x’s or checks on a piece of paper or the digital equivalent via a computer.
If my theory that our responses could vary depending on different student thinking, then adaptive computerized systems have a long way to go before they are really going to meet student need. None of them currently has any hope in gaining better insight into student thinking than a teacher asking the simple question, “Can you explain to me what you did here?”
Tima says:
Wouldn’t it, also, be great to have your students answer that? Not just the student who made the error, but the class as a whole?
https://www.chino.k12.ca.us/cms/lib/CA01902308/Centricity/Domain/3223/learning_through_mistakes_favorite_no.pdf
December 5, 2017 — 7:59 am