Year: 2013 (page 12 of 15)

I’ve watched a lot of online webinars and presentations, and whenever there is a video of someone presenting at the front of the room, the audio quality is always horrible which makes the presentations hardly worth listening to. So that I don’t end up in the same situation when I end up having presentations recorded, I decided to look into getting an wireless microphone, but I quickly discovered that these are very expensive.

I thought about ways I could synchronize my iPhone audio recording with a video, when it occurred to me that there might be an application that allows my iPhone to act a wireless microphone, and sure enough, there is!

The name of the application is Pocket Audio, and it costs $1.99 (provided you already have an iPhone) which is obviously much more affordable than the three hundred dollars one can potentially spend on a good wireless microphone,.

To get the application working, you have to first download a copy of the server software for your computer (both Mac and a PC versions available) and install it on your computer. You may need to adjust your default sound options after doing this, as it seems that Pocket Audio wants to make itself the default audio input and output for your computer. You will also need to ensure that the firewall on your computer allows communication from Pocket Audio with the rest of your network. Now run the Pocket Audio server (called PocketControl) on your computer.

Next, you download the client software to your iPhone and start it up. It should automatically search for and connect to your Pocket audio server, and presumably if there is more than one available on your network, it should allow you to select which one you want to use.

Now whenever you use any program on your computer that has an option to select a microphone, you should be able to select your iPhone (called Senstic PocketAudio in the options) as an option. See an example of what this looks like below in the audio settings for Skype.

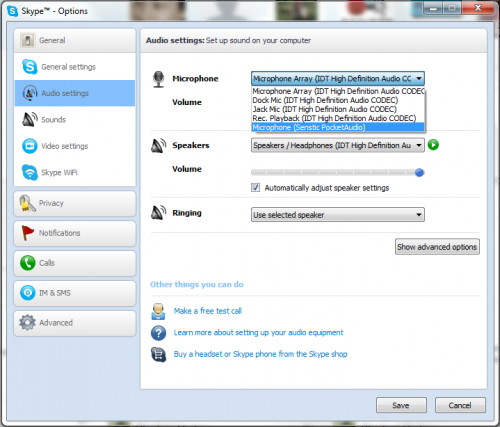
The audio quality was excellent, but there is a small delay, depending on your network. This is because instead of the audio being fed directly into your computer from an attached device, it needs to travel over your network. Still the small delay may be worth it to greatly increase your audio quality, and anything would be better than some of the sound quality I’ve seen in some recorded presentations.

Here’s a very short sample of the audio in a screen-recording I did. Note that I actually walked about 15 metres away from my computer, which is obviously not visible in the webcam embedded in the video below.

* This post was not paid for by anyone. I am just offering a solution to a problem that I had, and this seems like the best (and cheapest) option for me. I’m recording this solution here so that I remember it, should I need to use it again soon.

Bon Crowder shared this very interesting TED talk about some of the mathematics in movement and dance. I recommend reading her post to see some more resources on the mathematics of dance and movement.

Erik and Karl show some ways in which one can explore combinatorics, topology, symmetry, patterns in numbers, and fractions through movement.

An obvious question I have is, where else could we embed movement into mathematics?

• Students could count their steps while they move from classroom to classroom, or count steps as they climb them.
• A teacher could put a giant number line (or cartesian plane) on the floor of their classroom and students could practice arithmetic visually.
• Students could verify the Pythagorean theorem by counting steps as they walk along the legs and hypotenus of a large right-angled triangle on a playing field.
• When students all dance in a group, they could create tesselation patterns as they move across the dance floor in a group. They may need to see a video (shot from above) of themselves moving to see why this is interesting.

What are some other ways in which we could use movement activities to explore mathematical ideas?

I watched this video, and I was reminded of the primary reason I became a teacher. As a bullied youth, I wanted to try and help prevent this from happening to other children. I cannot see how I have been remotely successful in this goal.

I spend so much of my energy focusing on improving how my passion, mathematics, is taught, but not enough time thinking about and helping the kids who are my charges. I know that there are kids at my school who feel alone, and while they may not experience the intensity of the bullying that I did as a child, I’m sure their spirits are no less wounded than mine used to be.

Bullying is a complex problem. There are no simple solutions. That being said, children spend about 8 of their 16 waking hours involved in school in some fashion, and if at the end of this time they still feel isolated, alone, and broken, then we have failed utterly as an institution.

No one else has much time to influence their lives as we do. We need to make more of a difference.

Unfortunately we spend so much of our time and energy as an institution focusing on stuff which is almost trivial compared to some of the needs of our most vulnerable students. We know about Maslow’s hierarchy of needs, and while we cannot prove empirically that it has validity, we know from our experience that children cannot learn effectively unless they feel loved and love themselves.

• Schools should feel like communities where everyone knows everone else by name. It should not be possible for children to pass through our hallways and classrooms without talking to a single soul during the day,
   
• We should reframe the problem in the positive. Instead of "don’t be a bully" we should model and teach empathy and compassion,
   
• We need to start modeling empathy and compassion within our wider communities. We will never end bullying in schools while we accept it in the world outside of school,
   
• Compassion often develops from experience with the other. Instead of separating kids by age, we need to find ways to form connections between kids of different ages. This way younger children always have an older ally, even when they scared to talk to adults. We need inclusive classrooms, not just because it results in better outcomes for the children with special needs, but because it will help all of the children learn about their colleagues more deeply,
   
• We need to treat social interactions as a skill to be learned. When kids interact poorly, it is an opportunity for learning, and when kids are struggling, we should scaffold the skills they need both to cope and to understand their peers. One of my biggest problems growing up was that I did not understand the motivations and actions of the people around me, and so I often reacted poorly to even the smallest bit of negative attention. My nickname was Spaz instead of Porkchop.

Thank you, Shane, for reminding me of why I became an educator in the first place.

It is my experience that the more deeply I learn about a domain, the more questions I have. Similarly, when I know very little about something, I have lots of questions as well (although these are usually much different questions than the questions I have as I gain expertise). In the middle somewhere, the number of questions I have drops off as I mistakenly believe that I understand the domain better than I actually do.

Being able to ask questions about a domain is one of the ways one learns about it. So this diagram implies that a challenge in becoming an expert in a domain of knowledge is that eventually you know too much, and you run out of questions to ask, making learning more in that domain more challenging.

How can we encourage people to continue to ask questions as their expertise grows?

This afternoon my wife and I participated in my son’s student-led conference. In this conference, my son led us through a sample of various classroom activities he’s done over the course of the year. He was excited to share what he had done, and both my wife and I were very proud of him.

At one point, he was sharing a math activity he had done during the year. In this activity, the purpose was to add 5 and 7 by regrouping the sum into 10 and 2, using manipulatives. I remember my son saying, "Okay, so I don’t know what 5 and 7 is, so I’m going to count out 10 from 5 plus 7 and see what is left over and then add that to 10." He was obviously remembering instructions he had received on how to do addition using regrouping and counting.

The thing is, my son knows what 5 plus 7 is. I know he does. When we were driving home, I asked him what 5 plus 7 is, and he said, "Oh, I know that. 5 and 5 would be 10, so 5 plus 7 would be two more than that, so 12." In other words, he used a different explanation when talking to me about the problem, than when working in his classroom space. The context mattered.

In the classroom, he probably felt that he should use the method his teacher showed him. With me, he used the method he discovered himself (seriously, I never taught him any of the techniques he uses for addition, I just helped him develop a strong understanding of numbers) because that is what he feels comfortable with when he is around me and my wife.

It reminds me of the story Keith Devlin tells of street market arithmetic done by "uneducated boys of a poor background." When asked to do arithmetic in the context of their daily jobs as street merchants, the boys had sophisticated techniques they developed to reduce the difficulty of the arithmetic they would need to do. When asked to perform these exact same calculations in a different context, as word problems on pencil and paper, the boys failed miserably. The context mattered.

This complicates our understanding of what children know how to do because not only do we need to know what they can do when we are around, we need to understand what they can do in other contexts of their lives.

I read an interesting article recently about over-parenting, where children are made helpless because of too much support from their parents (and teachers). After I read the article, I remember this story from many years ago, shared by a colleague of mine.

"We had a kid whose mom used to dress him all the time, even though he was in sixth grade. She also used to feed him, and as a result, he didn’t know how to use a fork and spoon himself, which was a bit problematic at camp. Fortunately, he figured it out fairly quickly because there was no way we were going to literally spoon-feed him."

"One day, we were playing a relay race where one person would put on a shirt, run to the other side of the field, and pass the shirt to the next member of the team, who would put it on, and then ran back, and so on. When this kid’s turn came up, he ran to the other end of the field and raised his arms up, waiting for his teammate to put on the shirt for him."

This raises an important question for me; in what ways do we as teachers over-coach our students?

I have implemented some changes in my grade 12 math class in an effort to help build independence in my students, and the students at first feel a bit weird about these small changes, but then they adjust to them, and over time, they appear to become more independent.

1. I tell my senior students that they don’t need to ask me for permission to use the bathroom, they should just wait for a sensible time, and tell me where they are going. If I still taught middle school students, I would do this with them as well, and take the rare times when they abused the responsibility as opportunities to teach self-discipline.
    
2. I don’t assign specific problems from the textbook. I don’t even tell students where in the textbook the problems are (most of the time). If our students are unable to self-select challenging problems for themselves, and unable to find those problems in a textbook written for them in mind, then I certainly feel like we have failed them as educators.
    
3. I stopped answering all of their questions. Most of the time, I respond with a question, and try and move them toward being able to resolve all of the simple problems they run into on a daily basis.

(Image credit: Left – Multnomah County Library, Right: Sam Howzit)

If you ask people who attempt to predict the future of education, you will find out quickly that there are two very different, competing perspectives.

One camp believes that the future of education is in moving away from complete standardization of curriculum and focusing on nurturing students to become learners, so that when they need to learn something new, they are capable of doing so independently. They are less concerned with the media that students use to learn, and more concerned about ensuring that students have at least some say in what they learn, and how they learn it. They believe that computers are powerful devices for exploration, and that the full potential of computers in education has not yet been realized.

This first camp believes that learning is something best done within social contexts, while simultaneously believing that cultivating the ability to think independently of others is of critical importance in our life. They believe in students spending some time learning independently through self-exploration, and some time collaborating deeply with others. They believe in teaching kids how to think, not what to think. They believe the role of teachers is primarily to mentor students and to model being a learner with them.

The other camp believes that the future of education is in mechanical learning. They believe that if we can just find the right mixture of content, media, and machine-graded assessment, we can greatly reduce the costs of education, and deliver a personalized education experience to every child. They believe that a teacher’s job is to deliver content and assess the understanding of students, and they believe that these can both be done efficiently and effectively with a computer. They believe that if children just have the perfect explanation, they will learn.

This second camp believes that the future of learning is with children carefully isolated, sitting in cubicles, watching videos, and then answering questions prompted on the screen. They believe that social interaction with other children is at best a supplement to what happens on the computer, and at worst it is a distraction. This camp is usually more concerned with the cost of education than the quality of learning.

Both of my descriptions of these two camps are somewhat reductionist. Obviously there are shades of gray between these two camps. However, if you had to choose between these two visions, which would you choose? More importantly, what are you doing to make it a reality?