I’m working on a presentation on creating presentations.
What other advice would you offer?
Note: Open the speaker notes to view the image credits.
Education ∪ Math ∪ Technology
I’m working on a presentation on creating presentations.
What other advice would you offer?
Note: Open the speaker notes to view the image credits.
Whenever John (not his real name) entered my class, we had to open the windows. He smelled really bad, most of the time. He also wasn’t in class very often, and I never knew when he would be school, and when he wouldn’t be in school. There seemed to be no rhyme or reason to his attendance.
When John did attend class, he had to be given a new pencil and book in order to write down any notes or work any math problems. Eventually, I just kept a pencil and a notebook in class for him since he never did any homework.
He was an attentive and bright student, but he missed so many classes that he struggled to keep up. In fact, "keeping up" became impossible for John. When he wrote tests, he would do the questions nearly flawlessly that he had seen in class, but there were rarely enough of these kinds of problems for John to demonstrate mastery of the curriculum.
In about February of the year, John stopped coming to class, and I never found out what happened to him. I was talking to one of my colleagues about John, and she mentioned he was homeless, and I felt completely embarrassed that I never realized.
John is not alone. There were 1.6 million children in the United States in the year 2011 who experienced homelessness for at least part of the year. Many of these children struggle in school because of issues similar to what John experienced, and then continue to suffer throughout their lives in the vicious circle that is poverty.
I suggested to someone recently that we should build schools, especially in areas likely to be high risk, to be more like community centres, with access to health-care, food services, emergency shelters, social services, and after school care programs all under the same roof. Services for children could then be managed centrally by the school and the odds that a child could slip through the cracks and not get what they needed would be diminished. It would also be a lot less expensive than the current emergency-room health care system in the United States. The response of the person was basically along the lines of "It’s the parent’s fault. They need to be more involved."
To this I respond, we should not punish children for the periodic inability of their parents to make their lives work. If we are to be a humane society, then all children in our society should be cared for, whether or not their parents are always able to provide this care.
When you rely on a service, particularly a "free" (ad-supported services aren’t really free) service, you always run the risk that whomever is maintaining and controlling the service will shut it down, or strip it of functionality so as to make it less useful (or even useless) for you. This happened to Google Reader, it almost happened to Delicious, it happened to Posterous; this list will continue to grow over time.
The lesson for me here is not to rely on these third party servives, but take the time to maintain and control my own services. Right now, I maintain my own blog, my own online bookmarking site, and my own RSS reader. Running these services myself has been very easy as I have had minimal interruptions in the service of my website, and the code-base for these services is also under my control (so I can modify them as I need) since they are all open-source projects.
When OX Text is released, I am considering increasing the investment I put into my website (currently about $150 a year) so that I can consolodate all of the various projects I am maintaining onto one site, and migrate away from Google Docs. I just found Roundcube, which looks like it has the functionality I need to replace my current Gmail webmail.
I would like to migrate completely away from all services that are maintained by third party organizations because these organizations have a history of misusing the data I provide to them, and suspending support for products that do not meet the organization’s goals, regardless of the popularity of the product with their customers.
What other alternatives do you know about for popular services?
I’ve updated my presentation on social media, aimed at a parent audience (although I’m sure it could be used with educators just as easily). Embedded below. Note: The first few slides, up to slide 39, are intended to be shared fairly rapidly, to create a sense of overload in the viewer.
(Viewing this in your email or RSS reader? Try this link instead.)
In the not too distant future, there will no educational technologists. That is, there will eventually be no people who specialize primarily in teaching other people how to use technology. The reason why we have educational technologists now is that the rate of change of technology is so high that many people struggle to keep up with the changes, and so some of us have specialized in "keeping up with changes in technology."
The positions that will exist will be analogous to the role of librarians in schools, who do not primarily teach people how to operate books, they teach them how to read and utilize books (and other forms of text material) to learn about the world. In fact, it seems quite likely to me that librarians in the future will include at least a minor role in teaching others how to research using technology, and how to use and critically examine technology as a learning tool, in much the same way that many librarians do already.
Moore’s law, which famously states that the number of transistors on integrated circuits doubles every two years, may be more appropriately modelled with logistic growth rather than exponential growth. Logistic growth behaves very much like exponential growth initially, but as finite limits in resources or capacity are reached, growth slows down, and eventually levels off. It is very likely that instead of run-away technological growth and a singularity, that we will eventually reach a point where our hardware capabilities will remain somewhat stable, and when this happens, eventually software will follow suit. A strong benefit of software equilibrium is that bugs in code will be less frequent, and interoperability between different software will be easier to maintain, leading to technology which is much more reliable overall.
What this means is that the rate of change of technology will eventually slow, and people will have to devote less of their time to keep up with the changes, which means that being specialized in "keeping up with the changes" like educational technology people do, will be less of an advantage over others.
Another possibility is that technological change will not slow down, and that eventually there will just be people who have merged with the technology, and people who have chosen not to. In this case, educational technologists will be equally unimportant as the people who do not merge will be completely left behind by technology, and the others will not need our support. This kind of scenario is fairly dystopian from my point of view, so I prefer the first alternative.
A third possibility is that our ecosystem crashes completely, and our civilization follows soon after. In this case, we will not need educational technologists because we will be spending most of our time just trying to survive. Again, the first scenario for me is far preferable!
Given that equilibrium in software is likely to happen long after hardware equilibrium, our roles are probably safe for at least a couple of generations.
I’m working on a couple of short videos comparing the standard algorithm for a multiplication and addition, and considering some ways of using other algorithms which are more likely to make sense for students.
To be clear, these presentations do not enough justice to student-created algorithms, which I would strongly recommend as a starting place for exploration of algorithmic reasoning. These two videos are merely an attempt to compare two different algorithms against each other, and to provide some support for teachers interested in learning more about why we might want to use something other than the standard algorithms in our classrooms.
I also want to make it clear that how I am describing these distinctions in the videos is not how I would introduce them to children (or adults for that matter, if I have the time). Instead, I would start with setting up realistic situations, whole group, and small group discussions around investigating these operations, using both manipulatives and symbols to represent numbers in the algorithms. A really useful activity, for example, is for children to be making these comparisons themselves, so that they can look for patterns in different operations, and abstract these patterns into general rules they can follow to make their use of any algorithm easier.
I see these algorithms as a useful way to get started with abstract reasoning, provided they are framed in a certain way, as described below.
Multiplication
Addition:
Dave Cormier, in an excellent, excellent presentation, made the point that learning multiplication tables belongs to the "simple" domain of knowledge (which in his defense was probably an example he chose to help his audience understand the Cynefin framework). I think I need to understand his definition of simple better, because I do not see multiplication, especially when it is typically learned, as particularly simple.
I’m not trying to pick on Dave in particular, I have heard "multiplication is simple" from a lot of different sources, Dave’s presentation is just the most recent place. Look at the Cynefin framework below to get a sense of how Dave is classifying areas of knowledge.
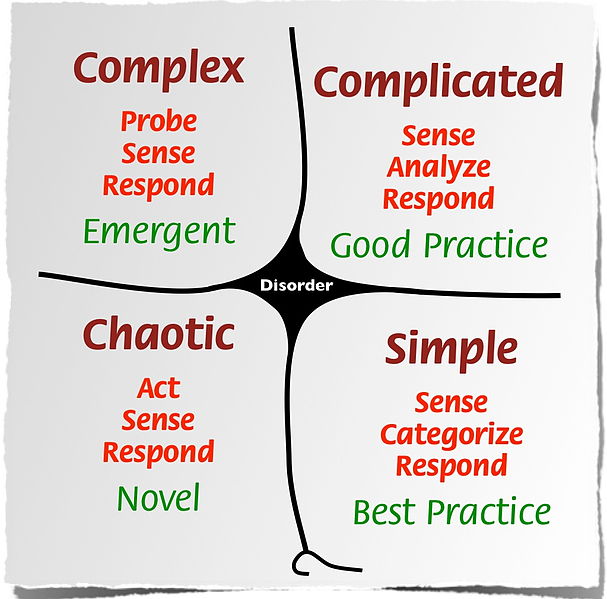
(Image credit: Dave Cormier)
I’m going to argue that multiplication as an area of knowledge more appropriately belongs to the complicated domain (especially for children).
First, the symbols used for multiplication (numbers) are a complex idea, and it is not entirely clear to me that every child really understands the relationship between numerals and numbers by the time they are introduced to multiplication. Numerals are a more complex topic than I think most people realize.
Here is some data to support this claim.

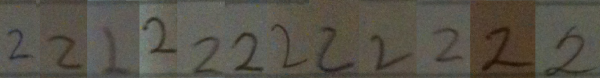
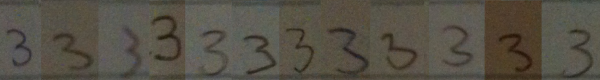


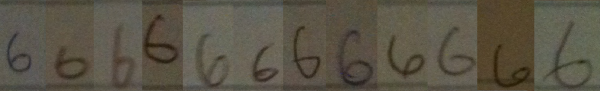
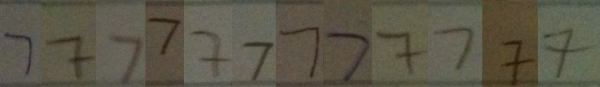

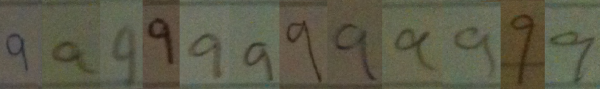
I went around my school and found 12 people (6 grade 11 students and 6 adults) to volunteer to write down the numbers from 1 to 10 in a row on a blank sticky note. I then took photographs of the sticky notes, and reorganized the numerals so that they were grouped by numeral type, rather than by person. It should hopefully be clear from these samples that when we teach students how to recognize numerals, we are really teaching them to recognize a class of objects which have similarities, but that there is no single way to write any numeral.
The idea of numbers themselves is complex. Different cultures may have different internal models for numbers, with some cultures being reported not to have an internal linear sense of numbers. It may even be that our sense of numbers doesn’t just vary at a cultural level, but at finer grain structures than entire cultures. Your sense of what numbers are is likely influenced by your parents, your local cultural, and our global cultural representations of numbers.
Multiplication itself exists in a culture, with different cultures viewing multiplication differently. There is currently no wide-spread agreement on whether multiplication is best represented with arrays, as repeated sums, as an area model, or as an algorithm used to calculate in these contexts. Given that mathematics educators do not all agree on something as fundamental to multiplication as how we define it, it hardly seems reasonable to call it simple.
Further, there are a large number of different algorithms for multiplying numbers, and many different possible representations. Some of these algorithms focus on mental arithmetic, others on visual representations, and others on numerical calculations. There are benefits and drawbacks to each of these methods, leading me to conclude that there is no, one best way to multiply numbers.
To top it all off, students, not all of whom even know how to tie their shoes, are expected to start mastering this skill and idea at age 8. I think that the idea of "simple" is a relative term. What might be simple for an adult might well be incredibly complicated for a child.