First watch this short video created by Dan Meyer so you understand the problem.
[WCYDWT] Coke v. Sprite from Dan Meyer on Vimeo.
I was having trouble wrapping my head around this problem. I saw people’s algebraic proofs, and I just felt there was something wrong with them. So I decided to construct a geomtric proof instead to make it more clear in my head.
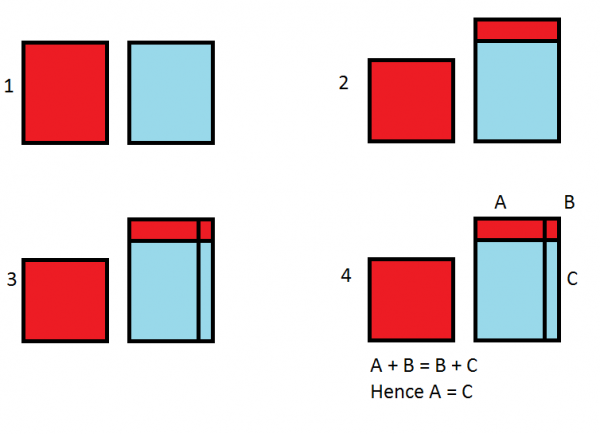
At step 1, both glasses have the same amount of liquid. At step 2, one glass has some liquid poured into the other glass. At step 3, we pour out the same amount of liquid from the right most glass, hence the area of the red rectangle is equal to the area of the vertical rectangle with the mixture of the two types of soda. Note that I’ve made sure to go the other direction in the diagram, so as to represent the fact that assuming the two liquids are mixed equally, essentially the soda I pour back is a mixture. In step 4, I note that area A + B is the same as B + C, because the two liquids are the same, and that the area of B is the same in both pictures, and so hence the area of A is the same as the area of C, which means that the amount of the first soda moved back and forth is the same.