Teaching to Big Ideas

On Big Mathematical Ideas, Cathy Fosnot writes:

 

Underlying these strategies are big ideas. Big ideas are “the central, organizing ideas of mathematics—principles that define mathematical order”(Schifter and Fosnot 1993, 35). Big ideas are deeply connected to the structures of mathematics. They are also characteristic of shifts in learners’ reasoning—shifts in perspective, in logic, in the mathematical relationships they set up. As such, they are connected to part-whole relations—to the structure of thought in general (Piaget 1977). In fact, that is why they are connected to the structures of mathematics. Through the centuries and across cultures as mathematical big ideas developed, the advances were often characterized by paradigmatic shifts in reasoning. That is because these structural shifts in thought characterize the learning process in general. Thus, these ideas are “big” because they are critical ideas in mathematics itself and because they are big leaps in the development of the structure of children’s reasoning. Some of the big ideas you will see children constructing as they work with the materials in this package are unitizing, compensation, and equivalence.

 

There are two pieces of evidence from cognitive science that support teaching to Big Ideas instead of teaching 180 discrete and perhaps haphazardly connected lessons.

 

1. It is much easier to remember ideas that are connected together in more complex schema.

 

This is why it takes many repetitions to remember meaningless information (like a string of randomly chosen numbers) and far fewer repetitions to remember meaningful information (like a poem).

Acronyms like SOHCAHTOA are far easier to remember than the three equations this acronym represents because the acronym provides some structure to the information to remember. The acronym allows us to chunk the information to remember into smaller, easier to manage pieces. The same principle applies to anything we want to remember.

I see Big Ideas as recursively being formed of many smaller ideas and that a Big Idea is a way of linking the smaller ideas together in the same way that the SOHCAHTOA acronym links together the words sine, cosine, tangent with opposite, adjacent, and hypotenuse.

 

2. It is much easier to remember information that we keep coming back to and are asked to repeatedly recall.

 

If I teach to Big Ideas, which may last more than a single session, the odds are greatly increased that the smaller ideas from which the Big Ideas are formed will be repeated across different learning sessions. This is critical because our brains are designed to forget information we don’t re-use and to remember information that is repeatedly helpful.

 
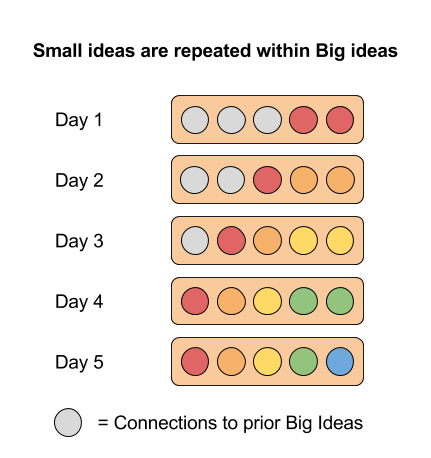
Suppose I want kids to remember Big Idea A, which is formed of smaller ideas A1, A2, A3, etc… and I teach this Big Idea over the course of a week. As I teach, I might ask kids to use idea A1 when working on idea A2, and then use ideas A1 and A2 while working on idea A3, all while asking kids to periodically attend to the relationships between A1, A2, and A3 as they are part of the Big Idea A itself. This means that during the course of a week, students may need to study idea A1 once, and recall idea A1 many times as they make connections to the other ideas of the week.

As the image also indicates, when teaching to Big Ideas means we can deliberately and explicitly make links between different Big Ideas, which means that across different weeks of instruction, the small ideas that make up Big Ideas can be referenced and repeated many times during the year. In our Algebra I course in our curriculum project, we don’t have a unit on graphing functions as graphing functions comes up in all seven units of Algebra I.

 

Here are some consequences of choosing to teach to Big Ideas instead of discrete small ideas:

1. You have to name both the Big Ideas and the small ideas from which they are formed.
2. Your curriculum can no longer be a collection of your favourite individual tasks as task selection and sequencing is far more critical.
3. Your lessons have to be designed to make the connections between big ideas explicit for children rather than implicit. A rich schema is unhelpful if it is woven invisibly into your curriculum.