If you or your students are going to talk about mathematical ideas in your class, it is critical that everyone understands the idea being discussed otherwise they are less likely to either remember it or be able to participate in the discussion.
Every time you or your students make logical leaps when explaining mathematical ideas, your students must fill those logical leaps with what they understand about mathematics or invent their own logic to fill the gaps.
Consider this task:
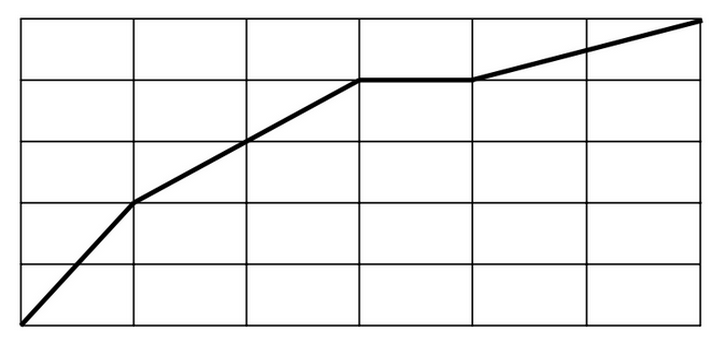
Which line segment is steepest? (source)
Make the task explicit
This task as currently written is actually ambiguous. There are a lot of vertical and horizontal line segments in this picture; are they meant to be included, or not? Are we only supposed to focus on the bold line segments?
We could change the prompt to something like “Which of the bold line segments is steepest?” This of course assumes that students understand what a line segment is and interpret bold to mean the same thing their teacher means. (It’s fine if students don’t completely understand what steepest means though so since the goal of a task like this is to come to a common definition of steepest.)
Use Gestures
Another approach is when asking students to solve the task, having it projected on a screen, and using one’s hand to trace and emphasize the line segments in the image, while asking the question.
Push for clarity
Now consider these (simulated) student strategies for solving this task and imagine students are describing their strategies out loud to share with the class.
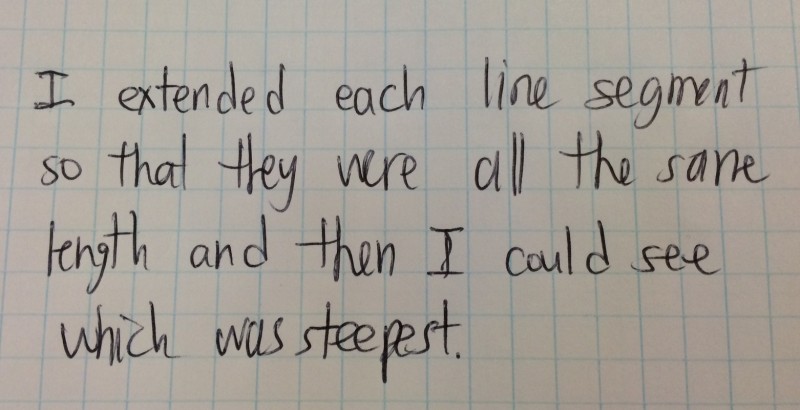
Student 1

Student 2
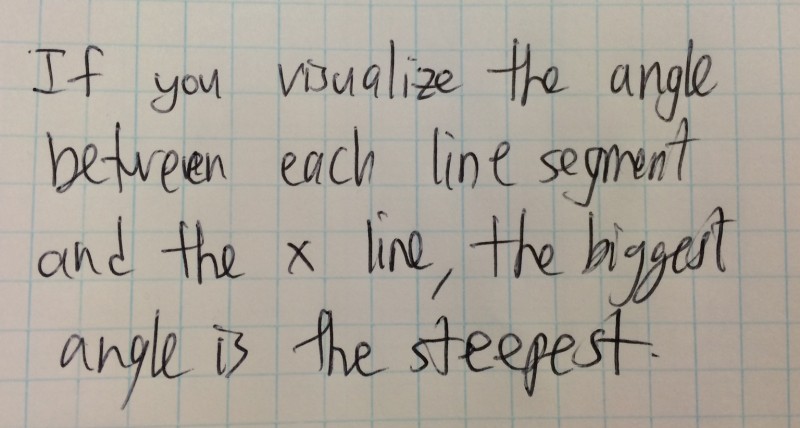
Student 3
If you have taught students how to interpret lines or line segments on a graph (or remember the mathematics associated with the task from when you learned it), you can probably figure out what these strategies mean. But there are gaps or missing steps in each explanation and since the explanations are out loud, there are ambiguities in each explanations as well.
With respect to the first strategy presented, what does it look like to extend all of these line segments so that they are the same length? How does the first student know that just because the line segments are now the same length, that one of them is steeper than another? And which line segment did they actually find to be steeper anyway?
In the second strategy, where are those little triangles drawn? Are they connected to the line segments in some way? And even if they are, one of the line segments is horizontal; how do I draw a triangle under that? Why does the largest rise over run correspond to the steepest line? Is that always true?
In the third strategy, where exactly are the angles between the line segments and the x-line? And what is an x-line? And why does the largest angle correspond to the steepest line segment?
Use questioning
One strategy is to ask clarifying questions about the strategy or to prompt students to ask clarifying questions of each other. In order to be able to ask critical questions “on the fly” it is extremely helpful to have anticipated the approaches students will use and at least some of the possible leaps in reasoning they may make, so that you can prepare questions in advance.
Use annotation
If you or students talk about mathematical ideas with no public written record of what was discussed, chances are high some students will either not be able to follow the argument being made or will quickly forget the argument. You can, and should, keep this record for students during discussions and use color and symbols to make the connections between mathematical ideas clear.
Here are some examples of annotations related to the student strategies above. Do these annotations make the ideas being discussed more clear? Is it more obvious why these strategies work?

Annotation for Strategy 1

Annotation for Strategy 2
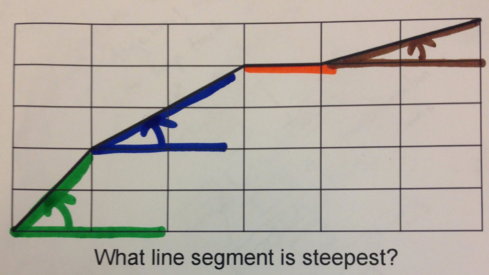
Annotation for Strategy 3
Keep a public record
Here is a record of what participants noticed and what their meta-reflections were when I used this task with them.
 What participants noticed |
 What participants reflected on |
Having this public record means that if a student’s attention wanders, they can get back into the flow of the class. It also means the information you want students to take away with them remains up for as long as possible. Further, when you move to prompting students to consider why the mathematical strategy works, students’ cognitive load around what the actual strategy being considered is decreased while there is a public record that they can access.
Prompt students to consider each others’ ideas
Unfortunately, usually when people (our students included) listen to each other they listen for what they expect to hear rather than what was actually said.
While it is worth saying that you should actively listen to what students say rather than changing its meaning or filling in the gaps in logic yourself, you will also want to use talk moves (like revoicing, restating, asking a student to restate, asking questions, wait time, etc…) to push your students to actively listen to each other as well.
Use independent think time
When we run professional development sessions, we virtually always incorporate a section on doing the math as this increases the odds that our teachers are able to have meaningful discussions about how to teach the mathematics. If students have already thought about a problem themselves, they will find it easier to understand someone else’s approach more easily.
What are other ways we can make the mathematics in our students’ strategies explicit while simultaneously respecting the thinking that students put into these strategies?
Samantha Malaquias says:
This is a great way to see how students think and get them to talk about their strategies with each other. Very different approaches. Thank you for sharing this!
March 30, 2016 — 5:13 pm
Gary Bass says:
Consider putting real world relevance embedded in the question..add values on the axes. Distance and time.
Then ask, “which segment represents the greatest speed?”
This creates several more methods of analysis..
April 1, 2016 — 9:36 am
Howard Phillips says:
Firstly, without any definition of the word “steepest” this task is missing the point. As it stands, even though in the original the words “Bike ride” were there, the absence of scales leaves one with just a picture, so why can it not be viewed from the side.
The mathematics in here is really about the meaning to be given to the word “steepest” as I am thinking of a line from top left to the point (1,0) on the non existent scales. After all, a steep hill is steep whether you are going up or down.
Regarding scales and meaning I would go further than Gary Bass, and ask “What, if anything, does this tell you about the bike ride?”. Then some math may come out of it.
April 3, 2016 — 4:55 pm
David Wees says:
And do you have any response to the rest of this post?
April 6, 2016 — 1:36 am
Howard Phillips says:
Yes, I liked the student responses. also the general move towards the “What do you see, notice, find interesting about…?” as a way to introduce new stuff. It does require a “stand back” attitude, which to many is unfamiliar. Maybe even with your example the first question could leave out the word “steepest”. Some might then say “Well, it looks like a graph but what of?”
April 21, 2016 — 2:17 pm