This summer I’ve been doing a lot of task-based curriculum development on a series of fairly short activities. We are trying to develop resources for use with an instructional activity created by Grace Kelemanik and Amy Lucenta called Contemplate then Calculate. A key part of this instructional activity is surfacing the kinds of things people notice that allow them to make mathematical connections and solve problems quickly and efficiently.
It turns out that Twitter is a really good medium for testing these activities because most people don’t have access to pencil and paper (a key component of Contemplate then Calculate) and there are a lot of people from a wide variety of backgrounds willing to try out the tasks.
What I do is first share the task on Twitter, kind of like so:
What is the value of the missing number? How do you know? What did you notice? #mathchat pic.twitter.com/Xltfxm8fpm
— David Wees (@davidwees) August 4, 2015
Then, I wait. Usually, I get a few responses right away and a few more responses over time.
Notice how I follow-up to those responses with questions to find out what people were thinking. If my objective with the task is to engineer opportunities for students to think about mathematics, it’s helpful to know in advance how they might think about any task I give them. A key benefit to Twitter is that a variety of different ways of thinking about the task emerge quickly and in many cases have led to me modifying the original tasks.
Some tasks get more responses than others. I try my best to respond to everyone who takes the time to try the question, but sometimes I miss people.
How many circles are in this shape? How do you know? What are all the ways you can figure this out? #mathchat pic.twitter.com/2p0neLZvhF
— David Wees (@davidwees) August 3, 2015
I also work to make sure that share back the work of the community back to the community.
@CDawson18 Contemplate then Calculate. Here’s the lesson plan: https://t.co/uUIEN4elbl and the slides: https://t.co/A1g5YzW9Uc
— David Wees (@davidwees) August 3, 2015
All of the tasks I’ve been working on, and so far we are up to about 30 of them with many dozens more in the pipe-line, are going to be shared, with a Creative Commons license, back to the math education community. Stay tuned for the URL.
Maya Quinn says:
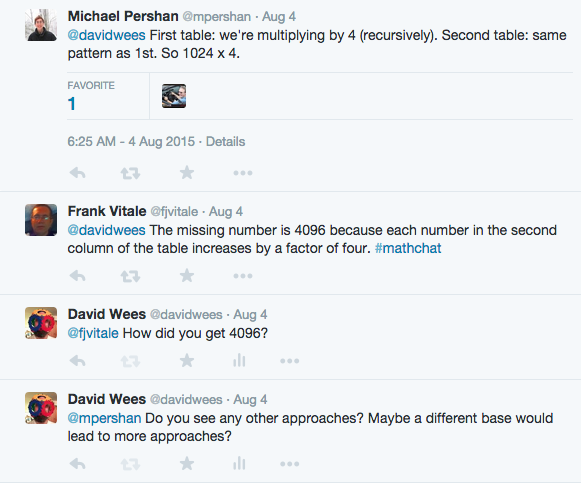
The two tables seem to differ by a factor of 4*4.
As in, 4^(x+2) = 4^x * 4*4.
So let us multiply the last entry in the left table, 256, by 4, and then multiply the result by 4 again.
256*4 = (250+6)4 = 1000+24, and
(1000+24)4 = 4000+96 = 4096.
Maybe 24*4 is not so easy to do in one’s head; well, 25*4 = 100, and then we can jump back 4 to land on 96.
Or maybe we learned the 12×12 times table, and we recall:
24*4 = 8*3*4 = 8*12 = 96.
It also seems that the numbers in the right table have units digits that alternate between 4 and 6. Maybe we could produce a sequence by lopping off that last digit:
1, 6, 25, 102, 409, …
I wonder, how might you continue such a sequence?
It looks a bit like the previous number is always multiplied by 4, and then there’s an alternating 2 or 1 added.
1.
1*4 + 2 = 6.
6*4 + 1 = 25.
25*4 + 2 = 102.
102*4 + 1 = 409.
So, perhaps the next term is:
409*4 + 2 = 1638.
Is it?
MQ
August 26, 2015 — 7:10 pm
David Wees says:
Hi Maya,
I really love your thinking. Based on the assumptions you made, all of your answer choices are possible. Clearly one has to be clear on what assumptions are being made for this question in order to solve it! Otherwise there are an infinite number of possible choices.
If both functions are meant to be exponential functions, which answer would you use? And do you have some ideas about alternate strategies people might use?
David
January 13, 2016 — 3:14 pm