Teaching proof

I’m currently working on creating a sample sequence of lessons for teachers to use for a geometry unit. At this stage, students will have been exposed to (but will not necessarily have learned all of) geometric transformations, constructions, and some review on geometric vocabulary.

My objective is to create a sequence of lessons which include:

• embedded formative assessment,
• opportunities for students to discuss student thinking,
• opportunities for students to make sense of the idea of proof,
• opportunities for students to prove geometric proofs,
• opportunities for students to engage in mathematical inquiry,
• engaging tasks that help get kids excited about mathematical arguments.

The last time I taught geometry, I think I maybe managed to to hit 1 or 2 points from this list, so I have given myself a tall challenge. I need help.

One of my university professors once told me, “Something is proven true when everyone stops arguing that it isn’t” so with that in mind, here is a vague idea that I am considering and need help fleshing out:

Basically, students would spend their time during this unit making interesting geometric observations and then attempting to prove to each other that these arguments are true. Part of their time would be exploring geometric objects, possibly through constructions and possibly through looking at (interactive?) diagrams. During this time, when they see something that they think might be true, they create a proof (in everyday language that they understand) that it is true, and then they present their argument, either in small groups or to the whole class.

Here is an example from my imagination. Suppose students have access to this online geometric construction tool (or lots of paper, a compass, and a straight edge) and when playing around, one of them creates this construction.

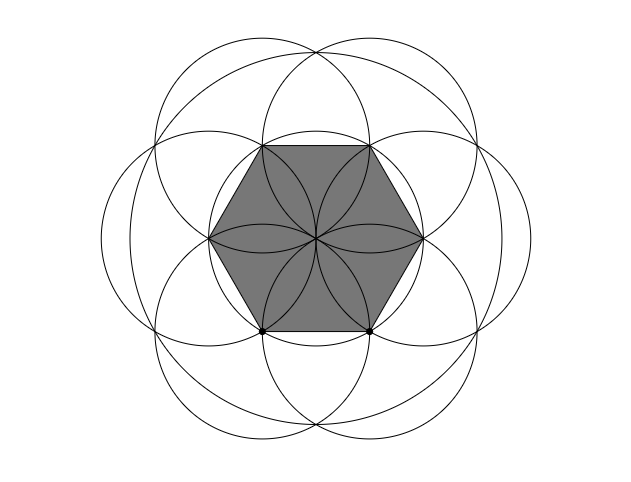
Student 1: “Oh wow, that’s pretty cool. I made a regular hexagon.”
Student 2: “It sure looks like a hexagon, but remember what Mr. Wees said? It might be just really close to a regular hexagon. How do we know for sure it is one?”
Student 1: “Hrmm. A regular hexagon has all the sides the same length, and this looks like all the sides are the same length, so it must be a hexagon.”
Student 3: “How do you know for sure the sides are all the same length?”
Student 4: “Yah, maybe they are like, one or two pixels off or something.”
Student 2: “How did you draw this? Can you show me how?”
Student 1 shows her group members how she came up with the construction. “See, it’s a regular hexagon.”
Student 3: “I notice that when you made each of the sides you used a circle.”
Student 4: “Yeah, I noticed that too.”
Student 2: “And all of the circles you used were the same size.”
Student 4: “Well, not all of them. There are bigger and smaller circles.”
Student 2: “Okay well all of the smaller circles are the same size.”
Student 1: “How do you know that?”
Student 2: “They all have the same radius, see? These two circles have the same radius, and these two, and these two. They are all connected so they all have the same radius.”
Student 4: “Ooooh, I have an idea…”
Student 1: “Me too! Those radiuses that he pointed out are the same as the lengths of the sides of the hexagon so if they are all the same, then all of the sides of the hexagon are the same size. Done!”
Student 3: “Is it possible to make a hexagon where all the sides are the same length, but the hexagon is still not a regular hexagon?”

 

Obviously this is an idealized situation, and maybe a bit unrealistic but this is where I would like students to end up. What kinds of classroom conditions would lead to students being able to do this? How would the class be structured? What kinds of supports would a teacher have to give to help support students?