Fractions are hard. Of course, I knew this before my lesson on Saturday, but the responses of my students to a task really drilled that point home for me.
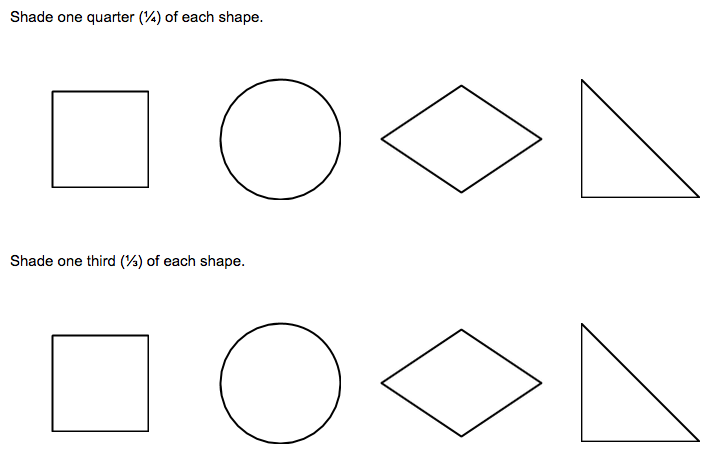
Here is the activity I gave my students to do:
Here’s what I anticipated they might do:
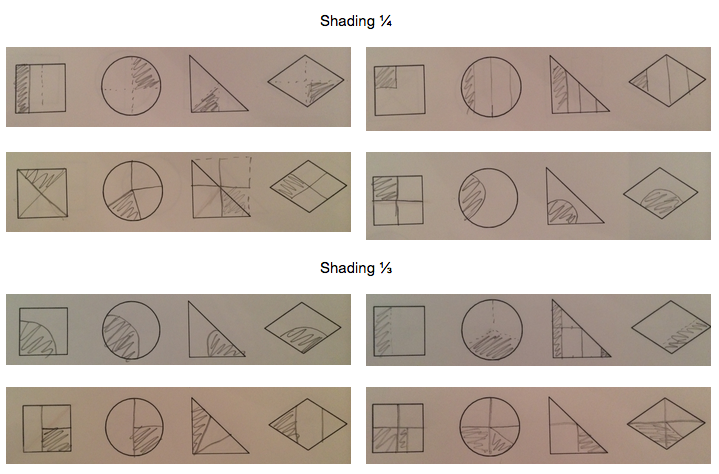
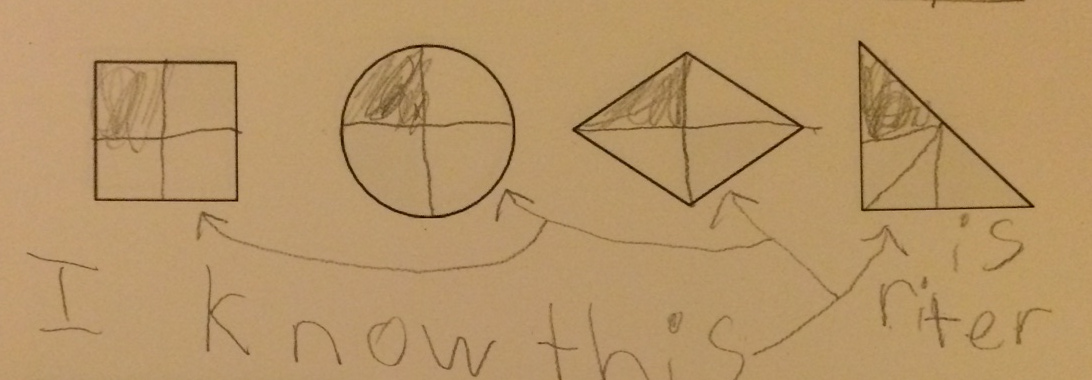
Here’s a sample of what they actually did:
This student seems to understand that if you want to shade 1/4 of something, you want to split it into four equal parts and then shade one of those parts. The triangle drawn is more challenging to divide, so the student likely estimated their partitioning of it.
However, if one wants to shade 1/3 of an object, it looks like this student thinks that they need to split the shape into four unequal parts and shade the smallest of those parts, maybe because they think that 1/3 is smaller than 1/4?
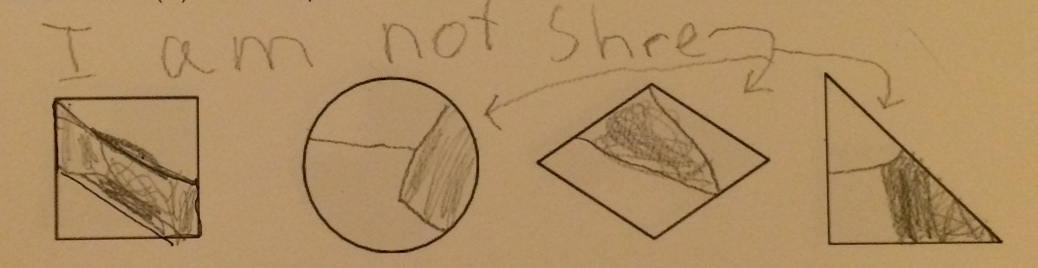
This student told me that they know that 1/4 is the same as “half of a half” and so they divided each of the shapes in half, and then divided one of those halves into a further half, and then shaded it.
When it came to shading 1/3 of a shape though, this student looks like they divided the shape into four equal parts and then shaded three of those parts. My guess is that they thought that fractions involve dividing into four parts, and then used the denominator of the fraction to choose how much to shade? I’m not sure that they noticed the inconsistency in this procedure and what they did in the first part.
This last student seems to have done pretty much the same as the second student, but seems aware that when you want to shade 1/3 of a shape, you want to first divide it into three equal parts and then shade one of those parts. I asked them about it and they said they just weren’t sure how to cut the shapes into three equal parts.
With this gap between what I was expecting to see and what I actually saw, I was left without knowing an effective way to respond. I decided that this task had little entry points for someone who really did not know what 1/4 and 1/3 meant (one of my student’s work was blank, which I am not showing since I do not have permission).
With the worry in the back of my head that I was probably reducing the cognitive demand for students, we split into two groups with my student-teacher leading one group and me leading the other group and we tried a different task, one which offered some context through which one might make sense of what 1/3 means.
“If you had a pizza and you wanted to share it equally with three people, how would you cut it up so that each person got 1/3 of the pizza?”
With this prompt, students in my group almost all produced work similar to the following:
With one student drawing this:
This second student, by the way, said that pizza comes cut into ten-slices and so the best we could hope to do is to give each person 3 slices of the 10 and then give away the last slice to someone else.
The knowledge that would have helped me better anticipate student understandings here is what I call “the ways children typically understand mathematical ideas” and is the kind of knowledge that is rarely explicitly taught before starting teaching. Every time I teach a new topic, I notice that the ways students think about the ideas are different than what I expect, and over time, I learn to anticipate student thinking better as I get feedback from working with them.
If you had students showing these kinds of responses to this task, what would you do during your next lesson on fractions to support them?


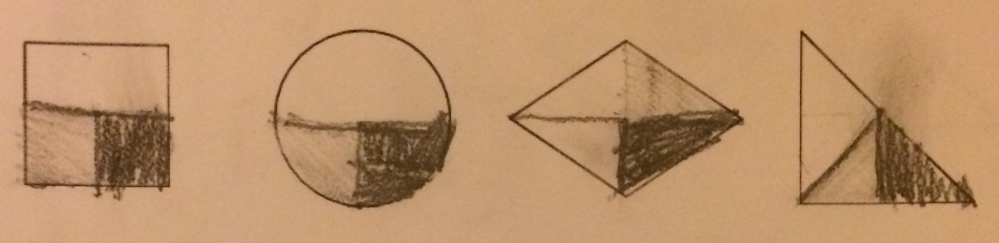
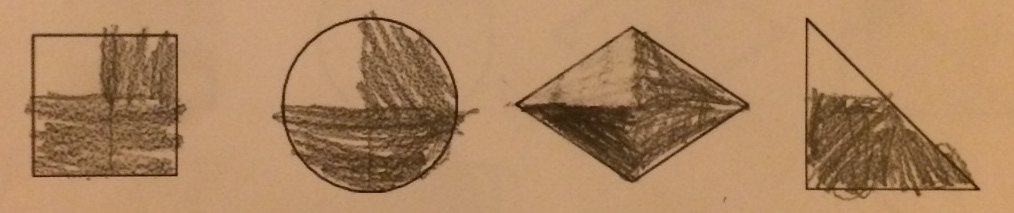
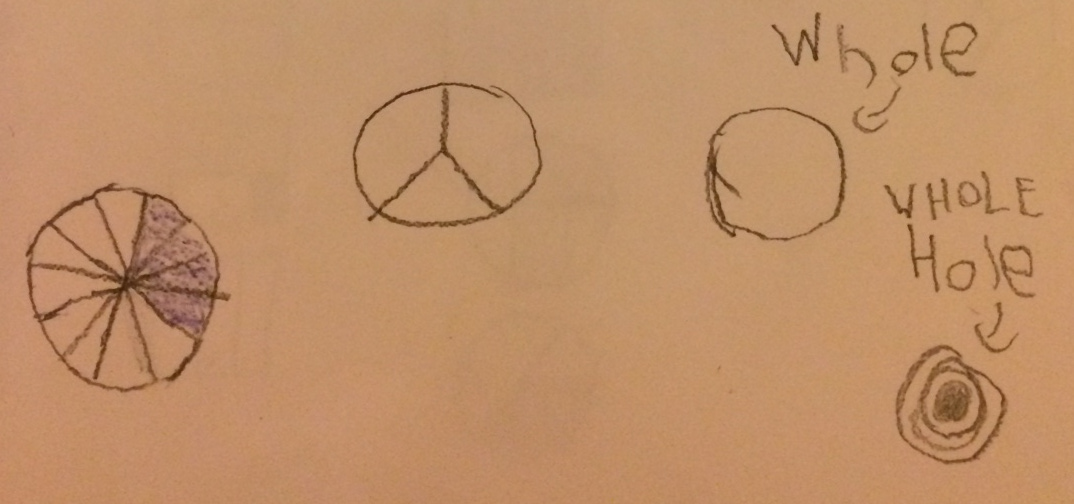

Marilyn Burns says:
Here’s an idea that might be useful for a fraction lesson with these students. It’s based on an idea for a very different lesson created by Malcolm Swan (from the Shell Centre in Nottingham England). The specific lesson from Malcolm that inspired me to think about your fraction lesson is about algebraic expressions. The link describes that lesson and has videos of students working. Here’s how I think that lesson might be changed to focus on fractions.
Make several sets of 3-by-5-inch index cards or 3-by-3-inch sticky notes.
Set A: Three cards with the fractions on them: 1/2, 1/3, 1/4. (I suggest putting 1/2 in there since it’s generally more accessible for students and an important building block.)
Set B: Shapes as you drew already divided and shaded to show the fractional parts in different ways. I think it’s important to show each fraction illustrated in more than one way, both with different shapes and on the same shape.
Set C: The fractions named in words: one-half, one-third, one-fourth.
Set D: More of Set B type cards for the same fractions for groups that finish more quickly.
Set E: The same fractions now illustrated with sets of objects; e.g., 6 oranges with 3 circled or shaded.
I’d have students work in groups of 2, 3 or 4. I’d give each a sets A and B first and ask them to set out the fraction cards, one underneath the other, and then place each of the shapes cards next to the fraction it matches. Also I’d tell them to make a separate row of all the shapes that they didn’t think match any of the fractions. (Hmmm, maybe include shaded shapes that really didn’t fit? Or not?)
If they pasted the cards on a large poster, they could compare with other groups. As groups finished and I wanted others to have more time, I’d give Sets C and D, and maybe even Set E for a group that needed even more. This is a way to differentiate the experience while buying time.
When groups claim to be finished, I’d check their work before giving another set of cards. That pushes me to think about hints when there are errors or when students are stuck. (I’ve been following Michael Pershan’s hint quest.) What makes sense to me are general hints such as:
I see one shape next to 1/3 that doesn’t belong.
I see shapes in your “extra” row that match fractions.
I haven’t thought this through much, but I’m working these days on fractions with fifth graders and am sort of obsessed with fractions. I have a blog post in the works about my recent experience, but I’m also in the middle of another blog post about multiplication in grade 3, which I’ll get done first. Stay tuned.
Thanks,
Marilyn
May 3, 2015 — 8:41 pm
Tom says:
Isn’t it amazing how pizza brings things into sharper focus?
I always used to teach fractions from a basis of cake. It’s amazing how far you can get through fractions-relevant parts of the curriculum just using cake (my top set GCSE students would often head back to cake when dealing with algebraic fractions). Students would often say things like “hey, this would work for pizza too!” and then someone would come up with a way of using it to work with rectangular cakes, and then with smarties on top of the cake, then very soon they’ve generalised it and all you have to do is neaten it up a bit with them so that they’ve got the notation sorted.
A student once made a cake for my birthday and insisted on sharing it with the whole class during the lesson. When the principal turned up I ad-libbed a cake fractions activity… I think I got away with it.
May 3, 2015 — 10:15 pm
Tyler says:
David and Marilyn,
Thanks for sharing all of these ideas. Marilyn, like you, I am up to my eyeballs in fractions right now from my work with fifth graders. I have been spending so much time thinking about them I am seeing them everywhere!
I think Marilyn’s lesson idea would be helpful because it would give students a chance to confer with one another and provide some opportunities for self- or group-correction as they work. As you saw, there were lots of misconceptions apparent in students’ work on your worksheet, but they weren’t able to learn from each other as they likely would in Marilyn’s activity.
It is hard to know in some cases whether the misconceptions are in how to divide up the figures or in what the given fractions represent (or both!). If you were to do this again, you may want to add a prompt after each part that asks something like, “How do you know that your shaded area represents 1/4?” That might give you additional insight for the students who you are unable to follow up with and could prompt others to reflect on how they know what 1/4 is.
Tyler
May 3, 2015 — 10:20 pm
Elham Kazemi says:
The difference between a fourth and a third in students 1, 2 and 3 are fascinating. Do you have more information about what they were thinking when they tried to represent 1/3? I’m not sure how old your students are and if they have had a lot of fractions instruction or are new to the ideas. I’d love to hear about what they were trying to draw and why they think their drawings show 1/4 or 1/3. I’m curious about your idea that student 2 made 4 parts and shaded the smallest of those parts to show 1/3. Wondered if that is indeed how student 2 thought about it. I love what student 2 said about how he/she understands what a fourth is. The fair sharing contexts have been really helpful for our work starting with 2nd and 3rd graders about partitioning and what to call the size of the piece. I’ve learned from Empson and Levi to start there and use words to describe shares before introducing notation.
Love this post David and learning from the students.
elham
May 4, 2015 — 1:41 am
Lisa Soltani says:
I wonder what your students would have done with 1/3 if you had just given them a skinny rectangle to shade, bar model style. Or was there something about the pizza context that helped? It seems to me what you are asking students to do here is two things: 1) to generalize their understanding about 1/4 and 1/3 and apply their understanding to different figures, and 2) to do some spatial reasoning around decomposing different geometric shapes. I agree, it’s hard.
May 4, 2015 — 2:23 am
David Wees says:
Marilyn,
I’m working on the task design you suggest. I think the most challenging part will be Cards B and E obviously. I’ve got a draft of some ideas for the shaded fractions which I will share tomorrow. I’m not clear that I should lead with this activity. Based on Elham’s comment, I’m wondering if students need more experience discussing and describing sharing things.
Tyler,
I almost always have my students work on tasks independently and then in pairs or small groups. The work shown here is the result of the individual work. The pair work looks a fair bit different, but until I have more individual work, I don’t really know what individual students might produce. I do have reflections that I asked them to write about this, but I found them mostly confusing to read. I need to follow up with the students more.
Elham,
My students are aged 8 through 11 but they are almost all (all but one) home-schooled and so their exposure to things like fractions varies more than you might expect given their age. All of the students, aside from one, have used the word fraction in conversations and discussions. I think that your curiosity about what students were thinking suggests an action I can take; I can confer with some of these students and find out more about their thinking. I’m also now curious about the sharing. When I gave the pizza example and had them think about how to share it, three of the students in my small group immediately had some ideas about how to do that, as represented by the 2nd to last photo above.
Lisa,
I didn’t include this in the post, but in the previous lesson I basically did what you suggested for one-quarter and almost all of my students were able to do that, leading me to wonder what they would do if I removed the supports. I have not however offered any scaffolded examples for 1/3. You are right, the decomposing of the shapes might be best taught separately which is part of the reason I like Marilyn’s suggestion; it does the decomposing of the shape for students.
May 4, 2015 — 2:34 am
Paul Rehmet says:
Fractions are hard! You may want to try an interactive tool I am creating to help students understand fractions. Using a pie to visualize a fraction, it encourages students to change the numerator or denominator of the given fraction to see how it changes the size of the pie slice. Students often get an “aha” moment when they increase the denominator of a fraction and see the number of pie slices increase yet the size of each slice decrease. I would love to know if you find this helpful, it may encourage me to finish it! http://www.mathmagi.com/fraction-fred.html
May 6, 2015 — 1:06 am
Leia says:
I think I’d give them the same shapes but with dividing lines already drawn (into 1/12s perhaps so it works for both) to try and pin down whether the problems are to do with dividing shapes or basic understanding.
May 6, 2015 — 10:31 am
David Wees says:
Some clarification points about my blog.
1. I don’t post comments that are advertisements thinly veiled as advise.
2. I don’t post comments that are insulting to me or to other people on this thread.
3. I am very clear what fractions are and what they are not, my post title does not mean I find fractions hard, it means that they are a concept children find hard and that the ways they are introduced should be more deliberate than what I attempted in the lesson described above.
May 7, 2015 — 1:01 am
Rebecca Kesler says:
What if you started in the place of asking them to tell you what they know about fractions? I envision this happening in groups of 2,3, or 4 on a large piece of paper and then sharing out. Encourage the students to write fractions, draw pictures of them, think about and record places they’ve used them or seen them. Groups could then discuss what others have shared–Are they fractions? What do they mean? This would give you a deeper understanding of the range of knowledge in the class, and certainly they would learn from each other. Just a thought.
August 9, 2015 — 3:41 am
David Wees says:
I like this as a starting activity for the unit. I’m only wondering how to structure this so that everyone has an opportunity to share to their group. Maybe start this off as an individual activity, then have students work in small groups to produce the poster (while I circulate and find out how the students understand fractions), and then share a summary of the ideas with the entire classroom?
August 9, 2015 — 11:23 am
Fraction Solver says:
For me, learning fractions through visualization is the best method because I can easily picture out what is the meaning of fraction. Also, this kind of method is like learning through actual experience because actual experience means you see, feel, or all your senses are used.
January 13, 2020 — 1:17 pm