Month: October 2019 (page 1 of 1)

Here is a video of Siegfried Engelmann demonstrating the mathematical learning of some children he worked with for a period of 1 or 2 years. Engelmann is one of the co-developers of a program called Direct Instruction, not to be confused with its cousin, direct instruction.

At the beginning of this video, Engelmann is careful to frame the video as a demonstration of learning rather than a demonstration of teaching, but it actually ends up being both. Engelmann, being a caring educator, cannot help but do a bit of teaching in this video.

 

 

Lesson analysis:

First, Engelmann builds up student motivation by presenting problems as challenging. He sets up students with statements like, “That’s pretty good, but pretty easy! Wait til you see this one.” When a student responds with a correct answer, he responds with, “Yay!” and then asks everyone to repeat the question and the answer. This kind of interaction is an ongoing theme throughout the video.

The students do not raise their hands, nor does Engelmann call on any students individually. Instead students call out answers as soon as they have them, so that often many different students call out answers together.

Next, Engelmann chooses specific sequences of problems to ask or pairs of problems that make some idea more clear through their variation from each other. For example, here is one sequence of questions:

1. What’s 8 plus 2?
2. What’s 10 plus 2?
3. 12 plus 2?

And here’s another sequence:

1. 7 plus 2?
2. 7 plus 3?
3. 7 plus 4?
4. 7 plus 5?

Choosing a sequence of problems to answer to elicit a particular strategy or idea is a reasonably common strategy in teaching, sometimes called a Number String or Problem String.

After nearly every question, the students respond by repeating the question and answer in unison, something they have clearly been taught to do. Underlying this strategy is presumably the belief that all children should be expected to participate in some way in class. Doug Lemov would call this, No Opt Out, and others have referred to it as holding high expectations for students.

Engelmann also circles back to previous problems students have done, increasing the connections students might make between problems. About 1 minute after students solved the problem “7 + 4 = ?” verbally, Engelmann writes the following on the board for students to solve.

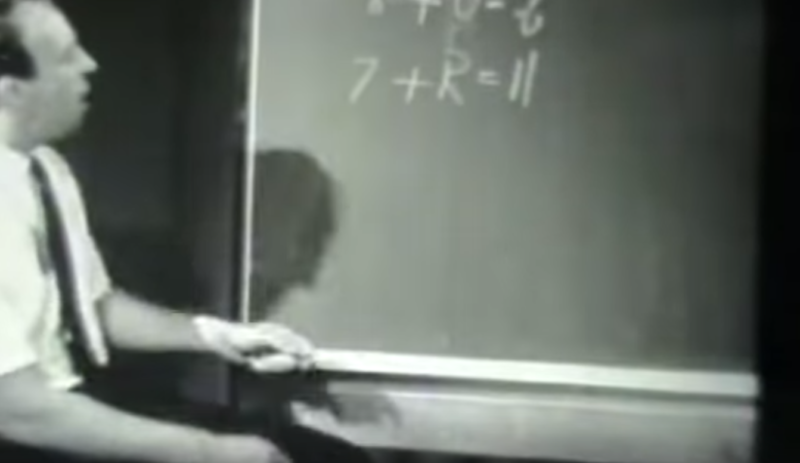
While Engelmann does not make the connection between this problem and the one students solved earlier explicit, it’s not likely to be an accidental choice of problem, given how deliberately the problems appear to be selected through-out the video.

Students frequently can be seen to be counting to find the answers to the question, a practice Engelmann makes no effort discourage, in fact he prompts it as a strategy at one point during the video.

Throughout the video, the children are exuberant and excited to be participating in this lesson. I did not notice any times when children seemed “off task” or disruptive, except perhaps towards the very end of the session where some of the children appear a bit tired.

At one point Engelmann makes a deliberate mistake, a common strategy used by teachers, and three of the children run up from their seats to correct the mistake for him, which ends up being part of the fun of the lesson. He also models how he responds to making a mistake and being corrected by the students — it’s no big deal.

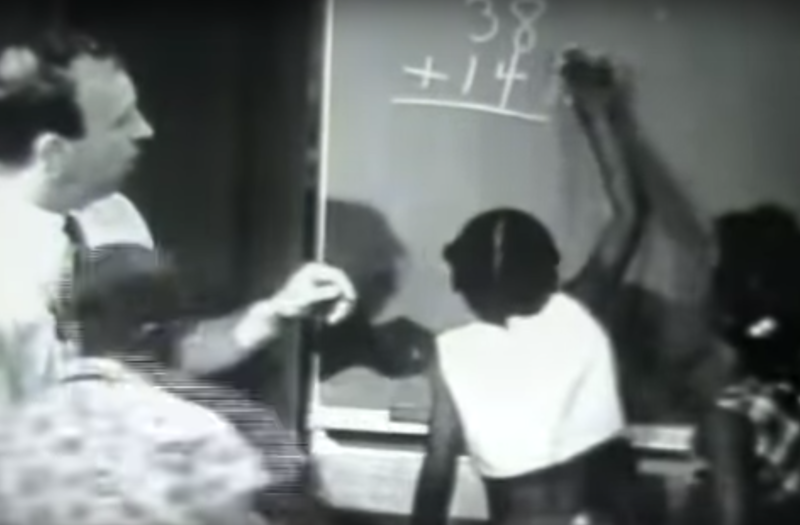
Engelmann pays careful attention to the language he uses. There are no tricks, no shortcuts, and no mathematical imprecisions. For example, in working through the example of 38 + 14, he is careful to refer to each digit by its place value meaning, so instead of saying 3 plus 1, he says 30 plus 10.

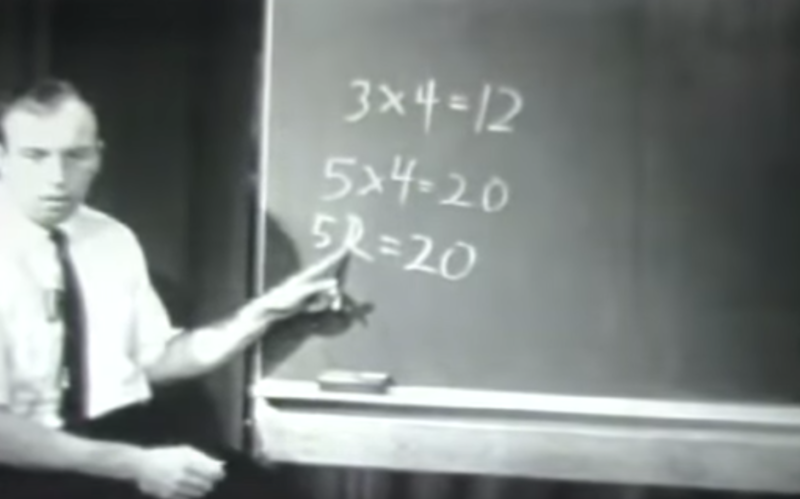
Engelmann asks many questions during the lesson. At one point, he asks, “Why can’t I erase the R here and put a 4?” which is likely intended to highlight the distinction between 54 and 5 × 4. Notice how he has both examples visible for contrast and that he is using an iconic gesture to emphasis what he is talking about with his question.

At one point, Engelmann draws a rectangle and marks it 3′ by 7′ and then asks students, “How many squares would be in this shape?” One of the student starts thinking out loud and says, “Okay, count by 3s. Count by 3s seven times.” The next problem he writes up he uses the same rectangle and relabels the sides 4 and c and marks the area as 24. He then asks students to figure out what c must be.

Two of the students call out 5, then another student calls out 6. Engelmann responds with, “Is that right?” as the students say 5 and then “6 is right!” when a student says 6. Engelmann then prompts students to “count by 4s how many times to get 24” as other students join him and repeat his instructions. As a group then, the whole class counts by 4. No students are singled out when they make mistakes, but no mistakes go without feedback either.

Near the end of the learning demonstration, Engelmann gives a fairly challenging problem.

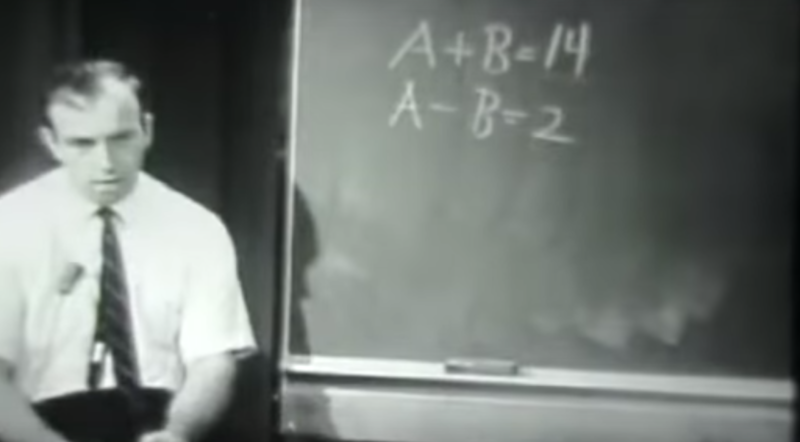
Engelmann waits 20 seconds before taking any action other than just watching the children think. Instead of telling students the answer or giving them a strategy, he changes the problem.

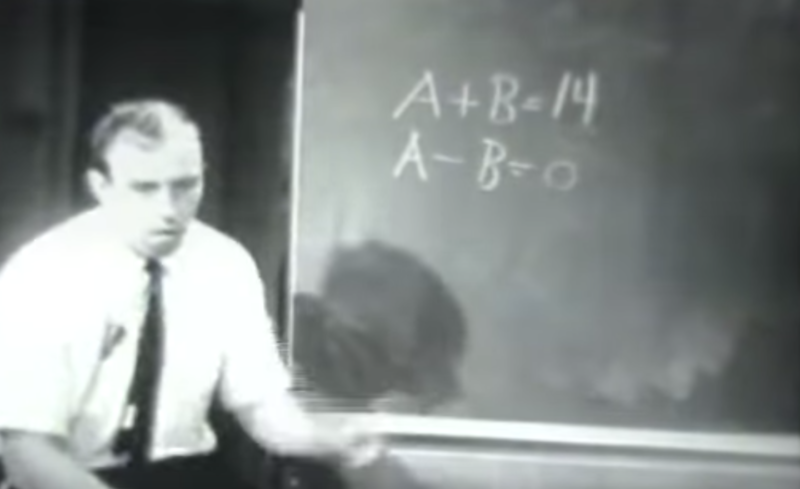
Students figure out the revised problem, and then Engelmann puts the original problem back up on the blackboard. He then waits again, this time for 18 seconds. This amount of wait time is remarkable given that most of the evening, Engelmann usually never waits more than a second for students to respond. Finally a student responds, and Engelmann congratulations the student and shares their answer with the class.

The class ends by Engelmann thanking the students for their participation and shaking each students’ hands.

 

Additional observations:

• Engelmann makes very little use of representations other than the symbolic although the students use their fingers as a tool many times.
• During the video Engelmann does not tell students exactly how to solve any of the problems, although he is fairly leading in one instance. It may be that this prohibition exists to make it easier to demonstrate the learning of the students and it may also be that explicit explanations are actually rare in his teaching.
• The pace is fast and variety of different arithmetic topics demonstrated through out the session is fairly large, but most of the numbers Engelmann uses are single or double digit numbers that students can still count with. The bulk of the mathematical work is on thinking about addition and subtraction in various ways with multiplicative ideas coming up as “counting by groups” or repeated addition.
• Engelmann makes use of a number of strategies also recommended for teachers to use with inquiry-oriented instructional routines suggesting that these strategies may be lesson-type agnostic.

 

Watching this lesson was a very different experience for me than most of the direct instruction I have observed. In fact, the experience was so different for me as to leave me unsure what relationship, if any, exists between typical direct instruction and what was intended by Engelmann as direct instruction?

Here’s a video of my son practicing at the playground. Prior to this, my son had already spent about five minutes trying to accomplish the same task.

 

I have two questions now after seeing my son practicing at the playground:

• How is this practice different than what practice typically looks like in math class?
• How can we make practice in a math class more like practice at a playground?

Children think with their minds, not with their hands. So when we assign activities because they are “hands on” it is more appropriate to think of these activities as being “minds on”. But of course, our minds are always on (to some degree) so now we want to specify, what exactly is it that is different about this task and what do I hope children will learn from this activity that they cannot learn without this activity?¹ Or alternatively, what does this activity allow that another activity might not?

For example, giving kids algebra tiles doesn’t mean that they will learn something important from using those algebra tiles. They might, but they might also learn the same thing from a structured activity using the area model.

My experience is that when I have vague hope that children will learn something from an activity that is related to the mathematics I want them to learn, they usually don’t.

To be clear, I see nothing wrong with students playing with manipulatives when free play is the goal. Sometimes having vague goals and experimenting with the use of manipulatives as a teacher is a good starting place for thinking about learning, but we should not conflate the ability of manipulatives to support learning with the actual learning students do as a result of using them.

 

References: